Магнитное поле тороида, соленоида

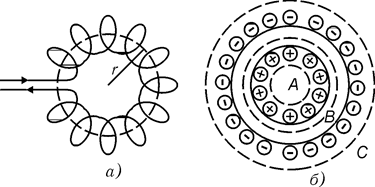Рис. 17.8

Тороид – это "бублик", на который намотан металлический провод (рис. 17.8, а). Обозначим N – общее число витков; r – радиус средней линии тороида; I – сила тока. Рассчитаем магнитное поле, создаваемое тороидом в точках A, B и C (рис. 17.8, б).

Точка A. выберем замкнутый контур в виде окружности, проходящей через точку A. Поскольку внутри выбранного контура токов нет, то правая часть в (17.28) равна нулю и, следовательно, в этой точке B=0.

Точка C. Как и в предыдущем случае, выберем замкнутый контур в виде окружности, проходящей через точку C. Правая часть в (17.28) в этом случае равна NI-NI=0. Таким образом, на основании (17.28) получаем, что в точке C B=0.

Точка B. Снова выберем замкнутый контур в виде окружности, совпадающей со средней линией тороида. Контур охватывает N токов одинакового направления, поэтому правая часть в (17.28)

.

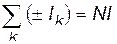(17.30)

Из соображений симметрии можно заключить, что в любой точке средней линии тороида магнитная индукция направлена по касательной к этой линии и всюду одинакова по модулю. Поэтому

.

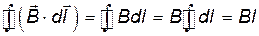(17.31)

Подставим (17.30) и (17.31) в (17.28):

.

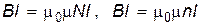(17.32)

где 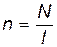– число витков на единицу длины тороида.

Соленоид можно представить как тороид бесконечно большого радиуса. Магнитное поле тороида не зависит от его радиуса, поэтому вектор магнитной индукции внутри соленоида может быть найден по той же формуле (17.32), что и для тороида. Линии индукции внутри соленоида параллельны друг другу, а числовые значения вектора всюду одинаковы, поэтому магнитное поле внутри соленоида является однородным. Однако, следует отметить, что вблизи от начала и конца соленоида магнитное поле не будет однородным.

Дата добавления: 2015-06-04