Аналитическим способом

Определение площадей

ПО ТОПОГРАФИЧЕСКИМ КАРТАМ И ПЛАНАМ

ОПРЕДЕЛЕНИЕ ПЛОЩАДЕЙ

ПО ГОРИЗОНТАЛЯМ

ПОСТРОЕНИЕ ПРОФИЛЕЙ МЕСТНОСТИ

Для построения профиля по заданному направлению на карте соединяют точки прямой линией и определяют отметки всех точек пересечения этой прямой с горизонталями, а также конечных точек и точек перегибов местности (см. с. 50 – 53, разд. 3.4.2.5. и рис.30).

Затем на миллиметровой или в клетку бумаге проводят две взаимно перпендикулярные линии – оси. На горизонтальной оси отмечают исходную точку, и от неё в масштабе данной карты откладывают расстояния до всех остальных точек. Для ускорения работ нужно приложить полоску бумаги к заданному на карте направлению и перенести на неё взаимное положение всех отмеченных точек прямой. После этого полоску бумаги прикладывают к горизонтальной оси и переносят отмеченные точки на миллиметровку. Рядом с точками подписывают их отметки. Далее в отмеченных точках восстанавливают перпендикуляры к горизонтальной оси, вдоль которых откладывают величины отметок в заданном масштабе. Чтобы профиль не выходил за пределы чертежа, горизонтальную ось принимают не за уровень моря с отметкой 0 м, а за некоторый условный горизонт, отметка которого будет равна числу, меньшему минимальной отметки поверхности Земли на данном участке и кратному сечению рельефа h_c. Для упрощения работы рядом с перпендикуляром в точке А построить шкалу высот. Для этого от условного горизонта вверх в заданном масштабе откладывают отрезки, кратные сечению рельефа и рядом с полученными точками подписывают их отметки. После этого по направлению каждого перпендикуляра необходимо подняться на уровень, соответствующий отметке данной точки горизонтальной оси, и отметить искомую точку профиля. Полученные точки соединяют ломаной линией. Для конечных точек и точек перегиба местности, где отметки не являются числами, кратными сечению рельефа, следует подниматься на уровень, который определяется путём интерполирования между соседними отметками горизонтальных линий.

В настоящее время определение площадей по картам и планам находит всё большее применение в связи с введением в стране земельного и городского кадастра.

Определение площадей участков местности по топографическим картам и планам может производиться тремя способами: аналитическим, графоаналитическим и механическим. Каждый из этих способов имеет свои достоинства и недостатки.

В тех случаях, когда замкнутый контур представляет собой многоугольник, координаты вершин которого будут вычислены при решении прямой геодезической задачи, например, при создании съёмочного обоснования в виде замкнутого теодолитного хода, или измерены по карте или плану (см. с. 55, разд. 4.2. “Определение прямоугольных координат”), площадь его может быть вычислена аналитическим способом (рис. 36)

Х

У₂ 2

а

с У₁ 1

Х₂

Х₁

в

У₃ 3

Х₃

У

Рис. 36. Схема определения площади аналитическим способом

Действительно, анализ рис.36 показывает, что площадь треугольника 1,2,3 будет равна площади прямоугольника а23в минус площади трапеций а21с и с13в. Распространяя этот анализ на многоугольник с любым количеством вершин, можно утверждать, что двойная площадь многоугольника будет равна сумме произведений абсцисс всех вершин на разность ординат последующей и предыдущей вершин

S_мн = 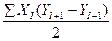. (44)

Площадь многоугольника может быть вычислена и по преобразованной формуле, где двойная площадь данного участкаместности будет равна сумме произведений ординат всех вершин на разность абсцисс предыдущей и последующей точек

S_мн =. 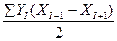(45)

С целью контроля вычислительных работ площадь многоугольника определяется по обеим формулам.

Аналитический способ даёт более точные результаты, чем другие, если даже измерять координаты графическим путём по карте или плану. Однако во втором случае возрастает его трудоёмкость, так как точно вписать многоугольник в криволинейный контур практически невозможно и приходится прибегать к некоторым обобщениям в его конфигурации, что приводит к резкому снижению точности результатов. Поэтому при определении площадей очень извилистых контуров, иногда целесообразнее использовать более простые способы, например, графоаналитический.

Дата добавления: 2015-06-04