И водохранилищ

Наличие горизонталей на топографических картах и планах позволяет решать и такие задачи, как определение объёмов земляных работ и водохранилищ, выполнять вертикальные планировки на строительных площадках.

Объём земляных масс и водохранилищ может быть получен разными способами и, в частности, способом разбивки на заданной территории геометрических фигур (сетки квадратов, треугольников) и способом послойного сложения объёмов, заключённых между плоскостями смежных горизонталей.

В первом случае поступают следующим образом. На карте в пределах заданной территории разбивают сетку квадратов (см. рис. 40).

Объём тела в пределах каждого квадрата будет равен объёму усечённой четырёхгранной призмы, и чем ближе верхнее основание к плоскости, тем точнее будет получен объём

V = S h_ср, (51)

где S – площадь квадрата, h_ср – среднее арифметическое из рабочих отметок четырёх вершин квадрата.

Здесьh_ср будет равно

h_ср =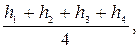

где h_i = H_i – Н _исх, Н_исх = Н_min на участке, Н_i – отметки вершин квадратов., определённых по горизонталям.

Рис. 40. Схема определения объёмов земляных масс

Общий объём тела в пределах контура АВСD будет равен

V = (52)

где S – площадь квадрата, h₁ – рабочая отметка для вершин, не являющихся общими для нескольких квадратов, h₂, h₃, h₄ – рабочие отметки для вершин, которые являются общими для двух, трёх и четырёх квадратов.

Если тело каждой четырёхгранной призмы разделить диагоналями на трехгранные призмы, например, по направлениям DВ или СА, то объём каждого из них определяется по той же формуле (52), но с учётом того, что S – площадь треугольного основания призмы, а h_ср – среднее арифметическое из рабочих отметок вершин треугольника

h_ср = .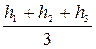

Общий объём тела в пределах контура АВСD будет равен

V = (53)

где индексы 1,2,3,6 – имеют те же значения, что и в формуле (52).

На рис. 40 показана схема определения объёма земляных масс для трёх вариантов: по квадратам, по треугольникам в направлении DB и в направлении СА. При заданной величине высоты сечения рельефа и масштаба карты объём тела в пределах контура АВСD имел три разных результата:

V³_DB < V⁴ < V³_CA

Причём в одном случае объём по квадратам был больше объёма по треугольникам на 2%, а в другом – меньше на 2%, то есть являлся средним арифметическим из объёмов по треугольникам

V⁴ = V_ср = .

Между собой объёмы по треугольникам отличаются на 4%.

Отсюда следует, определение объёмов земляных масс на карте с горизонталями в пределах замкнутого контура надёжнее производить при разбивке сетки квадратов. Точность полученного результата зависит от размеров квадратов и высоты сечения рельефа. Высота сечения рельефа влияет на точность положения горизонталей, то есть на точность определения отметок вершин квадратов. В целом можно принять погрешность определения отметок точек по горизонталям равной:

в равнинной местности – 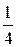h_c, в пересечённой местности – _с,

в горной местности – 1h_c.

Однако существуют и дополнительные требования с учётом масштаба, например, _с при съёмке в масштабах 1:5000 и 1:500 для местности с углами наклона до 2⁰ и _с при углах наклона от 2 до 6⁰.

При вертикальной планировке строительных площадок требования к точности определения объёмов выемок и насыпей резко возрастают. Поэтому разбивка сетки квадратов производится непосредственно на местности и отметки вершин квадратов определяются путём геометрического нивелирования. Это совсем другой класс точности. Для подсчётов земляных масс используются теже формулы, что и при решении поставленных выше задач на карте с горизонталями.

Во втором случае определение объёма тела в пределах контура АВСD путём послойного сложения объёмов тел, заключённых между плоскостями смежных горизонталей (см. рис. 40, слой выделен светло-серым цветом), сводится к определению для всех слоёв площадей верхней и нижней плоскостей усеченного конуса и умножению их полусуммы на высоту сечения рельефа

V = 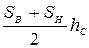(54)

Площадь верхнего и нижнего оснований усечённого конуса определяется в пределах каждой горизонтали или, в случае её не замыкания в пределах данного контура, в пределах горизонтали и границы контура, замыкающей концы этой горизонтали.

При определении объёмов водохранилищ поступают так же, как и при определении объёмов земляных масс, но с учётом специфики образования усечённых призм. В этом случае нижние основания призм будут совпадать с поверхностью водохранилища (с проектной отметкой затопления местности), а верхние с поверхностью его дна. Следовательно, рабочие отметки в вышеприведенных формулах будут равны разности проектной отметки и отметок вершин квадратов, полученных по горизонталям.

При определении объёма водохранилищ может быть целесообразно использовать способ послойного сложения объёмов воздушных слоёв, равных по высоте сечению рельефа, а по площади границей, образованной горизонталью и створом плотины АВ (рис.41).

А

Дата добавления: 2015-06-04