Дифракція Фраунгофера на дифракційній решітці

Розподіл інтенсивності. Дифракційна решітка утворюється періодичною повторюваністю прозорих (шириною b) та непрозорих плоскопаралельних ділянок (шириною а) на прозорій (наприклад, скляній) поверхні BCG (див.Мал.10). Величина

d = b + a (1)

називається періодом або сталою решітки. При освітленні решітки світлом, що падає нормально на її поверхню, в напрямку j відбувається інтерференція N 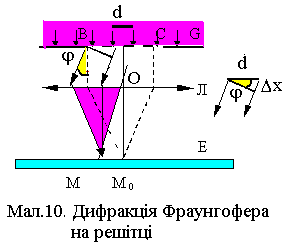променів світла від усіх щілин, із сталою величиною зсуву фаз

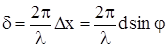, (2)

де Dх ¾ різниця ходу між променями сусідніх прозорих щілин.

Процес інтерференції світла від багатьох прозорих щілин можна описати за допомогою багатопроменевої інтерференції, розглянутої у §8.а). Результуюча амплітуда з урахуванням (2) може бути записати у вигляді

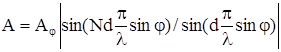(3)

де 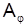¾ амплітуда хвилі, що утворюється дифракцією від окремої прозорої щілини в напрямку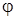

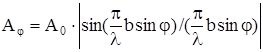. (4)

У цьому виразі А₀ ¾ амплітуда коливань у точці , при дифракції від однієї щілини у напрямку .

Максимуми виразу (3), що задаються умовою

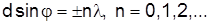. (5)

називаються головними. Амплітуда головного максимуму дорівнює

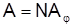. (6)

Величина n називається порядком головного максимуму. Головні мінімуми задаються умовою

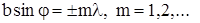(7)

Якщо з умови головного максимуму підставити

,

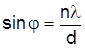у вираз (3), то амплітуда головного максимуму n-го порядку запишеться у вигляді

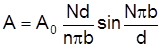. (8)

Головні максимуми розмежовані між собою мінімумами, які задаються умовою

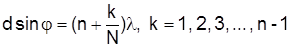. (9)

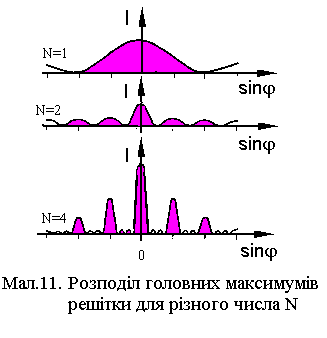
Таким чином між двома сусідніми головними максимумами знаходяться (N - 1) мінімум та (N - 2) додаткових максимуми.

На Мал.11 представлено розподіл головних максимумів при різних значеннях числа щілин N в решітці.

Дата добавления: 2015-06-04