
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производная по направлению. Градиент
|
|
|
|
Лекция № 6-7
Пусть функция 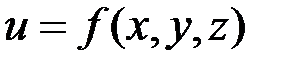 определена в некоторой окрестности точки
определена в некоторой окрестности точки 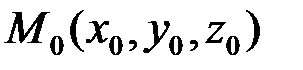 и дифференцируема в
и дифференцируема в 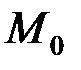 .
.
Рассмотрим всевозможные лучи, выходящие из  . Каждый луч задается единичным вектором
. Каждый луч задается единичным вектором  с координатами
с координатами  и определяет некоторое направление.
и определяет некоторое направление.
Фиксируем луч, выходящий из точки  . На прямой, содержащей этот луч, возьмем точку
. На прямой, содержащей этот луч, возьмем точку 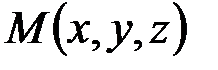 и рассмотрим вектор
и рассмотрим вектор  . Так как
. Так как 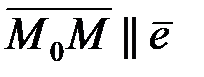 , то
, то 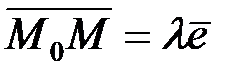 , или
, или
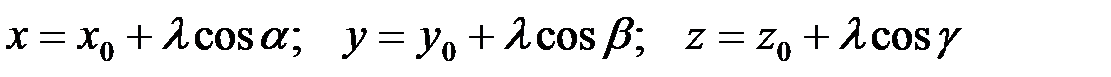 . (1)
. (1)
Равенство (1) показывает, что на прямой, проходящей через точку  и определяемой вектором
и определяемой вектором  , функция
, функция 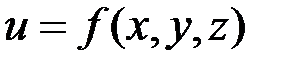 представляет собой сложную функцию одной переменной
представляет собой сложную функцию одной переменной 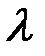 .
.
Определение. Производную указанной сложной функции по переменной 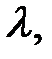 взятую в точке
взятую в точке  , называют производной функции
, называют производной функции 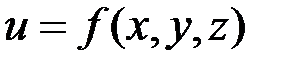 в точке
в точке  по направлению, определяемому единичным вектором
по направлению, определяемому единичным вектором  .
.
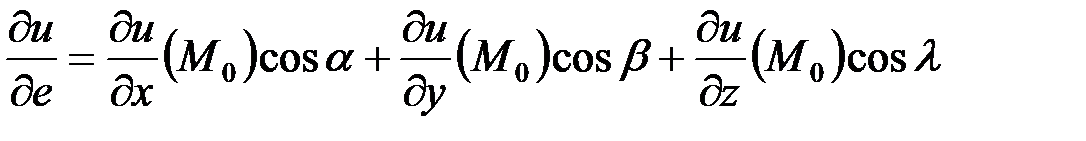 . (2)
. (2)
Определение. Градиентом функции 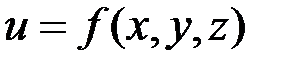 в данной точке
в данной точке  называется вектор, координаты которого имеют вид
называется вектор, координаты которого имеют вид 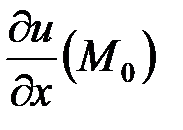 ,
, 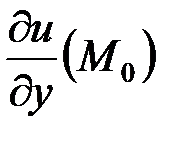 ,
, 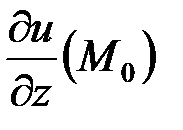 .
.
 . (3)
. (3)
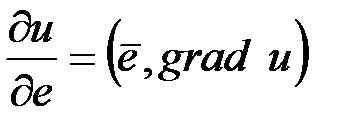 . (4)
. (4)
Производная функции 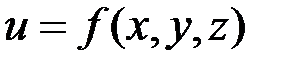 в точке
в точке  по направлению, определяемому градиентом этой функции, имеет максимальное значение по сравнению с производной в этой точке по любому другому направлению. Значение производной функции
по направлению, определяемому градиентом этой функции, имеет максимальное значение по сравнению с производной в этой точке по любому другому направлению. Значение производной функции 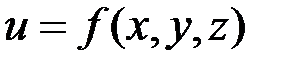 по направлению, определенному градиентом этой функции в данной точке равно
по направлению, определенному градиентом этой функции в данной точке равно 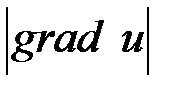 .
.
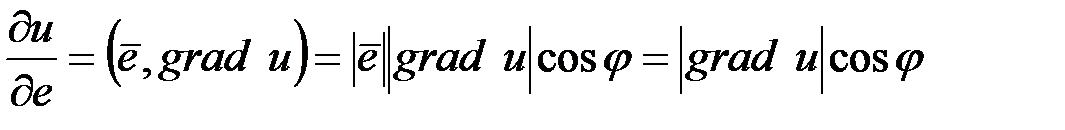 .
.
Таким образом, направление градиента – направление быстрейшего роста функции; противоположное направление – направление быстрейшего уменьшения функции. Направления, перпендикулярные к направлению градиента – направления постоянства функции.
Для функции 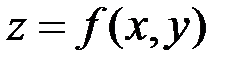 направление градиента перпендикулярно линиям уровня.
направление градиента перпендикулярно линиям уровня.
Для функции 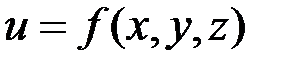 направление градиента перпендикулярно поверхностям уровня.
направление градиента перпендикулярно поверхностям уровня.
Если градиент функции находится не в фиксированной точке  , то этот вектор называется полем градиента функции
, то этот вектор называется полем градиента функции  .
.
Пример 1. Дана функция 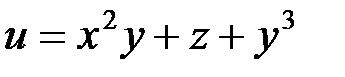 . Найти
. Найти 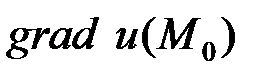 и
и 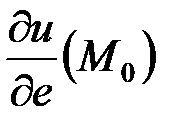 , где
, где  ;
; 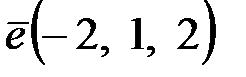 .
.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 555; Нарушение авторских прав?; Мы поможем в написании вашей работы!