Теория квантовых переходов. Типы квантовых переходов. Постановка задачи. Уравнения Шредингера для амплитуды вероятности перехода

Квантовые переходы скачкообразные переходы квантовой системы (атома, молекулы, атомного ядра, твёрдого тела) из одного состояния в другое. Наиболее важными являются К. п. между стационарными состояниями (См. Стационарное состояние), соответствующими различной энергии квантовой системы, — К. п. системы с одного уровня энергии (См. Уровни энергии) на другой. При переходе с более высокого уровня энергии Ek на более низкий Ei система отдаёт энергию Ek — Ei, при обратном переходе — получает её (рис.). К. п. могут быть излучательными и безызлучательными. При излучательных К. п. система испускает (переход Ek → Ei) или поглощает (переход Ei → Ek) квант электромагнитного излучения — Фотон — энергии hν (ν — частота излучения, h — Планка постоянная), удовлетворяющей фундаментальному соотношению

Ek - Ei = hν, (1)

(которое представляет собой закон сохранения энергии при таком переходе). В зависимости от разности энергий состояний системы, между которыми происходит К. п., испускаются или поглощаются фотоны радиоизлучения, инфракрасного, видимого, ультрафиолетового, рентгеновского излучения, γ-излучения. Совокупность излучательных К. п. с нижних уровней энергии на верхние образует спектр поглощения данной квантовой системы, совокупность обратных переходов — её спектр испускания (см. Спектры оптические).

Типы квантовых переходов: излучательные квантовые переходы, безызлучательные квантовые переходы.

При безызлучательных К. п. система получает или отдаёт энергию при взаимодействии с др. системами. Например, атомы или молекулы газа при столкновениях друг с другом или с электронами могут получать энергию (возбуждаться) или терять её.

Важнейшей характеристикой любого К. п. является вероятность перехода, определяющая, как часто происходит данный К. п. Вероятность перехода измеряют числом переходов данного типа в рассматриваемой квантовой системе за единицу времени (1 сек); поэтому она может принимать любые значения от 0 до ∞ (в отличие от вероятности единичного события, которая не может превышать 1). Вероятности переходов рассчитываются методами квантовой механики.

В классической физике механическое движение означает изменение координат частиц со временем. В квантовой механике движение означает изменение амплитуд вероятности со временем. Это означает, что амплитуды вероятности должны быть функциями времени: Y=Y(t). Простейшим законом изменения амплитуд со временем является закон изменения амплитуды вероятности в состоянии с определенной энергией или, говоря иначе, в стационарном состоянии. Как выше было получено –

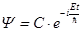. (15)

Проще не бывает.

При описании движения частицы в пространстве надо задать амплитуду вероятности в каждой точке. Например, частица совершает одномерное движение. В каждой точкеx должно быть определено значение амплитуды вероятности. Это означает, что Y=Y(x). Но, как выше было заявлено, должна быть еще зависимость от времени. Поэтому, как минимум, амплитуда вероятности должна быть функцией двух переменных: Y=Y(x, t).

Для примера, амплитуды вероятности, описывающие свободное движение не взаимодействующей ни с чем частицы выглядят так:

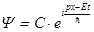. (16)

Вероятность застать частицу в точке x в момент времени t, в соответствии со смыслом амплитуды вероятности равна

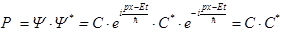. (17)

Как видно, вероятность не зависит ни от времени, ни от координат. Как масло равномерно размазана по всему пространству. Но вероятность не может быть больше 1, значит, по всему пространству равномерно размазана единица. Слой масла бесконечно тонкий.

В старые времена функцию, описывающую распределение амплитуд вероятности в любой момент времени, назвали волновой функцией, т.е. Y=Y(x, t) является волновой функцией частицы, совершающей одномерное движение.

Дата добавления: 2015-06-04