
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Базис мн вект. Коорд вект. Теор о корд вект
|
|
|
|
Признаки коллинеарности векторов
1. 2 вектора колинеарны тогда и только тогда когда их векторное производ = 0 вектору. 2. Вектора А и В наз. Калинеарными, если они лежат на одной прямой или на параллельных прямых. Калинеарными могут быть одинакова или противоположно направлены.нулевой вектор считается любому вектору.
12. Признаки компланарности векторов. 3 вектора комплонарны тогда и только тогда когда их смешенное производ = 0. Если среди 3 векторов хотя бы один нулевой или два любые колинеарны, то такие векторы комплонарны. 3 вектора в прост наз. комплонарными, если они лежат в одной плоскости или в параллельных плоскостях.
13.Теор о лин зав 4 вектар. 4 вектора всегда лин завис. Док. Если среди 4 вект. А,в,с,д есть 0; есть пара колин вект, либо 3 компл вект, то 4 вект явл лин завис. След исключаем все указан случаи и привед их векторы к общ началу. С=ОМ+МС ОМ=ОА+ОВ С=ОА+ОВ+МС ОАǁǁа ОА=£а ОВǁǁв ОВ=ßв МСǁǁд МС=ɤд С=£а+ßв+ɤд. ч.и.т.д.
Определение. Если 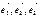 - базис в пространстве и
- базис в пространстве и  , то числа a, b и g - называются компонентами или координатами вектора
, то числа a, b и g - называются компонентами или координатами вектора  в этом базисе.В связи с этим можно записать следующие свойства:
в этом базисе.В связи с этим можно записать следующие свойства:
1)равные векторы имеют одинаковые координаты,
2)при умножении вектора на число его компоненты тоже умножаются на это число,
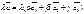 =
= 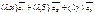 .
.
3)при сложении векторов складываются их соответствующие компоненты.
 ;
; 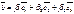 ;
;
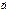 +
+ 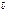 =
= 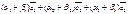 .
.
Теорема. Если А(x1,y1,z1),В(x2,y2,z2) то AB(x2-x1, y2-y1,z2-z1) другими сл чтобы найти корд вект нужно от корд конца отнять соотв корд начала. Док.
 Из усл след что ОА=(x1,y1,z1), а ОВ=(x2,y2,z2) очевидно что ОВ=ОА+АВ след АВ=ОВ-ОА след АВ= (x2,y2,z2)-(x1,y1,z1)= (x2-x1, y2-y1,z2-z1).
Из усл след что ОА=(x1,y1,z1), а ОВ=(x2,y2,z2) очевидно что ОВ=ОА+АВ след АВ=ОВ-ОА след АВ= (x2,y2,z2)-(x1,y1,z1)= (x2-x1, y2-y1,z2-z1).
15.Базис прямой,плоскости, простр. Опр. 1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.3) Базисом на прямой называется любой ненулевой вектор. См 14 вопрос.
16.Сист корд. Коорд точки. Система координат.
Понятие системы координат представляет собой совокупность точки начала отсчета (начала координат) и некоторого базиса Декартова система координат.
Зафиксируем в пространстве точку О и рассмотрим произвольную точку М.Вектор 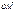 назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора. Опр. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.
назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора. Опр. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.
1-я ось – ось абсцисс 2-я ось – ось ординат 3-я ось – ось апликат
Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.
Если заданы точки А(x1, y1, z1), B(x2, y2, z2), то  = (x2 – x1, y2 – y1, z2 – z1).
= (x2 – x1, y2 – y1, z2 – z1).
Опр. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице. Опр. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат. Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х1, y1, z1), B(x2, y2, z2), то 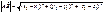 .
.
Если точка М(х, у, z) делит отрезок АВ/l, то координаты этой точки определяются как:
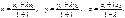
В частном случае координаты середины отрезка находятся как:x = (x1 + x2)/2; y = (y1 + y2)/2;
z = (z1 + z2)/2.
17.Выч корд вект АВ через корд т А и В. Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х1, y1, z1), B(x2, y2, z2), то 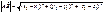 .
.
Если точка М(х, у, z) делит отрезок АВ/l, то координаты этой точки определяются как:
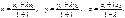
В частном случае координаты середины отрезка находятся как:x = (x1 + x2)/2; y = (y1 + y2)/2;
z = (z1 + z2)/2.
18.Задача о делении отрезка в данном отношении. Требуется разделить отрезок АВ, соединяющий точки А (х; у) и В(х2;у2) в заданном отношении Л > 0, т.е. найти координаты точки М(х;у) отрезка АВ такой, что AM/MB = Л. Решение: Введем в рассмотрение векторы АМ и МВ. Точка М делит отрезок АВ в отношении Л, если АМ = Л * МВ. Но АМ = {х – х1; у – у1), т. е. АМ = (х – х2)i+ (у – y1) j и МВ = (х2 – x; у2 - у), т. е. МВ = (х2 — х)i + (у2 - у) j - Уравнение принимеaт вид (х – х1)i + {у-у1)j = Л(x2 - х)i + Л (у2 - у)j. Учитывая, что равные векторы имеют равные координаты, получаем 1) x-x1=Лx2-Лx, 2)y-y1=Лy2-Лy. Формулы называются формулами деления отрезка в данном отношении. В частности, при Л = 1, т. е. если АМ = МВ, то они примут вид x=  , y=
, y= 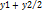 . В этом случае точка М (х; у) является серединой отрезка АВ.
. В этом случае точка М (х; у) является серединой отрезка АВ.
 19.Проекция вектора на ось. Формула выч проек. Прямая с задан полож напр наз осью. L
19.Проекция вектора на ось. Формула выч проек. Прямая с задан полож напр наз осью. L
Опр. Проек в А на ось l наз т пересеч оси l с перпенд ей плоск переход через т А. Опр. Проек АВ на ось l наз число равное ǁА’ǁǁB’ǁ взята полож, если вект А’B’ совпод с направл оси, и со знаком -, если напр А’B’ против с напр оси, где А’B’ – проекц т А и В соотв т.е проекц вект АВ на ось = l. Теорема. Проекц а на ось вычисл по форм прla=ǁaǁcosα, α-угол между а и осью. Док. АВ=а
прla=ǁА’B’ǁ=ǁАСǁ. Треуг АВС прямоуг. Угол С=90 АС-катет АВ-гипот.  ǁАСǁ=ǁ АВǁ
ǁАСǁ=ǁ АВǁ 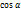 =ǁаǁ
=ǁаǁ 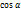 след прla=ǁАСǁ= ǁаǁ
след прla=ǁАСǁ= ǁаǁ 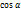 .
.
20.Теор о связи прямоуг корд вектора и проекц на корд оси. Следств. Теорема. В прямоуг декарт сист корд корд произв вект d=(x,y,z) = проекц этого вект на соотв корд оси т.е x=прOXd, y=прOYd, z=прOZd. Док. Очевидно OD=d=OM+MD OM=OA+OB MD=OC d=OA+OB+OC OAǁǁl зн OA=ƛi ǁOAǁ=ǁƛǁǁiǁ=ǁƛǁ=ƛ ƛ=ǁOAǁ OA=ƛi=ǁOAǁi ǁOAǁ=прOXd OA↑↓I то ƛ<0 ǁƛǁ=-ƛ ƛ=-ǁOAǁ OA=прOXdi анолог OB,OC след d=OA+OB+OC=прOXdi+прOYdj+прOZdr т.к корд вект наз коэф разлож вект по базису то d=(прOxd,прOYd,прOzd), т.к корд вект опред однозн в данном базисе то….
След1. ǁdǁ=(x,y,z)= 
След2. 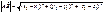 .
.
След3. Если αßɤ-углы обр d=(x,y,z) с соотв осями корд то cosα=  cosß=
cosß=  cosɤ=
cosɤ= 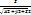
Cosα,cosß,cosɤ - наз направл cosd.
21.Линейн св-ва проекц. Теорема. Для любого А и В проекц их суммы = сумме проекц слагаем и проекц произв вект на число = числу умнож на проекц вект. Прl(a+b)=прla+прlb прlƛ(a)=ƛпрla Док. Возьмём прямоуг сист корд в котор OX совпод с Ol. Пусть a=(x1,y1,z1) b=(x2,y2,z2) корд вект = проекц его на корд оси т.е x1=прOXa=прla x2=прOX=прlb при слож вект их соотв корд склад a+b=(x1+x2,y1+y2,z1+z2) x1+x2=прla+прlb.
22.Коорд суммы вект и вектора ƛа. Или см 21 вопрос. Координаты вектора суммы двух векторов удовлетворяют соотношениям:
 и
и 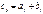 Вектор суммы двух векторов:
Вектор суммы двух векторов:
 Координаты вектора суммы нескольких векторов удовлетворяют соотношениям:
Координаты вектора суммы нескольких векторов удовлетворяют соотношениям:
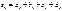
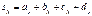 Сумма нескольких векторов:
Сумма нескольких векторов:
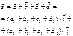
23.Формула для вычисл модуля вектора. Длина направленного отрезка, изображающего вектор, называется длиной, или модулем, вектора. Длина вектора  обозначается
обозначается 

24.Направляющ косинусы вект, их св-ва. Сумма кв напр cosd=1т.е cosквα+cosквß+cosквɤ=1. Если αßɤ-углы обр d=(x,y,z) с соотв осями корд то cosα=  cosß=
cosß=  cosɤ=
cosɤ= 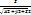
Cosα,cosß,cosɤ - наз направл cosd.см 21 вопр.
25. Скалярн произв вект. Его св-ва. Вычисл в корд. Опр. Скалярным произведением векторов 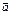 и
и 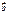 называется число, равное произведению длин этих сторон на косинус угла между ними.
называется число, равное произведению длин этих сторон на косинус угла между ними.
 ×
×  = ï
= ï 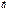 ïï
ïï 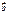 ïcosj
ïcosj
Свойства скалярного произведения:
1) 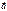 ×
× 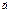 = ï
= ï  ï2;
ï2;
2) 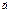 ×
×  = 0, если
= 0, если 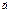 ^
^ 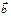 или
или 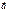 = 0 или
= 0 или 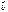 = 0.
= 0.
3) 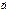 ×
× 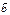 =
= 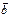 ×
× 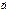 ;
;
4) 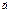 ×(
×(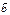 +
+  ) =
) = 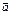 ×
× 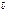 +
+ 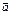 ×
×  ;
;
5) (m 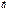 )×
)× 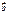 =
=  ×(m
×(m 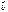 ) = m(
) = m(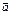 ×
× 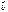 );
);
Если рассматривать векторы  в декартовой прямоугольной системе координат, то
в декартовой прямоугольной системе координат, то 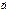 ×
× 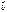 = xa xb + ya yb + za zb; Используя полученные равенства, получаем формулу для вычисления угла между векторами:
= xa xb + ya yb + za zb; Используя полученные равенства, получаем формулу для вычисления угла между векторами:
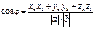 ;
;
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 449; Нарушение авторских прав?; Мы поможем в написании вашей работы!