Сист лин уравн. Осн понятия

Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом: ,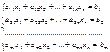

где a_ij – коэффициенты, а b_i – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество. Опр. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной. Опр. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного. Опр. Для системы линейных уравнений вида матрицаА = называется матрицей системы, а матрицаА называется расширенной матрицей системы

Опр. Если b₁, b₂, …,b_m = 0, то система называется однородной. однородная система всегда совместна.

49. Теор Крамера. Теорема. Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

x_i = D_i/D, где D = det A, а D_i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i.D_i =

50. Метод Гаусса. В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в послед исключении неизвестных.

Рассмотрим систему линейных уравнений: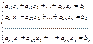

Разделим обе части 1–го уравнения на a₁₁ ¹ 0, затем:1) умножим на а₂₁ и вычтем из второго уравнения2) умножим на а₃₁ и вычтем из третьего уравнении. Получим:

, где d_1j = a_1j/a₁₁, j = 2, 3, …, n+1.

d_ij = a_ij – a_i1d_1j i = 2, 3, …, n; j = 2, 3, …, n+1. Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.

51.Теор Крон-Капелли. Следствия.Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA^*.

Очевидно, что система может быть записана в виде:

x₁ + x₂ + … +x3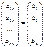

Док. 1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А^* не изменяют ранга.2) Если RgA = RgA^*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше. след1. Если ранги основн и расш м равны числу r, то Mr уравн каэф котор необход в базисн минор можно вычеркн из системы. След2. Если ранги осн и расш м совпод с числ неизв n то системы имеют един реш. RgA = RgA^*=n. След3. Если ранги осн и расш м равны и явл числом < числа неизв то сист имеет беск мн реш.

52. Исследование системы линейных уравнений.Необходимость. Так как ранг не может превосходить размера матрицы, то, очевид­но, г ^ п. Пусть г = п. Тогда один из миноров размера п х п отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение: Х{ = — О, Л,- = О, Д ф 0. Значит, других, кро­ме тривиальных, решений нет. Итак, если есть нетривиальное решение, то г < п. Достаточность. Пусть г < п. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т. е. имеет и ненулевые решения

53.Ситс однородн лин уравн. Теор о сущ ненулев решен. Система однородных уравнений всегда имеет нулевое решение. Если ранг матрицы меньше числа неизвестных, то система имеет бесчисленное множество решений. Для того, чтобы система имела ненулевые решения, необходимо, чтобы ее определитель был равен нулю. Теорема. Сист одн мн ур имеет не нулев решен т.и.т.т.к ранг её осн м меньше числа неизв. Следс1. Кв однор лин сист имеет не нулев решен т.и.т.т.к опр её осн=0. Св-ва: 1) опер слаж. 2) умн.

54. Фундам сист решен. Теор фунд сист реш. Фунд сист решен одн лин сист наз базис прост всех её решен.Если: 1) лин незав. 2)лин наиб решен. Теорема. Если ранг осн м одн лин сист =r а число неизв =n то сист имеет фунд сист реш сост из n-r реш. Док. Расм случай когда Rg A=r=n в этом сл сист имеет един нул реш обр нул простр. Нулев простр не имеет базиса т.к нул вект всегда лин завис т.е фунд реш сист сост из n-r=n-n=0.

56.Прост св-ва лин простр.Св-ва:

1)сущ ед нуль эл.

2)ед противоп эл.

3)0*x=0. 4)α*0=0. 5)-x=(-1)x.

6)-(αx)=(-α)x=α(-x) 7)(α-ß)x=αx-ßx.

57. Примеры линейных пространств. V - множество сост. Из всех диствительных чисел. Нетрудно проверить что для него выполняется все оксеомы лин пространства и поэтому оно является линейным пространство, поэтому действительные числа одновременно являются векторами лин. пространства.

58. Линейная зависимость множества векторов линейного пространства. 1. Вектор х=А₁х₁+А₂х₂+..+А_nx_n где А1,А2,Аn –числа из поля Р, то говорят что вектор Х линейно выражается через векторы х1,х2,хn. 2. векторы х1,х2,xn.-линейно зависимыми если поле Р найдется число А1,А2,Аn одновременно не равны 0 для которых справедливо равенство А1Х1+А2Х2+АnХn=0.

59. Признаки линейной зависимости векторов в линейном пространстве. Теорема1: векторы х1,х2,xn€V являются линейным зависимым тогда и только тогда когда хотя бы 1 из них лин. выражен через остальные. 2. Если среди векторов х1,х1,хn, есть 0вектор, то все эти вектора линейно зависима. 3. Если среди векторов х1,х1,хn, есть подмножество лин. зависимых векторов, то и все вектора будут линейно зависимыми.

Дата добавления: 2015-06-04