
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Угол между векторами
|
|
|
|
Определения угла ᵠ между нулевыми векторами a=(ax; ae; az) b=(bx;by;bz)
CosV= 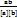 т.е. cosV=
т.е. cosV= 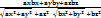
Отсюда следует пенпердикулярность векторов а и b.а┴в 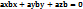
27.Услов ортог двух вект. 2 вект ортоган т.и.т.т когда их скалярн произв =0. Док. 1неох. а┴b α=(a,b)=90 cos90=0 ab=ǁaǁǁbǁcos90=0 2дост. Ab=0 если 1 из вект 0 то a и b –ортог, поэт пусть a и b не нулев. ǁaǁ≠0≠ǁbǁ тогда ǁaǁǁbǁcosα=0 зн cosα=0 α=90 зн a┴b.
28.Правые и лев тройки вект. Пусть задана тройка (a,b,c) некомпл вект. Отложим эти вект от некот т О, т.е построим соотв направл отрезки ОА,ОВ, ОС. Если кратч поворот вокруг т О от отрезка ОА к отр ОВ, наблюд из т С, соверш против час стр, то тройка наз правой. В против случае эта тройка – левая.
29.Векторн произв двух вект. Его св-ва. Опр. Векторным произведением векторов 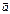 и
и 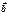 называется вектор
называется вектор 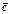 , удовлетворяющий следующим условиям:1)
, удовлетворяющий следующим условиям:1) 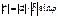 , где j - угол между векторами
, где j - угол между векторами 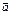 и
и 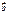 ,
,
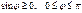 2) вектор
2) вектор 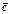 ортогонален векторам
ортогонален векторам 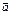 и
и 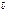 3)
3) 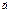 ,
, 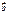 и
и 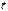 образуют правую тройку векторов.
образуют правую тройку векторов.
Обозначается: 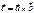 или
или 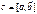 .
.
Свойства векторного произведения векторов:
1)  ;
;
2) 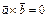 , если
, если 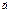 ïï
ïï 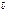 или
или 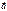 = 0 или
= 0 или 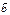 = 0;
= 0;
3) (m 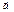 )´
)´ 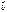 =
= 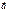 ´(m
´(m 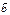 ) = m(
) = m(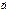 ´
´ 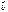 );
);
4) 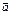 ´(
´(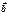 +
+ 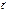 ) =
) = 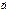 ´
´  +
+ 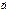 ´
´ 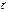 ;
;
5) Если заданы векторы 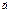 (xa, ya, za) и
(xa, ya, za) и 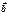 (xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами
(xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами 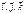 , то
, то
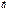 ´
´ 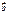 =
= 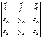
6.Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах 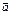 и
и 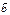 .
.
30. Вычисл прощ параллел и треуг. S параллел постр на a и b привед к общ началу = ǁa  bǁ.
bǁ.
S=ǁaǁǁbǁsinα=ǁa  bǁ Следств. S постр на a и b привед к общ началу = половине модуля их вект произв. S=
bǁ Следств. S постр на a и b привед к общ началу = половине модуля их вект произв. S=  ǁa
ǁa  bǁ.
bǁ.
31.Усл коллин двух вект. 2 вект коллин т.и.т.т.к их вект произв =0.
aǁǁb a  b=0 Док. 1необ. aǁǁb после привед коллин вект к общ началу они лежат на одной прямой. При этом возможно 2 сл:1)a↑↑b 2)a↑↓b
b=0 Док. 1необ. aǁǁb после привед коллин вект к общ началу они лежат на одной прямой. При этом возможно 2 сл:1)a↑↑b 2)a↑↓b
Соотв α=0 или α=180 sin0=sin180=0 ǁa  bǁ=ǁaǁǁbǁsinα=0 a
bǁ=ǁaǁǁbǁsinα=0 a  b=0 2дост.
b=0 2дост.
a  b=0 если один из них 0 то aǁǁb по опр. ǁaǁ≠0≠ǁbǁ т.к ǁa
b=0 если один из них 0 то aǁǁb по опр. ǁaǁ≠0≠ǁbǁ т.к ǁa  bǁ=ǁaǁǁbǁsinα=0 то сущ ед возм что sinα=0 α=0 или α=180 но в этом сл aǁǁb.
bǁ=ǁaǁǁbǁsinα=0 то сущ ед возм что sinα=0 α=0 или α=180 но в этом сл aǁǁb.
32.Выч векторн произв в корд. Если a(x1,y1,z1) b(x2,y2,z2) то a  b = через опр 3-го порядка формула.
b = через опр 3-го порядка формула.
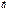 ´
´ 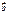 =
= 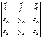
33.Смеш произв трёх вект. Опр. Смеш произв вект 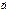 ,
, 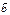 и
и 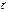 наз число, равное скалярному произв вект
наз число, равное скалярному произв вект 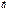 на вектор, равный векторному произв векторов
на вектор, равный векторному произв векторов  и
и  .Обозн
.Обозн 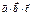 или (
или (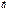 ,
, 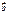 ,
,  ).
).
Смеш произв 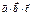 по модулю равно объему параллелепипеда, построенного на векторах
по модулю равно объему параллелепипеда, построенного на векторах 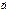 ,
, 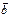 и
и 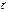 .
.
Свойствасмешанного произведения:
1)Смешанное произведение равно нулю, если:
а)хоть один из векторов равен нулю;
б)два из векторов коллинеарны;
в)векторы компланарны.
2) 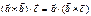
3) 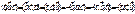
4) 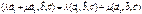
5) Объем треугольной пирамиды, образованной векторами 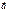 ,
, 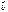 и
и 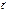 , равен
, равен 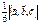
6)Если 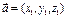 ,
, 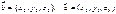 , то
, то
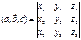
34.Призн компл трёх вект. 3 вектора комплан т.и.т.т.к их смешан произв =0.
35.Выч объёма параллел и тетраэдра. V тетр abc привед к общ началу =Vтетр=  ǁabcǁ.
ǁabcǁ.
Смешан произв abc= Vпараллелеп постр на abc прив к общ началу взятому со зн + если abc явл правой и со зн – если abc явл левой. Док.
Abc=(a  b)c=dc, где d=a
b)c=dc, где d=a  b ǁnǁ=1 d↑↑n зн d=ƛn ǁdǁ=ǁƛǁǁnǁ=ƛ=ǁa
b ǁnǁ=1 d↑↑n зн d=ƛn ǁdǁ=ǁƛǁǁnǁ=ƛ=ǁa  bǁ=S ƛ=S d=Sn abc=dc=Snc=Sǁnǁǁcǁcosα=Sǁcǁ* *cosα=SпрNc=Sh=V.
bǁ=S ƛ=S d=Sn abc=dc=Snc=Sǁnǁǁcǁcosα=Sǁcǁ* *cosα=SпрNc=Sh=V.
доSh) прNс=-ǁOMǁ=-h abc=SпрNc= S(-h)=-V. След1. V паралл постр на вект abc прив к общ началу = модулю смешан произв V=ǁabcǁ. След2. Смеш произ abc полож т.и.т.т.к 3 вект явл прав и соотв отриц – лев.
36.Выч смеш произв в корд. Если a(x1,y1,z1) b(x2,y2,z2) c(x3,y3,z3) то их смеш произв = опр 3-го порядка сост из соотв корд данных вект.
Abc= 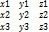
38. Понятие матрицы. Виды матрицы. Опр. Матрицей размера m´n, где m- число строк, n- число столбцов, наз табл чисел, расположенных в опр порядке. Эти числа наз эл матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересеч которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А = 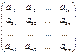
Опр. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.
Опр. Матрица вида:
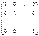 = E,
= E,
называется единичной матрицей.
Опр. Если amn = anm, то матрица называется симметрической.
Опр. Квадратная матрица вида 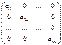 называется диагональной матрицей.
называется диагональной матрицей.
39.Слож матриц и умн на число. Опр. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.cij = aij ± bij Св-ва. 1)комут. 2)ассоц. 3)А+0=А 4)А+(-А)=0. Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.
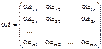
Св-ва. 1*А=А 2)….
40. Свойства линейных операций. 1. а + b = b+ а,
2. (а + b) + с = а + (b + с),
3. А1 • (А2 ■ а) = A1 ■ A2 ■ а,
4. (А1 + А2) • а = А1 • а + А2 • а,
5. А • (а + b) = А ■ а + А • b.
41.Произв матр. Св-ва произв. Опр: Произв матриц наз матрица, элементы которой могут быть вычислены по следующим формулам:
A×B = C;
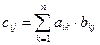 .
.
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Св-ва. 1) не коммутативно, т.е.
АВ ¹ ВА
2) ассоциативна, (АВ)С=А(ВС).
3) дистрибутивна
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
4) кв матрицыА×Е = Е×А =А
42. Понятие опр кв матрицы. Опр. Определителем квадратной матрицы А= 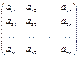 наз число, которое может быть вычислено по элементам матрицы по формуле: det A =
наз число, которое может быть вычислено по элементам матрицы по формуле: det A =  , где
, где
М1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов. Для указанной матрицы А число М1к наз дополн минором элемента матрицы a1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах. Опр. Дополнительный минор произвольного элемента квадратной матрицы aij равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.
43.Св-ва опридел. Св-во1. Важным свойством определителей является следующее соотношение: det A = det AT; 2. det (A ± B) = det A ± det B.
3. det (AB) = detA×detB
4. Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.
5. При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.
6. Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.
7. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)
8. Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.
44.Обратн матр. Теорема о сущ обр матр. Опр. Если существуют квадратные матрицы Х и А, удовлетворяющие условию: XA = AX = E,
где Е - единичная матрица того же самого порядка, то матрица Х называется обратной к матрице А и обозначается А-1.. св-ва. 1)ǁAA-1ǁ=ǁAǁǁA-1ǁ=ǁEǁ 2) (AB)-1 = B-1A-1 3) (AT)-1 = (A-1)T.
Теорема. Для того чтобы кВ м А имела обр необх и дост чтобы опред этой м был отличен от нуля, при этом обр м опред след выраж.
А-1= 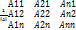 Док.
Док.
Для А сущ обр А-1 такая что А*А-1=Е использ св-ва 2. Очевидно что
ǁЕǁ=  =1 ǁАǁǁА-1ǁ=1 т.к произв 2 чисел =1. То ни один со мн≠0 т.е ǁАǁ≠0 ǁА-1ǁ≠0 т.е если м имеет обр то её опред всегда отлич от 0.
=1 ǁАǁǁА-1ǁ=1 т.к произв 2 чисел =1. То ни один со мн≠0 т.е ǁАǁ≠0 ǁА-1ǁ≠0 т.е если м имеет обр то её опред всегда отлич от 0.
45.Ранг матрицы. Опр. В матрице порядка m´n минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n. Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными. В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок. Опр. Порядок базисного минора матрицы называется рангом матрицы и обозначается Rg А.Очень важным свойством элементарных преобразований матриц является то, что они не изменяют ранг матрицы. Опр. Матрицы, полученные в результате элементарного преобр, называются эквивалентными. Надо отметить, что равные матрицы и эвивалентные матрицы - понятия совершенно различные.
46.Методы нахожд ранга матр. 1) Перестановка местами 2 параллельных рядов матрицы.
2)Умножение элементов ряда матрицы на число отличное от нуля, отличное от нуля.
3)Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.
47.Теор о базисн миноре. Её следствия.Теорема. В произвольной матрице А каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.Т.о, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице. Док. След1. Ранг м А= макс числу лин незав строк этой матр. След2. Опред кВ м А=0 т.и.т.т.к строки лин зав.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 436; Нарушение авторских прав?; Мы поможем в написании вашей работы!