Энтр-я и вер-ть. Т. Боль-на-Планка

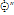Энтропия – функция состояния, то есть любому состоянию можно сопоставить вполне определенное значение энергии. Для одной молекулы вероятность равна , а для N молекул – . Общая вероятность – общий результат произведения вероятностей на каждый элемент. Равновесному состоянию соответствует максимальная вероятность. Следовательно, вероятность данного состояния является критерием, который определяет направление процесса и позволяет найти равновесие. В статистической термодинамике используется термодинамическая вероятность ω — число способов, которыми может быть реализовано состояние физической системы. Термодинамическая вероятность является числом математической вероятности и всегда много больше 1. ω – является функцией состояния и максимальна при равновесии. Пусть 2 системы в термодинамическом равновесии с ω₁ и ω₂ образуют сложную систему. ω₁₊₂= ω₁ ω₂. (1) Это свойство мультипликативность делает эту функцию неудобную для непосредственных расчетов, так как она не аддитативна. Она не связана с термодинамическими характеристиками системы и следовательно, найти такую функцию вероятности которая была бы связана с тепловыми характеристиками и обладало бы аддитативностью. Введем новую функцию 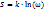(*) Так как система состоит из 2 частей, то (2) Графически положение молекул можно изобразить в виде точек так называемом в фазовом пространстве, осями которой выделяются все координаты и импульсы. При этом каждая опишется отображающей точкой в фазовом пространстве. Для полного механического описания моля одноатомного газа необходимо 6N чисел. Нет необходимости точно задавать число атомов, можно задавать с некоторой точностью координаты и импульсы ∆x, ∆y, ∆z, ∆P_x, ∆P_y, ∆P_z. Это точность зависит от характера задачи. Распределение должно описать, сколько находится в разных областях фазового пространства. Можно разделить фазовое пространство на области с одинаковыми объемами. Распределение опишется совокупностью N_i указывающих число молекул в каждой области. Так как каждому способу осуществления распределения молекулы в одной области отвечает все способы распределения в других областях, то общее число способов и размещения молекул в каждой области равно 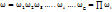где g – число ячеек. Для того чтобы найти равновесное распределение следует искать максимальную термодинамическую вероятность при учете что число молекул постоянно и общая энергия системы равна 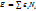где i – номер ячейки, а 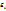- энергия молекулы в -той области. Вместо ω_max можно искать S_max. 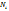Необходимо найти значение отвечающему максимуму величины S. 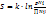. Имеются дополнительные условия постоянства частиц и энергии. Воспользуемся формулой Стирлинга: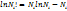 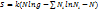(3) Воспользуемся неопределенным множителем Лагранжа. 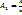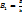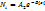Продифференцируем, приравняем нулю и решим и получится 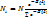(4) так как B₁=1/kT, то (5) – это уравнение Больцмана.

22. Распред-е мол-л по импульсам.

Рассмотрим распределение газа по составляющей импульса p_x.

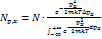(1)

Введем понятие плотности распр-я молекул (число молекул на единицу интервала):

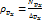(2)

Возьмем интеграл Пуассона:

(3)

получим

(4)

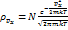(5)

Для рассмотрения рапр-я по импульсам определим число молекул

(6)

Для определения N_p надо просуммировать N_pxpypz по всем p_xp_yp_z,относящиеся к данному значению p:

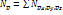
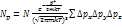(7)

Сумма выражает объем импульсного пространства, отвечающего изменению p на ∆p.

Этот объем равен 4πp2∆ p. Т.о:

(8)

Как видно из ур-я (8), вероятность иметь импульс p (в интервале ∆ p) опред-ся двумя факторами. Наряду с множителем e ^{- p 2/2 mkT} фигурирует геометр. вер-ть, передаваемая выражением 4πp². Большему значению р отвечает больший объем в импульсном пространстве. Малые значения р мало вероятны, так как им отвечает малая геометрическая вероятность.

Из ур-ния (8) легко рассчитать ср. вел-ну импульса:

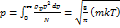(9)

Также получим:

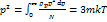(10)

Дата добавления: 2015-06-04