
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Практическое значение и методы определения показателей процесса восстановления
|
|
|
|
Если известно значение ω(x) для определенного интервала наработки, то для этого интервала можно оценить программу работ по устранению отказов N (x), потребность в запасных частях и материалах.
При оценке надежности изделия число отказов обычно относят к пробегу, а при оценке потока отказов, поступающих для устранения, – ко времени работы соответствующих производственных подразделений
| N (x) ≈L Σ(x) ω(x), | (3.6) |
где L Σ(x)— суммарная наработка группы автомобилей за период, для которого рассчитывается программа.
Например, за 15 рабочих дней группа автомобилей имела суммарную наработку L Σ=340 тыс. км. Согласно имеющимся данным, например, параметр потока отказов подвески ω=0,06 отказов/1000 км.
Суммарное количество требований на ремонт подвески за 15 рабочих дней составит N≈ 340 0,06=20,4 или, в среднем, 1,4 требования в смену.
Необходимо учитывать, что эти расчеты возможны для стадии стабилизации ω(x), т.е. начиная с наработки х >(1,2—1,4) 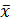 1 для первого и второго случаев (см. рисунок 3.6).
1 для первого и второго случаев (см. рисунок 3.6).
Следует отметить, что ведущая функция и параметр потока отказов определяются аналитически лишь для некоторых видов законов распределения. Например, для экспоненциального закона
Ω(X)= X ω= X /η 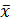 1,
1,
откуда ω=1/η 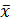 1=const.
1=const.
При η=1 ω=1/ 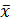 =const.
=const.
Для нормального закона
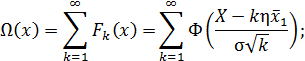
| (3.7) |

| (3.8) |
где Ф — нормированная функция для z =(X - k η 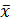 1)/(σ√ k);
1)/(σ√ k);
k — порядковый номер отказов (в том числе замен).
Пример. Наработка до первой замены накладок сцепления 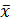 =58 тыс. км, среднее квадратическое отклонение σ=10 тыс. км, коэффициент восстановления ресурса η = 0,6. Определить возможное число замен при наработке автомобиля 150 тыс. км. Для расчетов используем формулу (3.7), последовательно определяя F 1(150)=Ф(150-1 58)/10=Ф(9,2)=1 (см приложение Б); F 2(150)=Ф(150-2 0,6 58)/(10 21/2)=Ф(5,7)=1; далее F 3(150)=0,995; F 4(150)=0,69; F 5(150)=0,136; F 6(150)=0,007.
=58 тыс. км, среднее квадратическое отклонение σ=10 тыс. км, коэффициент восстановления ресурса η = 0,6. Определить возможное число замен при наработке автомобиля 150 тыс. км. Для расчетов используем формулу (3.7), последовательно определяя F 1(150)=Ф(150-1 58)/10=Ф(9,2)=1 (см приложение Б); F 2(150)=Ф(150-2 0,6 58)/(10 21/2)=Ф(5,7)=1; далее F 3(150)=0,995; F 4(150)=0,69; F 5(150)=0,136; F 6(150)=0,007.
Ввиду того что F 6мало, последующие расчеты для F 7 и других можно не производить. Таким образом, к пробегу 150 тыс. км возможное накопленное число замен данной детали на один автомобиль
Ω(150)= Σ6 k =1Ф(z)=1+1+0,995+0,69+0,136+0,07≈3,83.
Для практического использования важны некоторые приближенные оценки ведущей функции параметра потока отказов
| F (X)≤Ω(X)≤ F (X)/(1- F (X)). | (3.9) |
Из этой формулы следует, что на начальном участке работы, где преобладают первые отказы, т.е. F (X)≤1, Ω(X)≈ F (X).
Ведущая функция параметра потока отказов стареющих элементов для любой наработки удовлетворяет следующему неравенству:
X/ (η 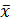 1) - 1≤Ω(X)≤ X/ (η 1) - 1≤Ω(X)≤ X/ (η 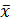 1). 1).
| (3.10) |
Для рассмотренного выше примера с заменой накладок сцепления, используя формулу (3.10), получим следующую оценку ведущей функции параметра потока отказов при наработке автомобиля X =150 тыс. км: 3,3≤Ω(x)≤4,3. Таким образом, к пробегу X в среднем (формула (3.10)) возможны от 3,3 до 4,3 отказов сцепления, по точным расчетам (формула (3.7)) – 3,83.
Для любого закона распределения наработки на отказ, имеющего конечную дисперсию D =σ2, ведущая функция параметра потока отказов при достаточно большом значении X определяется по следующей приближенной формуле:

| (3.11) |
При расчете гарантированных запасов необходима интервальная оценка ведущей функции параметра потока отказов (для достаточно больших значений X):
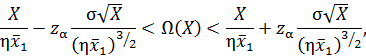
| (3.12) |
где za — нормированное отклонение для нормального закона распределения при условии, что число отказов (замен) с вероятностью 1-α будет заключено в данных пределах.
Пример. Определить для условий предыдущего примера ( =58 тыс. км; η=0,6; σ=10 тыс. км.) с достоверностью 1-α=0,9 необходимое число комплектов накладок сцепления за пробег автомобиля 150 тыс. км. Так как условия задачи требуют обеспечения накладками с вероятностью 90 %, то необходимо определить верхнюю границу потребности в накладках за 150 тыс. км пробега. Прежде всего определим нормированное отклонение при 1-α=0,9=Ф(z). Из приложения 5 имеем za= 1,25. Верхняя граница потребности в деталях составит Ω(150)=5,04. Следовательно, с вероятностью 90 % можно полагать, что за 150 тыс. км пробега потребуется не более пяти комплектов накладок сцепления. Средний же расход составит около 3,8 комплектов на один автомобиль.
=58 тыс. км; η=0,6; σ=10 тыс. км.) с достоверностью 1-α=0,9 необходимое число комплектов накладок сцепления за пробег автомобиля 150 тыс. км. Так как условия задачи требуют обеспечения накладками с вероятностью 90 %, то необходимо определить верхнюю границу потребности в накладках за 150 тыс. км пробега. Прежде всего определим нормированное отклонение при 1-α=0,9=Ф(z). Из приложения 5 имеем za= 1,25. Верхняя граница потребности в деталях составит Ω(150)=5,04. Следовательно, с вероятностью 90 % можно полагать, что за 150 тыс. км пробега потребуется не более пяти комплектов накладок сцепления. Средний же расход составит около 3,8 комплектов на один автомобиль.
Таким образом, используя значения параметра потока отказов, можно не только определить программу работ, но и оценить конкретный расход материалов и деталей за любой заданный период и планировать работу системы снабжения.
Параметр потока отказов может быть оценен также на основании экспериментальных данных (отчетных материалов, специальных наблюдений) следующим образом (см. рисунок 4.2):

| (3.13) |
где т (Δ x)— суммарное число отказов п автомобилей в интервале наработки от Х 1до Х 2(или времени работы от t 1 до t 2);
Ω(X 1) и Ω(X 2) – ведущие функции потока отказов к наработке X 1 и X 2.
При этом следует иметь в виду, что из-за неравномерности эксплуатации отдельных автомобилей (среднесуточный, месячный, годовой пробег) одинаковые наработки у отдельных автомобилей образуются в разные календарные интервалы времени. В результате конфигурации параметров потока отказов и потока требований на устранение этих отказов могут различаться.
Таким образом, потоки наработок на отказы изделий имеют следующие особенности, которые необходимо учитывать при организации ТО и ремонта автомобилей:
— отказы случайны у каждого автомобиля;
— независимы у разных автомобилей;
— происходит смешение отказов нескольких поколений;
— происходит смешение отказов у разных автомобилей;
— при устранении отказов в зоне ремонта безразлично, у какого автомобиля и какой по номеру отказ устраняется;
— значимы состав, трудоемкость и стоимость выполняемой работы;
— в определенных условиях может происходить относительная стабилизация потока отказов и требований, облегчающая организацию технологических процессов ТО и ремонта; важно знать эти условия и уметь аналитически рассчитывать показатели работы системы в этих условиях.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 835; Нарушение авторских прав?; Мы поможем в написании вашей работы!