
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обоснование параметров направляющей кривой
|
|
|
|
Как уже было отмечено, цилиндроидальная поверхность образована перемещением линейной образующей по направляющей кривой.
В качестве направляющей кривой обычно используют параболу, построенную на основе дуги окружности. Парабола представляет собой кривую с переменным радиусом кривизны, что способствует крошению почвы. Поскольку основной направляющей кривой является дуга окружности, то определяющим параметром ее становится радиус. От величины радиуса зависят размеры поверхности, причем они должны оказаться достаточными для размещения на ней почвенного пласта (рис.1.17).
Когда пласт, подрезанный лезвием лемеха АВ, деформируется и поместится на отвале, то линия СВ, перпендикулярная к лезвию должна быть размещена на поверхности в виде кривой 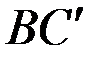 , т.е. длина дуги
, т.е. длина дуги 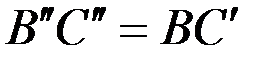 должна равняться прямой ВС.
должна равняться прямой ВС.
Так как
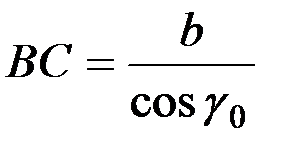 ,
,
а длина дуги
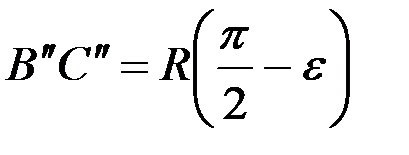
 ,
,
то
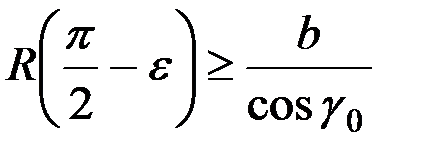 , (1.7)
, (1.7)
или
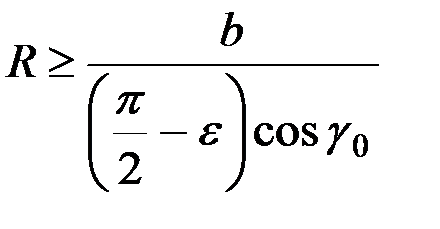 .
.
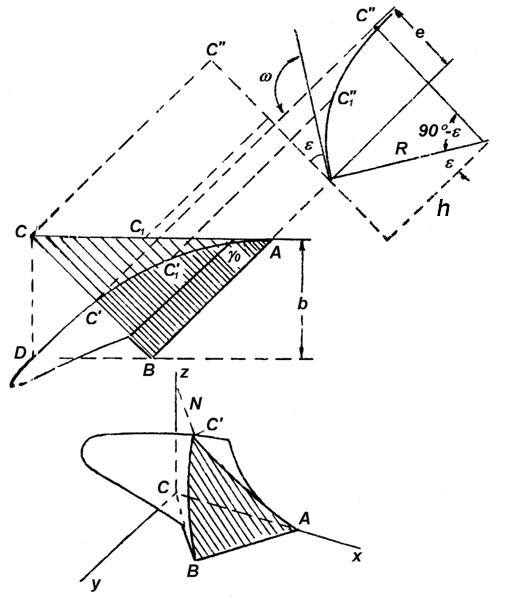
| Рис. 1.17. Размещение пласта на лемешно-отвальной поверхности |
Если радиус направляющей кривой взять меньше этого, то пласт не разместится на поверхности и почва будет пересыпаться через отвал, т.е. это наименьшее из возможных значений радиуса:
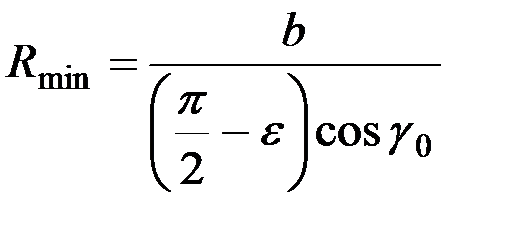 . (1.8)
. (1.8)
Верхний предел радиуса предложено определять, исходя из условия отсутствия задираемости пласта крылом отвала [1]. Это будет выполнено тогда, когда двугранный угол i между касательной к крылу плоскостью и поверхностью отваленного пласта будет меньше 90°, т.е. i < 90° (рис. 1.18).
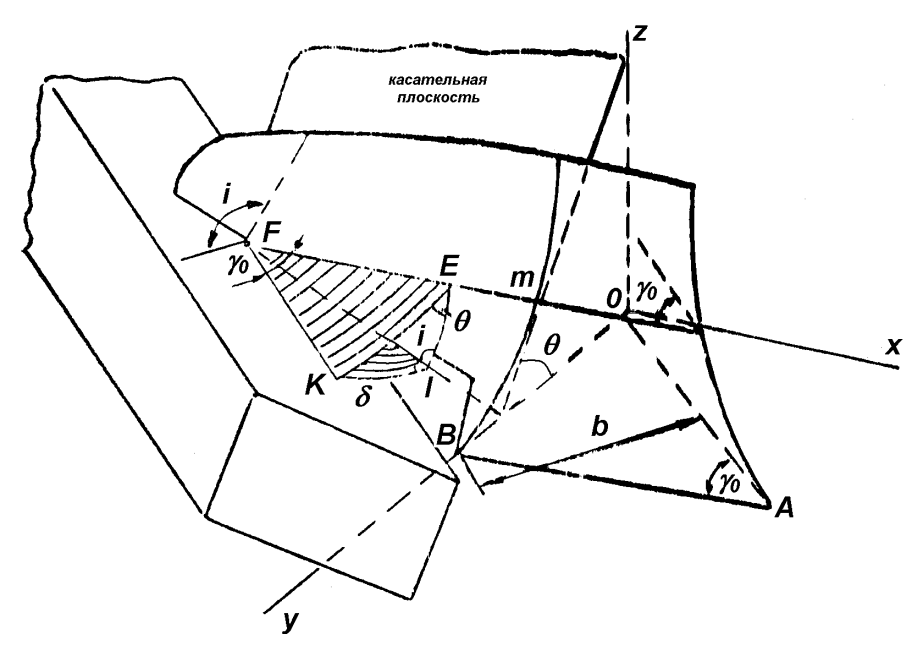
| Рис. 1.18. Взаимодействие крыла корпуса с верхней гранью отвального пласта |
Корпус плуга относительно осей координат размещен так, что лезвие лемеха АВ расположено параллельно ОХ. В этом случае плоскость ZOY перпендикулярна лезвию, следовательно, след сечения этой плоскостью лемешно-отвальной поверхности – дуга 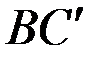 может быть представлена в качестве направляющей кривой.
может быть представлена в качестве направляющей кривой.
Пусть произвольная точка m находится на дуге 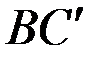 . Через эту точку можно провести горизонтальную и касательную плоскости. Горизонтальная плоскость пройдет через прямую mF,которая является одной из образующих. Для цилиндрического отвала mF параллельна АВ. Эта же горизонтальная плоскость пересечет пласт по линии FK//АО. Очевидно, что угол KFm = g0. Касательная плоскость будет соприкасаться с отвалом по всей линии mF. Пусть двугранный угол между касательной плосостью и дном борозды будет обозначен Q. Угол между гранью отваленного пласта и горизонтальной плоскостью ранее уже был обозначен d. Чтобы установить связь между углами Q, d, g и i из точки F некоторым радиусом, который считают единичным, описывают сферу.
. Через эту точку можно провести горизонтальную и касательную плоскости. Горизонтальная плоскость пройдет через прямую mF,которая является одной из образующих. Для цилиндрического отвала mF параллельна АВ. Эта же горизонтальная плоскость пересечет пласт по линии FK//АО. Очевидно, что угол KFm = g0. Касательная плоскость будет соприкасаться с отвалом по всей линии mF. Пусть двугранный угол между касательной плосостью и дном борозды будет обозначен Q. Угол между гранью отваленного пласта и горизонтальной плоскостью ранее уже был обозначен d. Чтобы установить связь между углами Q, d, g и i из точки F некоторым радиусом, который считают единичным, описывают сферу.
Горизонтальная, касательная плоскости и поверхность пласта пересекутся сферой по дугам КЕ, ЕJ и KJ, которые образуют косоугольный сферический треугольник EKJ. Угол при вершине К не что иное, как δ, при вершине Е равен θ, в при вершине J равен двухгранному углу i.
На основании теоремы косинусов для сферического треугольника
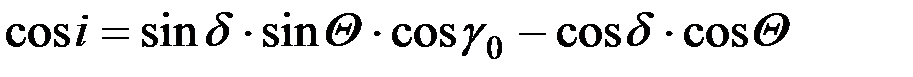 . (1.9)
. (1.9)
Поскольку из условия незадираемости i ≤ 90°, то cos i ≥ 0, тогда из уравнения (1.9) следует
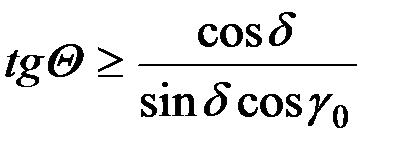 . (1.10)
. (1.10)
Если учесть, что
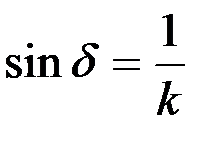 ,
, 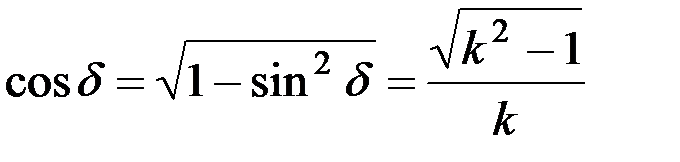 ,
,
то
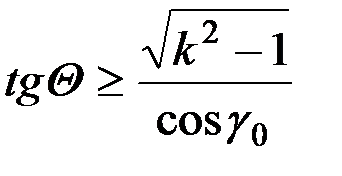 . (1.11)
. (1.11)
Следовательно, во всех случаях, когда касательные к отвалу плоскости окажутся наклонными к горизонту под углом θ, удовлетворяющим условно (1.11), угол i ≤ 90°.
Но угол Q меняется с перемещением точки m по направляющей кривой, т.е. Q = f(z).
Связь между z и θ может быть установлена (рис.1.19а)
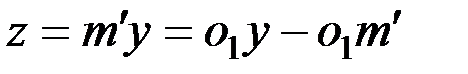 .
.
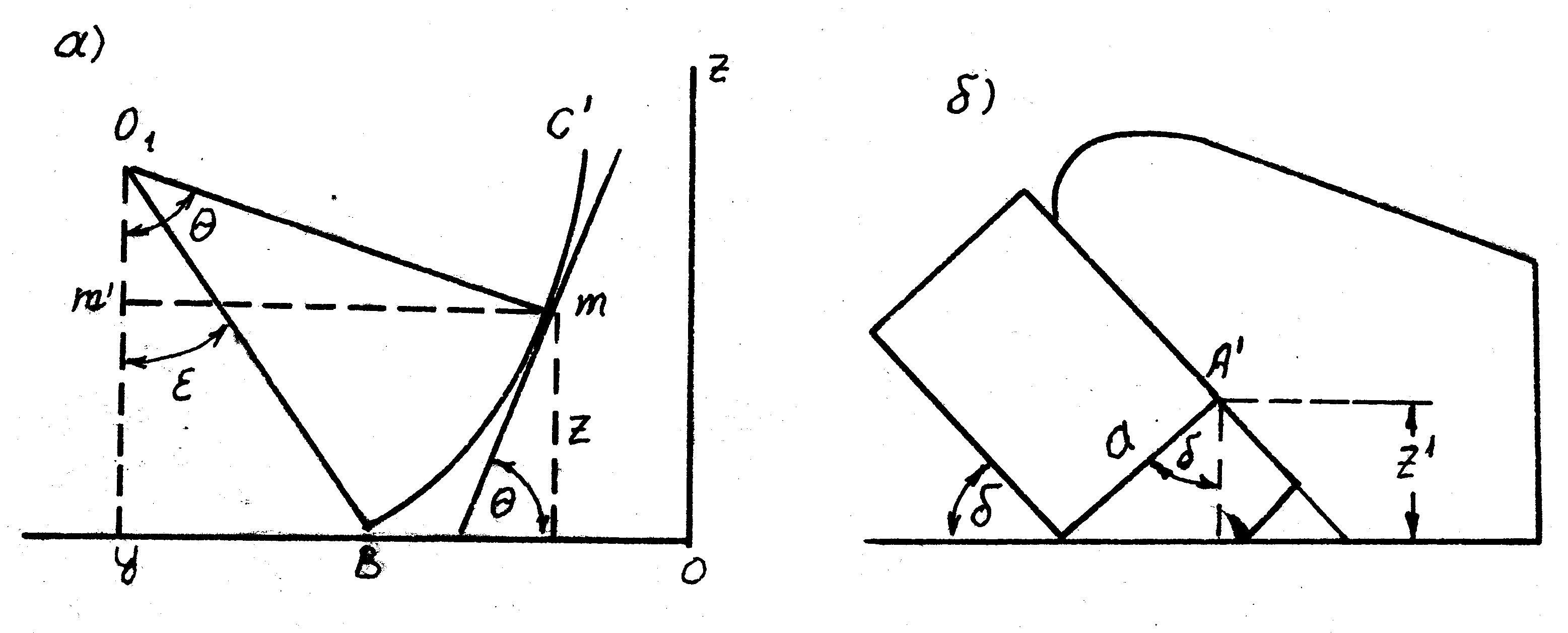
Рис.1.19. Схема к обоснованию максимального значения радиуса направляющей кривой
Но так как 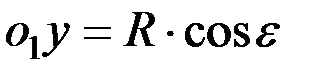 ,
, 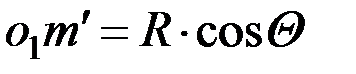 , то
, то
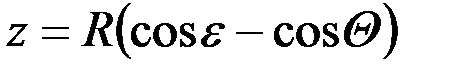 . (1.12)
. (1.12)
Наиболее опасной для задира пласта является точка 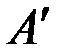 (рис.1.19б). У более высоких точек за счет подгиба крыла вероятность задира уменьшается.
(рис.1.19б). У более высоких точек за счет подгиба крыла вероятность задира уменьшается.
Высота точки 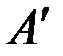 определяется как
определяется как
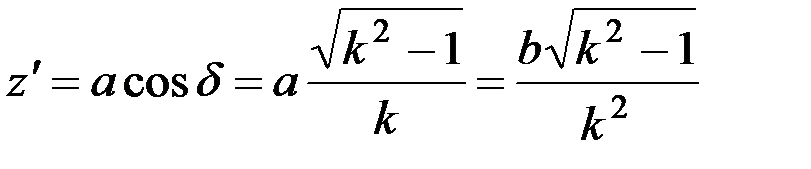 . (1.13)
. (1.13)
Поскольку в точке 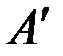 нужно иметь угол i < 90°, то необходимо приравнять z (по уравнению 1.12) и
нужно иметь угол i < 90°, то необходимо приравнять z (по уравнению 1.12) и 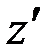 :
:
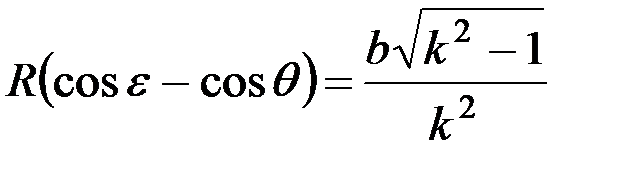 ;
;
отсюда
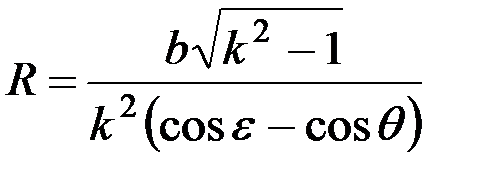 . (1.14)
. (1.14)
Если R увеличить, то кривизна направляющей кривой уменьшится и угол Q в точке 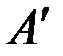 перестает удовлетворять условию (1.11). Таким образом, R по уравнению (1.14) является максимально возможным значением, т.е.
перестает удовлетворять условию (1.11). Таким образом, R по уравнению (1.14) является максимально возможным значением, т.е.
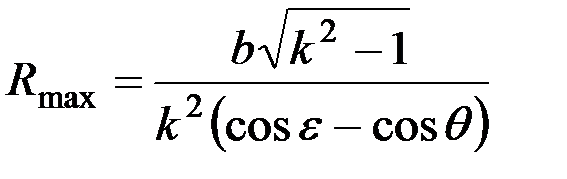 ,
,
где
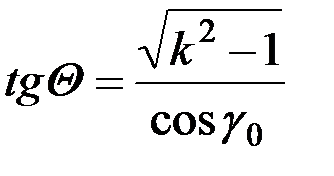 . (1.15)
. (1.15)
От величины радиуса направляющей кривой зависит и высота всей лемешно-отвальной поверхности, так как дуга (направляющая кривая) ограничена центральным углом. На рис.1.19 этот угол составляет 90°-ε, но в действительности он обычно бывает больше. Для обеспечения подгиба крыла, необходимого для лучшего оборота пласта, этот угол увеличивают на Δε, который у поверхностей культурного типа составляет 5...7°, а полувинтового - 8...12° (рис.1.20).
Высота расположения верхней точки А равна
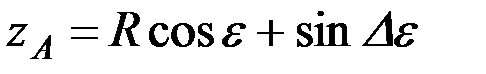 .
.
Только на этой высоте осуществлен подгиб поверхности относительно горизонтали, что может обеспечить угол оборота пласта больше 90°. Но угол β>90° требуется обеспечить на высоте равной b, так как при угле β=90° пласт лишь становится на короткую грань, и чтобы обеспечить дальнейший его оборот на высоте b, необходимо воздействовать на него клином с углом β>90°. Итак, zA=b, отсюда
4 
или
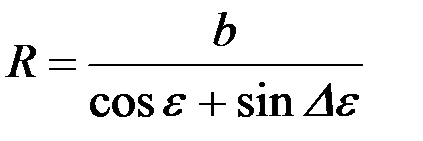 . (1.16)
. (1.16)
Иногда высоту zA называют высотой направляющей кривой. В действительности это не так, поскольку высота направляющей кривой принципиально не может отличаться от Нmax. Поэтому в промежутке высот от zA до Нmax направляющую кривую продолжают по касательной в точке А.
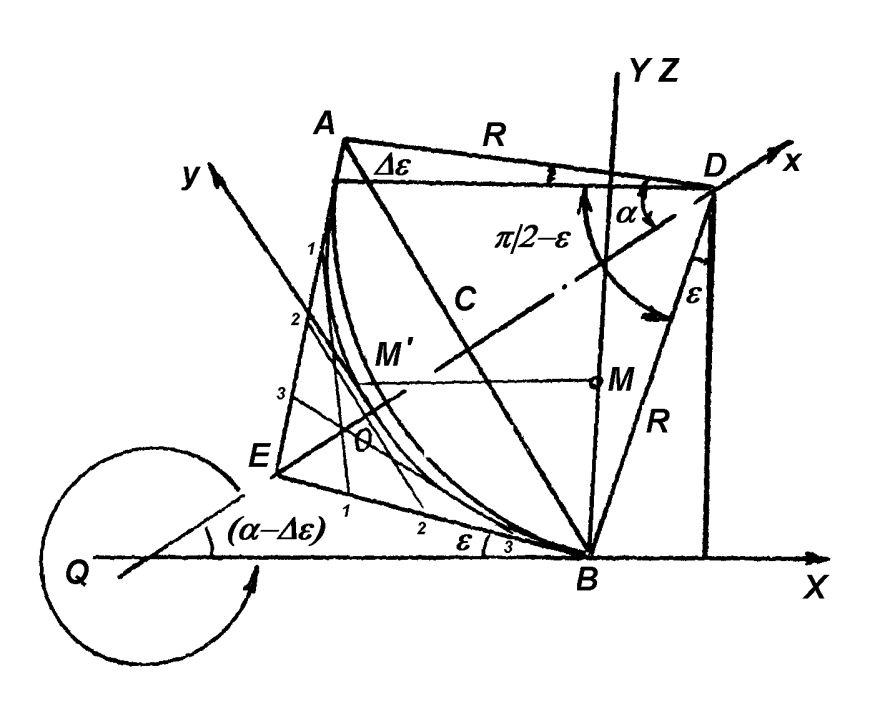
| Рис.1.20. Направляющая кривая |
Дуга окружности не может считаться удовлетворительной формой кривой, служащей направляющей для лемешно-отвальной поверхности, так как имеет постоянную кривизну, что не способствует крошению пласта.
Обычно в качестве направляющей кривой берут параболу, построенную на основе дуги окружности (рис.1..).
Аналитическое исследование технологических свойств лемешно-отвальной поверхности потребовало определение уравнения параболы.
Подробный вывод этого уравнения приведен в учебном пособии [3].
Поскольку длина параболы больше длины дуги окружности, да кривая имеет дополнение в виде подгиба с центральным углом Δε и касательной до высоты Нmax, то подрезанный пласт может разместиться и на направляющей кривой несколько меньше радиуса, чем Rmin по уравнению (1.6).
Дополнительное исследование этой возможности, проведенное в Пермской ГСХА [3] показали, что минимальный радиус может быть сокращен до значения
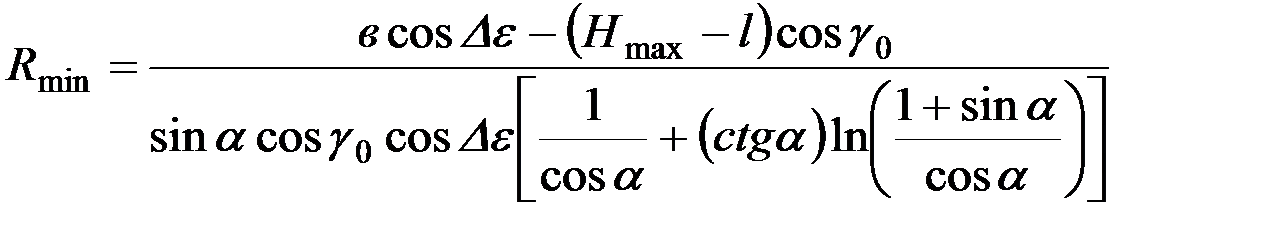 ,
,
где 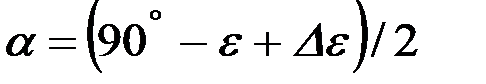 .
.
Это значение радиуса и использовано в компьютерной программе Отвал (otwal), разработанный для проектирования лемешно-отвальной поверхности [3].
1.4. Углы γ образующих со стенкой борозды и законы их изменения
Абсолютное значение углов между образующими и стенкой борозды определяет крошащую способность отвала и сдвиг пласта в сторону. Чем больше углы γ, тем сильнее отвал крошит пласт и дальше сдвигает его в сторону борозды. Правильный выбор угла γ имеет исключительно важное значение для работы плуга. Целый ряд экспериментальных работ, проведенных во Всесоюзном научно-исследовательском институте сельхозмашиностроения, показал, что даже небольшое изменение угла γ0, например с 42°до 40°, приводит к заметному ухудшению крошения почвы. Увеличение угла свыше 45° также делает поверхность неработоспособной из-за того, что почва, сорняки и другие растительные остатки перестают скользить по лезвию (сила трения больше составляющей от силы сопротивления, направленной вдоль лезвия). Таким образом, можно сделать вывод о том, что для отвалов с хорошей крошащей способностью (т.е. чаще всего культурного типа) угол γ0 должен быть ограничен пределами 40...45°, причем крайние пределы даже из этого узкого диапазона используются лишь в исключительных случаях. Полувинтовые плуги имеют меньший угол γ0, порядка 35...40°, что приводит к уменьшению крошащей способности, но это и необходимо, чтобы пласт не разрывался по слабым местам и сплошной лентой укладывался на поле. К этому же результату приводит уменьшение величины сдвига пласта в сторону. Немаловажным является и тот факт, что уменьшение угла γ0 ведет к снижению тягового сопротивления корпуса, так как полувинтовые плуги используют для вспашки задернелых почв.
Дальнейшее снижение угла γ0 невозможно из-за ослабления носка лемеха. При работе на повышенных (8...9 км/ч) и высоких скоростях (9...12 км/ч) корпусы с высокой крошащей способностью испытывают резкое увеличение тягового сопротивления. В то же время крошащая способность отвалов повышается за счет скоростного воздействия орудия на пласт. Снижения тягового сопротивления достигают либо уменьшением угла γ0 до 35...40° (у некоторых видов корпусов), либо за счет уменьшения угла постановки лемеха к дну борозды (23...25° по сравнению с 30° у поверхности культурного типа). Таким образом, у скоростных плугов угол γ0 варьируют в широких пределах (35...45°).
У поверхностей цилиндроидального типа угол γ не остается постоянным для всех образующих, а меняется с ростом высоты расположения образующих по определенному закону (рис.1.21, 1.22, 1.23). Закономерности изменения углов для поверхностей различного типа определены с учетом особенностей условий работы каждого корпуса, но имеют и некоторые общие свойства. Прежде всего это увеличение углов γmax по сравнению с γ0 в верхней части отвала. Как уже было отмечено выше (рис.1.11), это сделано для улучшения условий оборота пласта.
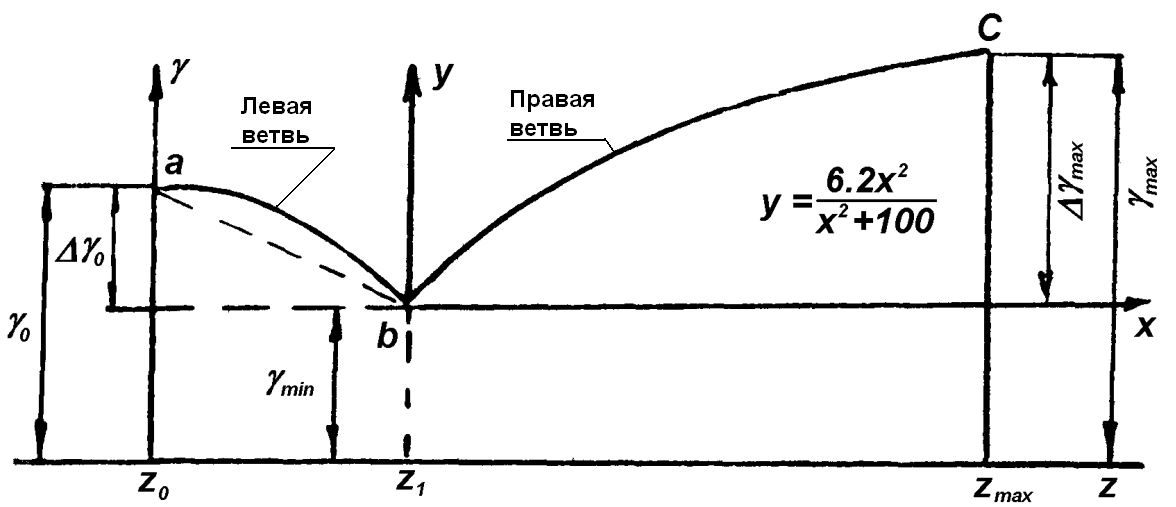
Рис.1.21. Закономерность изменения угла γ у лемешно-отвальной поверхности культурного типа
Второй особенностью является уменьшение угла γ от γ0 до γmin на высоте Z1. Необходимость уменьшения угла на начальном участке закономерности γ=f(z) вызвана стремлением способствовать уменьшению опасности задирания на нижней части обрабатываемого пласта почвы.
Закономерности изменения углов γ в зависимости от высоты расположения образующих подобраны эмпирически, на основе анализа лучших отвалов того или иного назначения.
Для поверхности культурного типа, обеспечивающей хорошее крошение старопахотных почв рекомендуется [ ] в качестве закономерности γ = f(z) использовать параболу вида
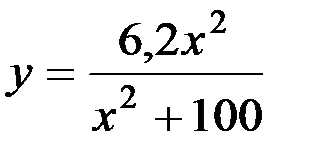 , (1.17)
, (1.17)
где х - абсцисса параболы, измеренная в сантиметрах и определяющая расстояние от z1 до анализируемой образующей, находящейся на высоте z, т.е.
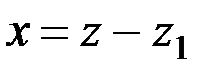 ;
;
y - величина изменения углов γ, выраженная условно в сантиметрах, т.е.
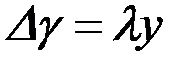 .
.
В этом уравнении 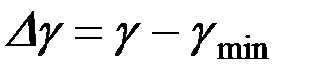 , а γ - величина масштабного коэффициента, зависящего от пределов изменчивости углов γ.
, а γ - величина масштабного коэффициента, зависящего от пределов изменчивости углов γ.
Поскольку эти пределы для левой (z меняется от 0 до z1) и право й ветвей параболы
(участок z от z1 до zmax) отличаются друг от друга, то и масштабы λ1 и λ2 окажутся различными, а именно:
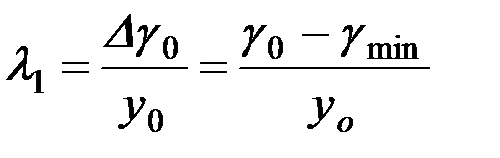 , (1.18)
, (1.18)
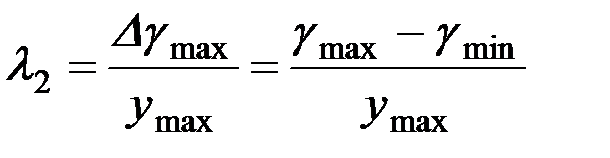 . (1.19)
. (1.19)
Значения y0 и ymax рассчитываются по уравнению (1.17) с учетом значений
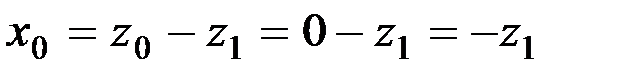 ;
;
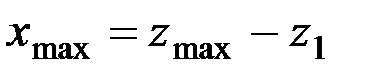 .
.
Например, для корпуса К - 35 характерны следующие параметры: γ0=42°, γmin=40°, γmax=47°, z1=7,5 см, zmax=43,5 см.
Для левой ветви параболы
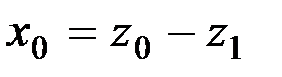 ,
, 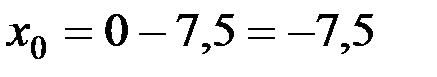 см;
см;
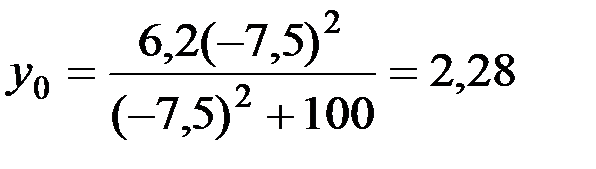 , см;
, см;
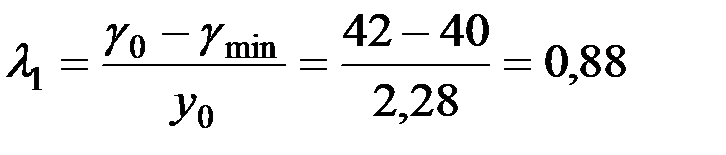 град/см.
град/см.
Промежуточные значения угла γ1 для образующей, расположенной на высоте z1, для левой ветви вычисляют как
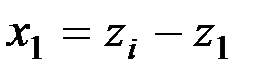 ;
;
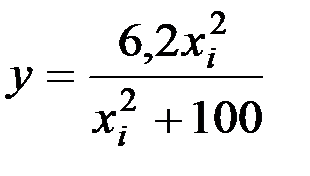 ;
;
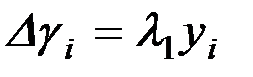 ;
;
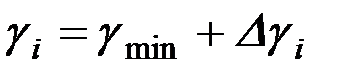 . (1.20)
. (1.20)
Для правой ветви
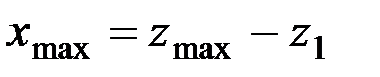 ,
, 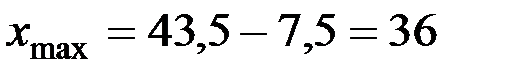 см;
см;
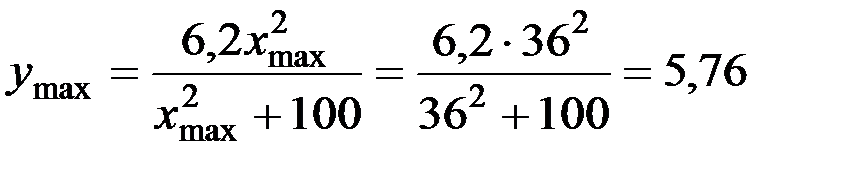 см;
см;
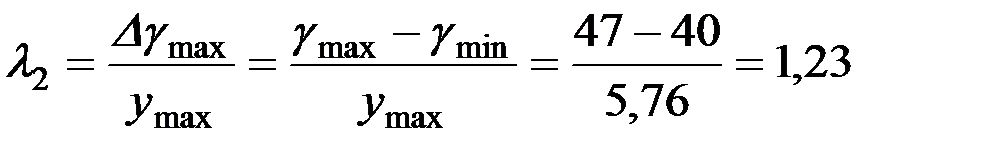 град/см.
град/см.
Вычисление промежуточных значений углов γ1 для правой ветви ведется аналогично (1.20), т.е.


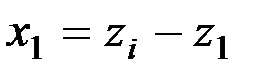 ,
, 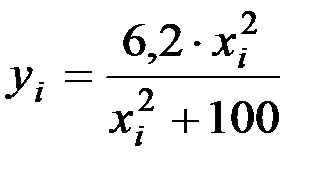 ,
,
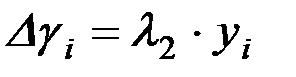 ,
,
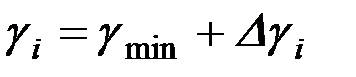 . (1.21)
. (1.21)
Особенностью данной закономерности является интенсивное развитие угла γ в зоне груди отвала, где осуществляется крошение обрабатываемого пласта.
Закономерности изменения угла γ для полувинтовых отвалов отличаются интенсивным развитием в зоне крыла и верхней части отвала для интенсивного подворота почвы. В зоне груди отвала этот угол нарастает слабо, чтобы исключить возможность разрыва пласта. Изменение угла γ для полувинтовых отвалов составляет 7...12° (рис.1.22).
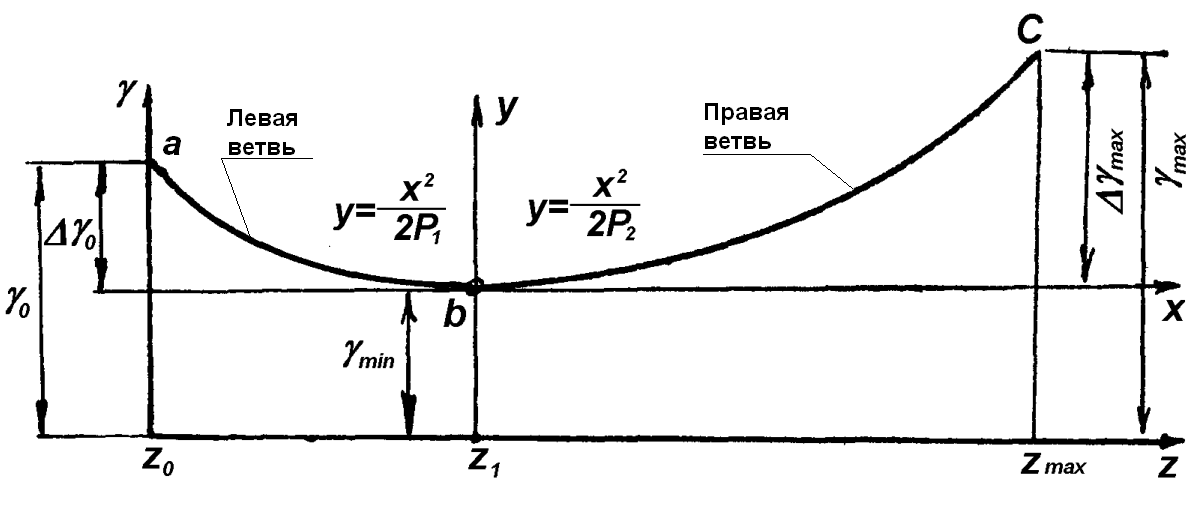
| Рис.1.22. Закономерность изменения угла γ у лемешно-отвальной поверхности полувинтового типа |
Для расчета промежуточных значений углов γ полувинтовых отвалов рекомендуется [2] использовать параболу вида:
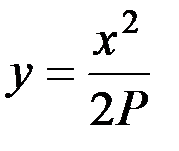 , (1.22)
, (1.22)
где x = z - z 1, 2 Р - параметр параболы.
Параметры Р1 и Р2 для левой и правой ветвей выбирают в зависимости от масштаба λ, с тем чтобы парабола описывала изменения углов в заданных пределах. Поскольку в данном случае необходим выбор и параметра Р и масштаба λ, то одной из этих величин можно задаться. Чаще всего величину масштаба принимают равной 1 град/см.
Для правой ветви
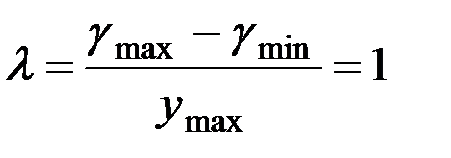 ,
,
или
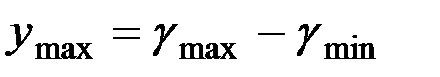 .
.
Расчетным путем по уравнению (1.22) находят
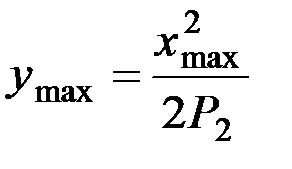 .
.
Поскольку левые части двух последних равенств одинаковы, то можно получить
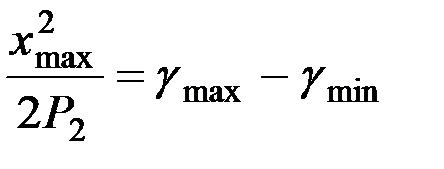 .
.
Отсюда находится величина параметра параболы:
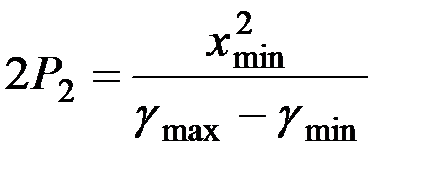 , (1.23)
, (1.23)
где 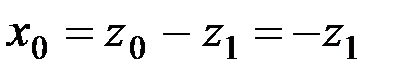 , так как z0 = 0.
, так как z0 = 0.
Например, если задана полувинтовая поверхность с параметрами γ0=38°, γmin=36°, γmax=48°, zmax=40,512см, z1=7,5см, то
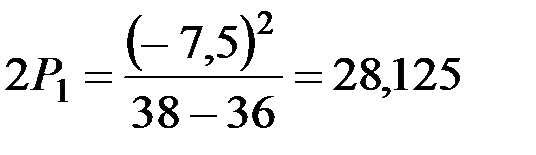 ;
; 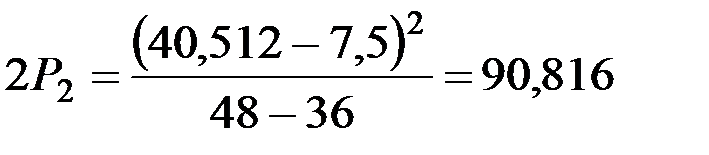 .
.
Угол наклона любой образующей может быть рассчитан. Так, для z=20см, то
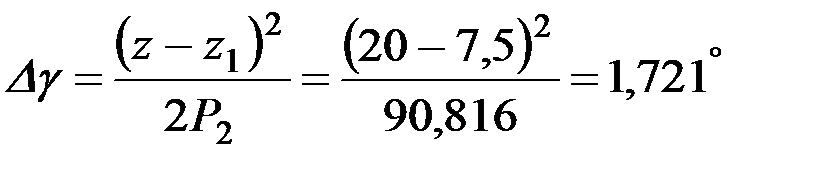 ,
,
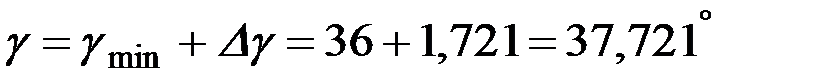 .
.
Закономерности изменения углов γ у скоростных корпусов отличаются большим разнообразием. Так, для работы на скоростях до 9 км/ч могут быть использованы корпусы с культурной лемешно-отвальной поверхностью, у которой угол γ0=38°. На скоростях 8...12 км/ч удовлетворительно работает корпус с поверхностью, представляющей собой цилиндроид с закономерностью изменения углов γ, которая изображена на рис. 1.23.
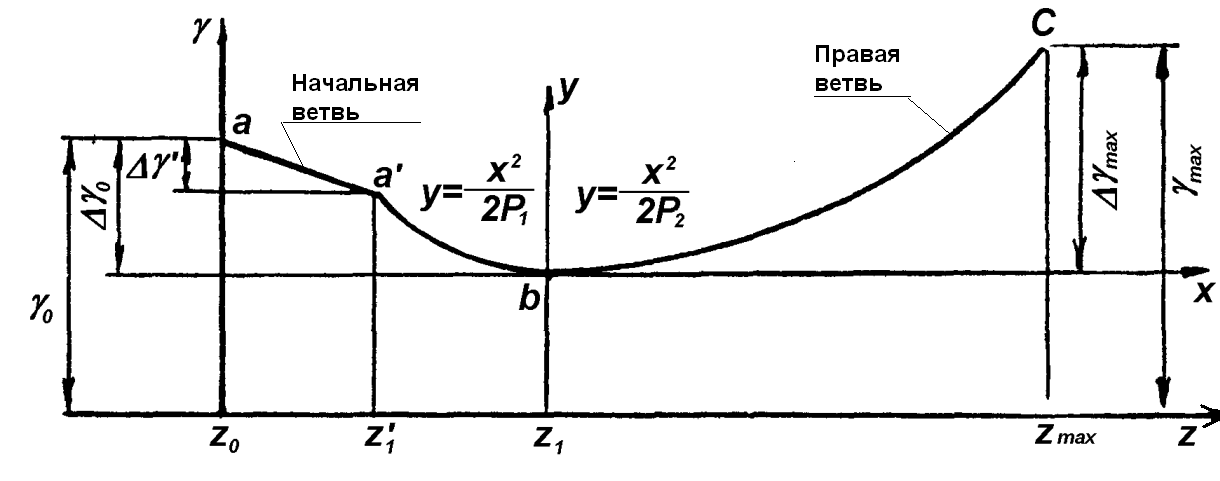
| Рис.1.23. Закономерность изменения угла γ лемешно-отвальной поверхности скоростного корпуса плуга |
Отличительной особенностью данной поверхности является уменьшение углов между образующими и стенкой борозды, происходящее не только в зоне лемеха, но и в зоне лемеха, но и в зоне груди отвала. Благодаря этому достигается пологая установка крыла, в результате чего уменьшается скорость отбрасывания почвы в борозду. Кроме того, при такой закономерности углов обеспечивается сравнительно небольшое давление пласта на рабочую поверхность, которое уменьшается последовательно от лемеха, но и в зоне груди отвала и его крылу.
При расчете промежуточных значений углов γ для образующих, расположенных на различных высотах, необходимо учесть, кроме правой и левой ветвей параболы, участок, на котором угол меняется по линейному закону (так называемая начальная ветвь закономерности).
Промежуточные значения углов определяют на этом участке по простой зависимости:
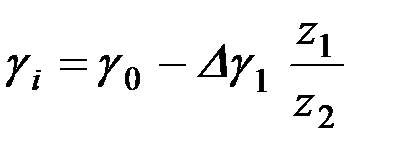 , (1.25)
, (1.25)
где 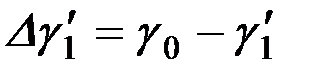 - изменения углов γ в конце начальной ветви;
- изменения углов γ в конце начальной ветви;
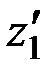 - высота расположения начальной ветви.
- высота расположения начальной ветви.
На участке высоты от 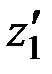 - до
- до 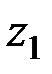 (левая ветвь параболы) параметр параболы может быть вычислен как:
(левая ветвь параболы) параметр параболы может быть вычислен как:
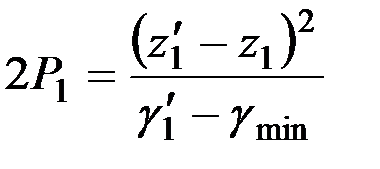 (1.26)
(1.26)
где 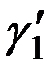 - угол γ в конце начальной ветви.
- угол γ в конце начальной ветви.
Промежуточные значения углов γ определяют по формуле
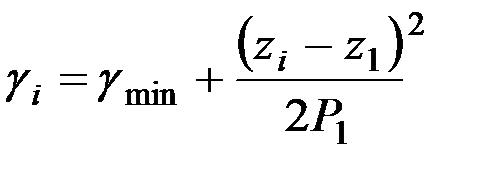 . (1.27)
. (1.27)
Для правой ветви параболы соответственно:
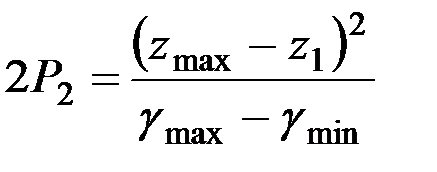 , (1.28)
, (1.28)
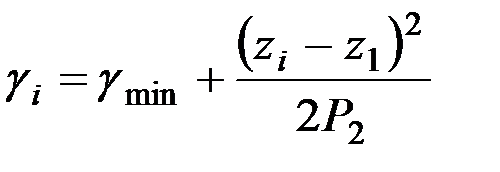 . (1.29)
. (1.29)
Расчет параметров лемешно-отвальных поверхностпей может быть осуществлен с помощью компьютерной программы "Отвал" (Otwal). Пример использования этой программы приведен в учебном пособии [3].
Проектирование поверхности отвала рассмотрено в учебно-методическом пособии [4].
Контрольные вопросы
1. Рабочая поверхность плуга как развитие косого трехгранного клина. Способы образования лемешно-отвальной поверхности.
2. Условие устойчивости пласта почвы, отваленной плугом.
3. Обоснование радиуса Rmin для направляющей кривой.
4. Обоснование величины Rmax направляющей кривой.
5. Закономерности изменения углов γ между образующими и стенкой борозды у цилиндроидальных поверхностей корпусов плугов.
Литература
1. Горячкин В.П. Отвал. К графической теории плуга. Собрание сочинений. Т.2. М.: Колос. 1965 - 495 с.
2. Циммерман М.З. Рабочие органы почвообрабатывающих машин. М.: Машиностроение, 1978.
3. Кошурников А.Ф. и др. Анализ технологических процессов, выполняемых сельскохозяйственными машинами, с помощью ЭВМ. Пермь, 1995, 272 с.
4. Кошурников А.Ф. Проектирование рабочей поверхнорсти корпуса плуга цилиндроидального типа с использованием результатов расчета параметров на ЭВМ. Пермь. ГСХА, 2010 - 37с.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1997; Нарушение авторских прав?; Мы поможем в написании вашей работы!