Определение коэффициентов формулы В.П. Горячкина на основе опытных данных

Для определения формулы необходимо определить коэффициенты. Наиболее точно она могут быть найдены после многократных опытов по динамометрированию плуга в поле на различных скоростях при изменяемой глубине пахоты. После этого экспериментальные данные обрабатывают по так называемому способы наименьших квадратов, суть которого состоит в том, что наиболее вероятными значениями f,k и ε будут те, которые приведут к минимальным значениям сумму квадратов разности между расчетными и опытными данными.

В каждом опыте между экспериментальным значением Р и расчетной величиной, определяемой уравнением (2.4), будет обнаружено некоторое отклонение δ, т.е.

.

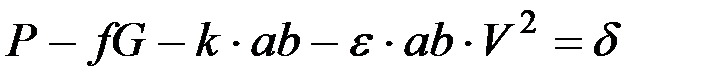Если правую и левую части уравнения возвести в квадрат, то

.

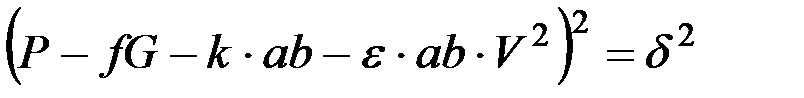После суммирования квадратов отклонений по всем опытам получится

.

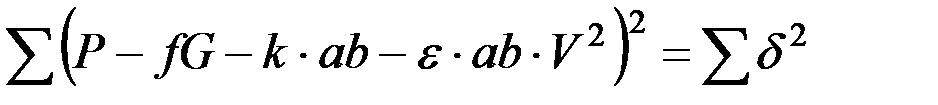В этом уравнении неизвестными являются коэффициенты f, k, ε, а все остальные величины должны быть зафиксированы при проведении эксперимента.

Известно, что минимальное значение функции определяют путем приравнивания нулю первой производной. Для отыскивания минимума функций трех переменных необходимо приравнять нулю частные производные по всем переменным и составить систему из трех уравнений:

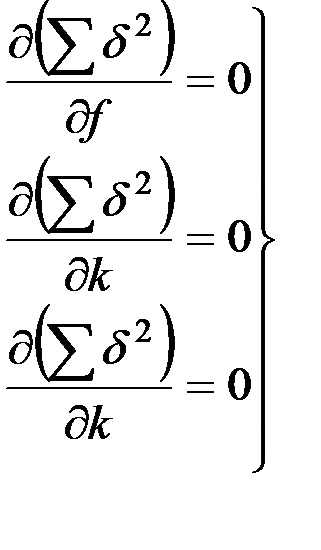, (2.5)

Частная производная по ∂k необходимо также приравнять нулю:

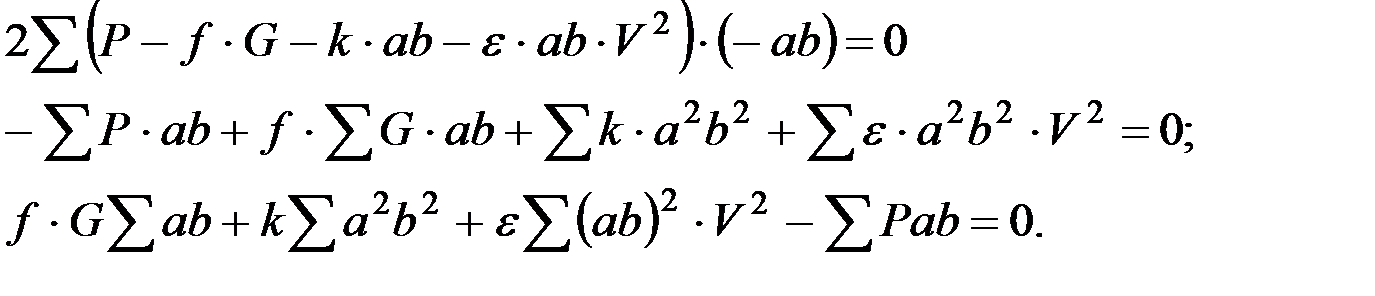
И, наконец,

.

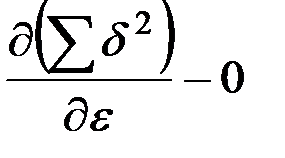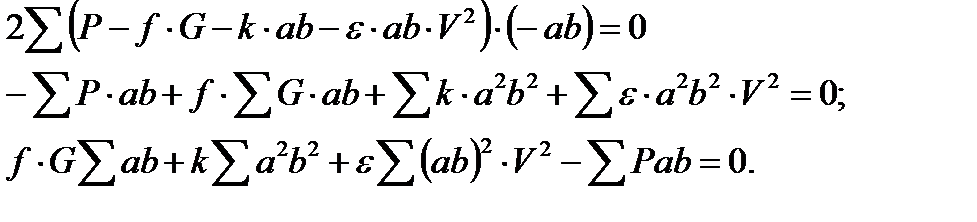
Систему из трех уравнений можно представить так:

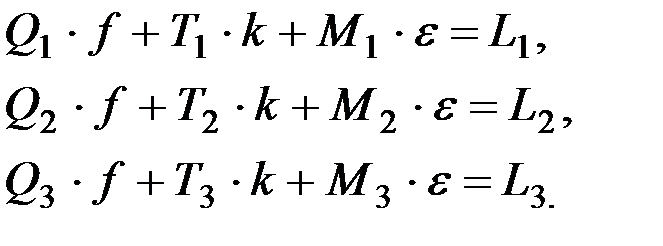(2.6)

где

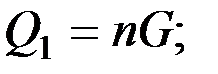
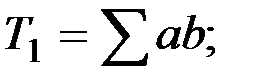
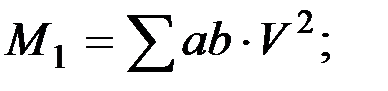
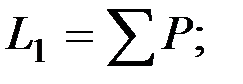
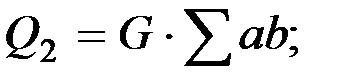
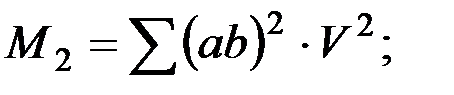
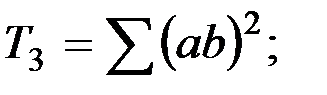
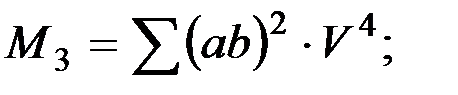
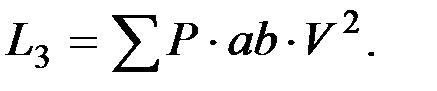(2.7)

Решение системы уравнений (2.6) можно осуществить по методу Крамера:

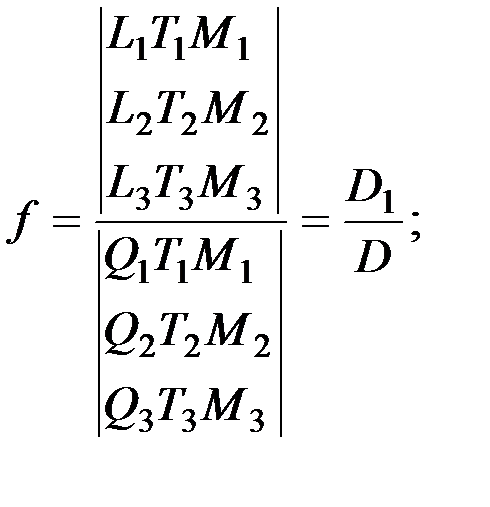
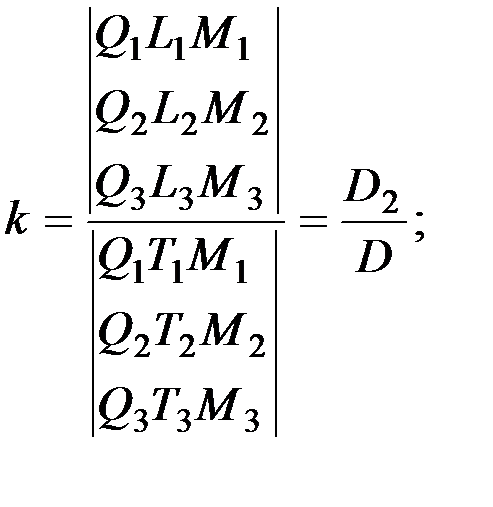
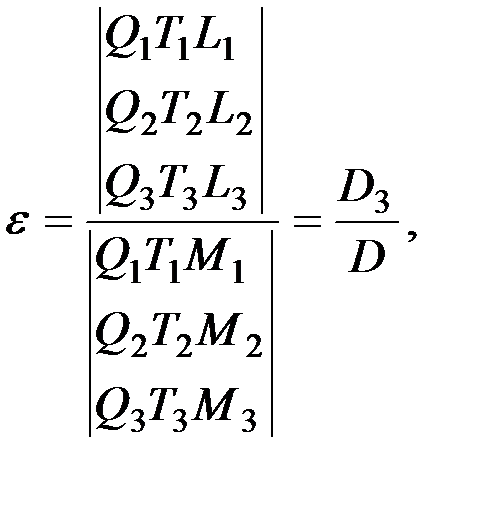
где D - определитель, составленный из коэффициентов перед неизвестными в системе (2.6);

D₁ - определитель, у которого коэффициенты перед f заменены свободными членами;

D₂ - определитель, у которого коэффициенты перед k заменены свободными членами;

D₃ - определитель, у которого коэффициенты перед ε заменены свободными членами.

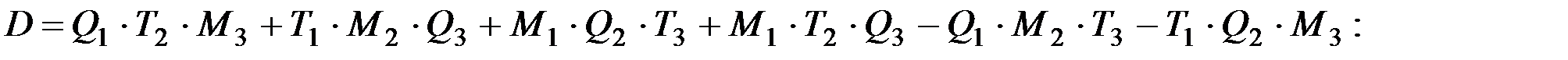
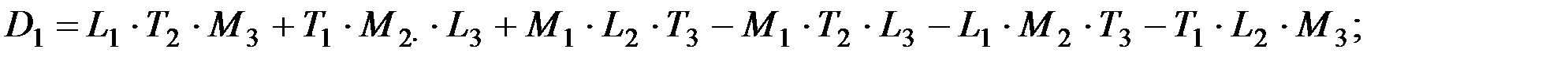
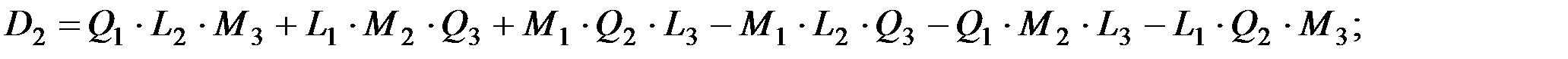
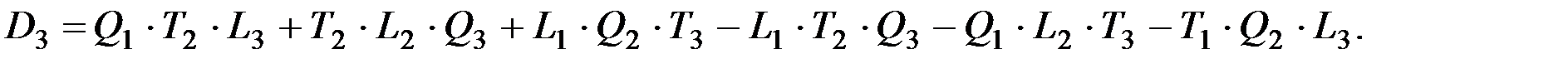
Окончательно коэффициенты находятся так:

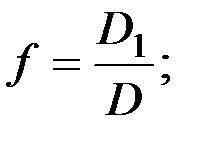
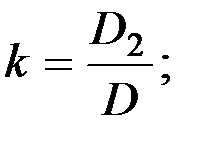
(2.9)

Попытки вычислений всех трех коэффициентов из многократных динамометрирований плугов при помощи способа наименьших квадратов оказались очень сложными, громоздкими и для широкого применения малопригодными во всяком случае до широкой компьютеризации.

Вычисления значительно упрощаются, если один из коэффициентов f определит независимо от остальных, например динамометрированием плуга, протаскиваемого по заранее открытой борозде. Разумеется, что сопротивление Р₁ в этом случае определяется с некоторым приближением, но практический опыт показал, что отличия , определенные по той или иной методике не очень существенно.

В качестве примера могут быть приведены результаты расчетов при обработке опытов по определению рабочего сопротивления плуга ПЛН-4-35, проведенных в учхозе «Липовая Гора» Пермской ГСХА.

Всего проведено 20 измерений силы тяги при различной скорости, глубине обработки и ширине пласта. Кроме этого проведено определение составляющей путем протаскивания плуга по заранее открытой борозде (в соответствии с методикой В.П. Горячкина) [ ].

В соответствии с этой методикой существенно снижается трудоемкость расчетов, и тем самым повышается наглядность применения способа наименьших квадратов.

Если усилие Р₁ определено заранее, то отклонение δ между экспериментальной и расчетной частями уравнения (2.4) может быть представлено в виде:

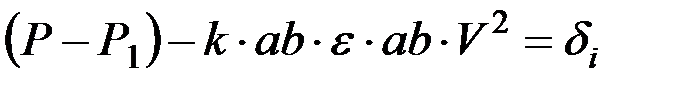, (2.10)

или

(2.11)

поскольку a и b в каждом опыте измерена.

Уравнение, определяющее сумму квадратов отклонений преобразуется к виду

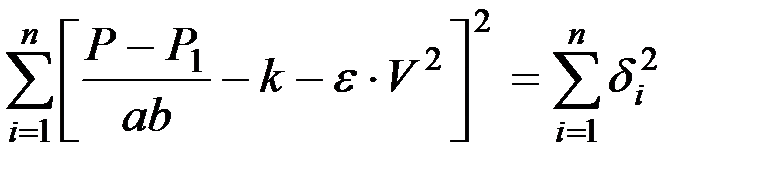. (2.12)

Минимальное значение этой функции может быть определено решением системы двух уравнений

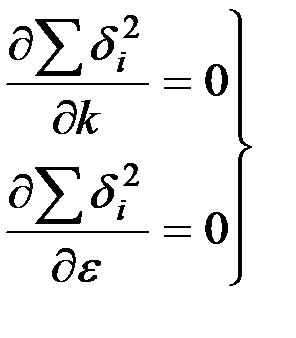. (2.13)

Частная производная 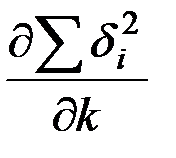будет равна

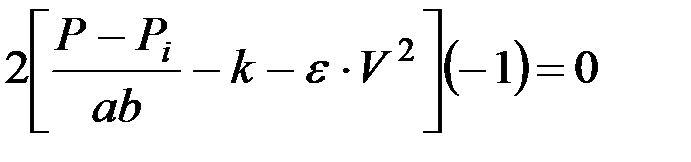
или

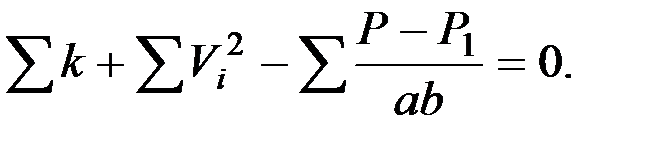
и если ввести обозначения 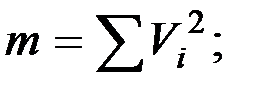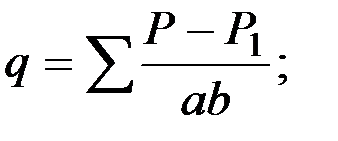то .

Совершенно аналогичным можно определить и другую частную производную

или

,

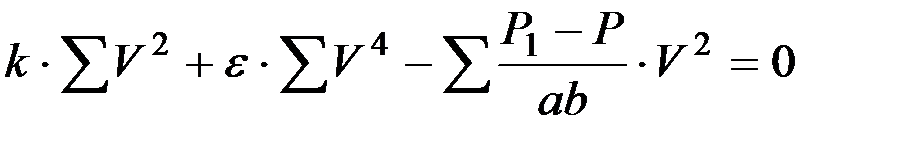или

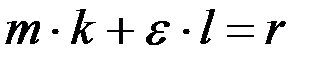, (2.15)

если ввести обозначения ; .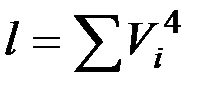

Решение системы уравнений (2.14) и (2.15)

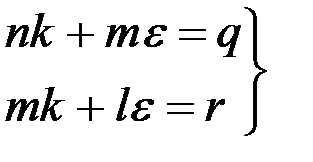
может быть осуществлено по методу Крамера

; ,

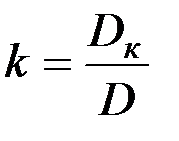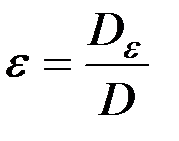где D - определитель из коэффициентов перед искомыми величинами, а в определителях D_к и D_ε соответствующие коэффициенты определителей замещаются свободными членами, т.е.

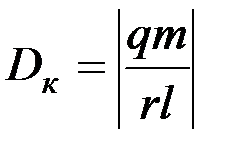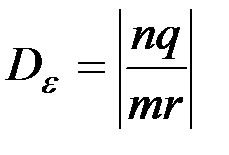; ; . (2.15)

Для иллюстрации метода расчета в таблицу записи и обработки опытных данных внесены результаты первых четырех опытов.

№ опыта	V	V^2	V^4	a,	b,	ab	P1	P1	P-P1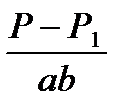
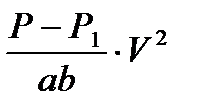
	2.00	4.00	16.00	0.24	1.41	0.338				2603.55	10414.20
	2.01	4.04	16.32	0.25	1.42	0.355				2605.63	10526.76
	2.02	4.08	16.65	0.255	1.40	0.357				2610.64	10651.43
	2.10	4.41	19.45	0.23	1.39	0.320				2659.38	11727.84
Σ		m=16.53	l=68.42							q=10479.20	r=43320.23

Определители (2.15) окажутся соответственно равными:

.

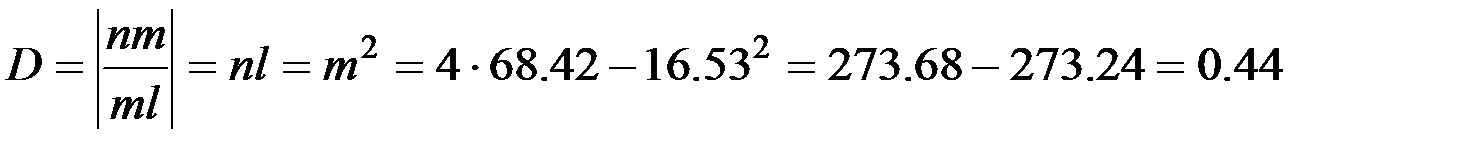
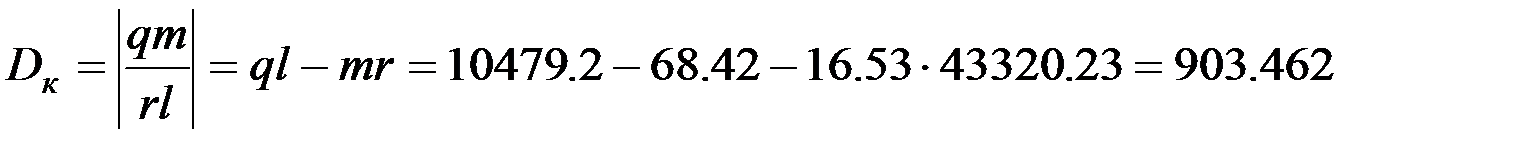
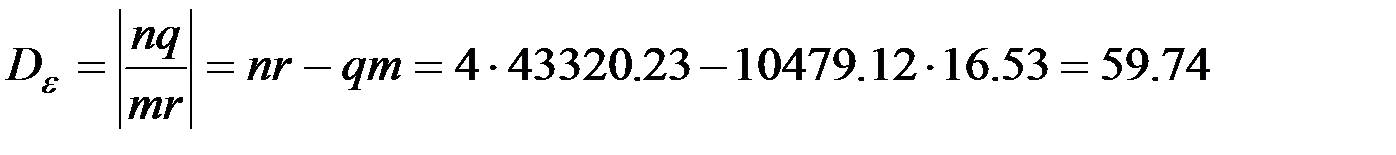Коэффициенты рациональной формулы В.П. Горячкина окажутся следующими:

; ; .

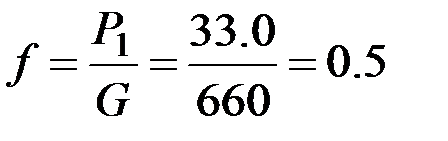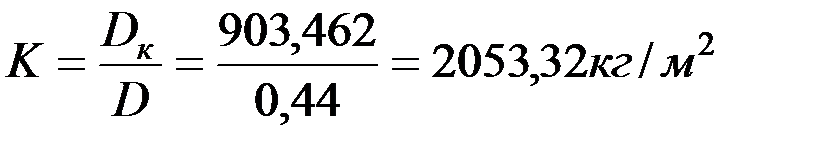Расчеты на компьютере по программе "Рацфор" с учетом всех 20 опытов и определителей третьего порядка (2.8) привели к следующим результатам:

f=0.502; k=1996.301кг/м²; ε=150,126кг.с/м⁴.

Эти значения характерны для легких почв.

В.П. Горячкин, исследовавший плуги в различных почвенных условиях достаточно скрупулезно (до 81 измерений на каждом фоне), получил следующие значения коэффициентов:

f=0.5 для жнив... и f=1 для клеверища; k=2000 кг/м² на легких почвах, 3000 кг/м² на средних и 4000...5000 кг/м² - на тяжелых; ε = 150...200 кг.с²/м⁴.

Контрольные вопросы

1. В чем состояла необходимость установления связи между рабочим сопротивлением плуга и такими факторами, как глубина обработки, ширина пласта и скорость агрегата?

2. Какие гипотезы использованы при установлении зависимости P=f(a,b,V_i, G_пл)?

3. Сформулируйте суть метода наименьших квадратов.

4. Как используется метод Крамера при определении коэффициентов рациональной формулы В.П. Горячкина.

Литература

1. Горячкин В.П. Собрание сочинений. Т.2. М.Колос, 1965.

2. Турбин Б.Г. Сельскохозяйственные машины. Л. Машиностроение, 1967.

3. Кошурников А.Ф. и др. Анализ технологических процессов, выполняемых с.-х. машинами с помощью ЭВМ. Пермь, 1995, 272 с.

Дата добавления: 2015-06-04