Обоснование параметров сферических дисков

Классификация и характеристика основных типов дисковых орудий

Обоснование основных параметров дисковых рабочих органов почвообрабатывающих машин

По назначению дисковые орудия подразделяются на плуги, лущильники и бороны. Дисковые плуги используются для вспашки переувлажненных, тяжелых и твердых почв. Рабочим органом плуга является сферический диск, смонтированный на специальном кронштейне. Прицепные плуги снабжают дисками диаметром 610...810 мм, навесные 580...710 мм. Плоскость лезвия диска образует с направлением движения угол атаки 40...45° и с вертикальной осью 15...25°. Для лучшего оборота пласта и очистки диска от налипающей почвы применяют короткие отвальцы (рис. 6.1).

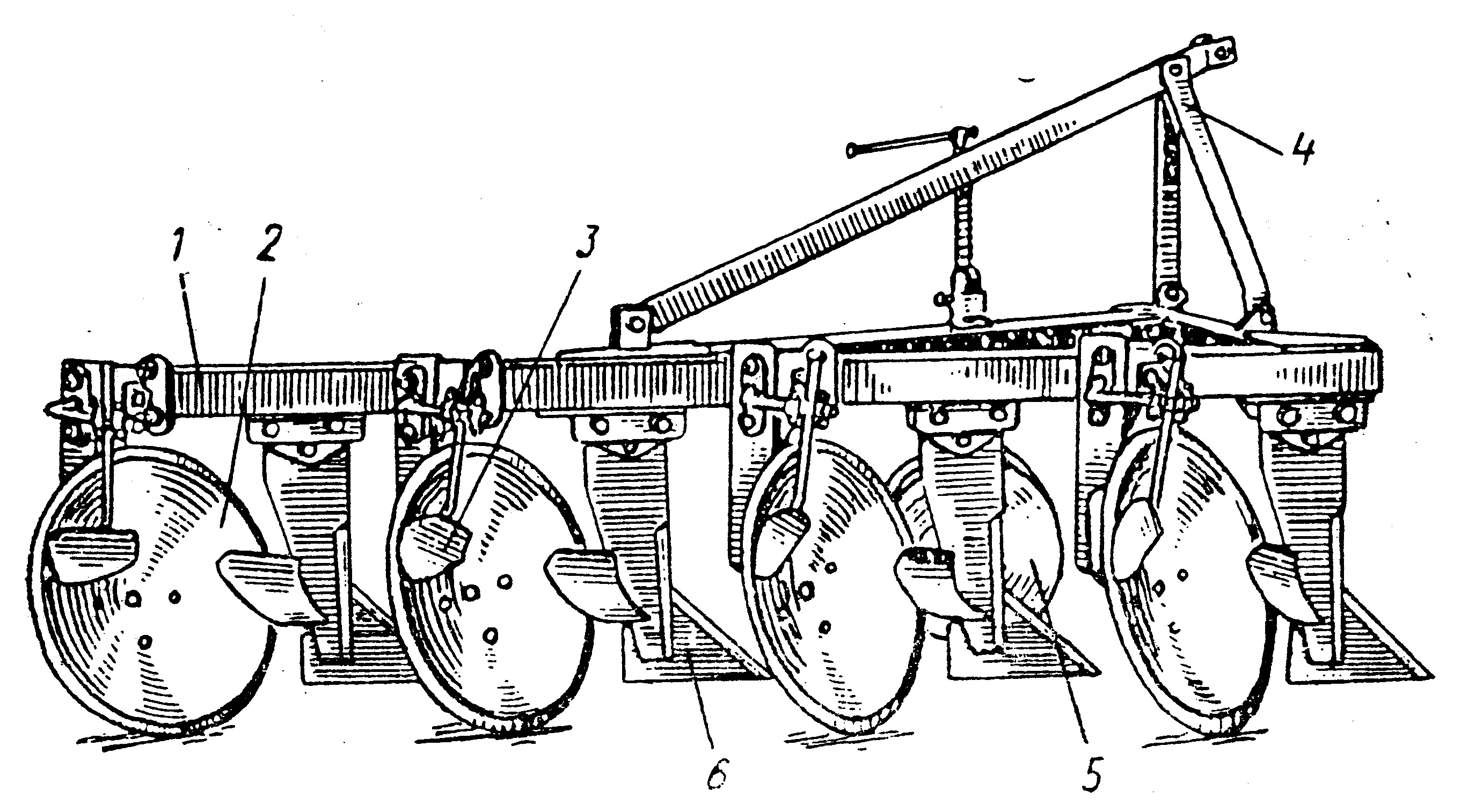
Рис. 6.1. Навесной дисковый плуг ПНД-4

1 – рама; 2 – дисковый корпус; 3 – чистики-отвальцы; 4 – навесное устройство; 5 опорное колесо; 6 - предплужники с полевыми досками и рыхлителями

Дисковые бороны по назначению делят на полевые, садовые и болотные (тяжелые).

Полевые дисковые бороны применяют для измельчения задернелых пластов и глыб на поверхности вспаханного поля, весенней предпосевной обработки зяби, а в некоторых случаях для культивации паров, лущения стерни и освежения лугов. Глубина обработки составляет 6...10 см, диаметр дисков 450...500 мм, расстояние между дисками 165...180 мм, угол атаки β = 10...22°. Как правило, бороны делают двухследными. Наибольшее распространение среди борон этого типа получили машины БДТ-3,0 и БДТ-7,0 (рис. 6.2).

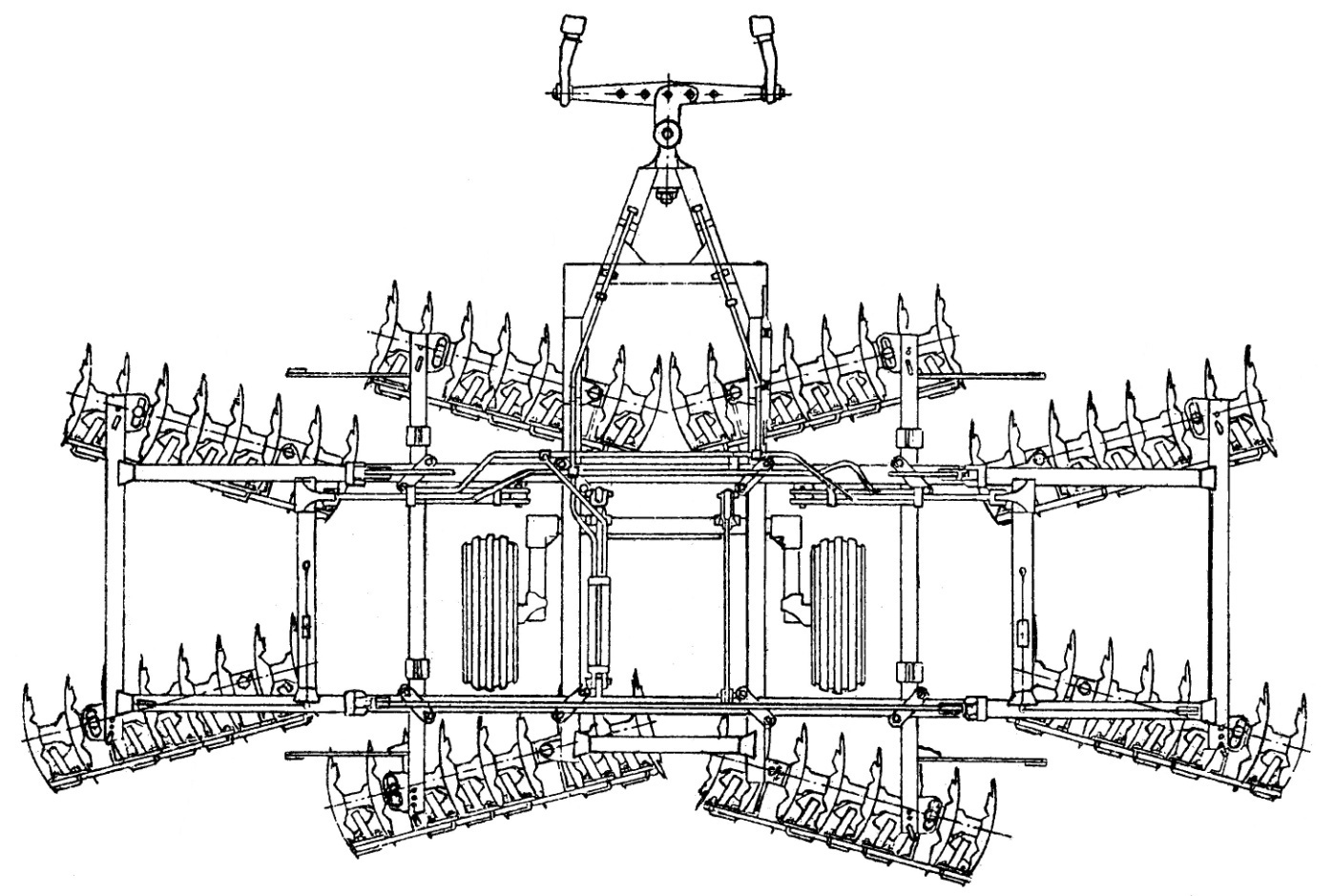
Рис. 6.2. Борона дисковая тяжелая БДТ-7

Дисковые лущильники применяют в основном для лущения стерни на глубину 6...10 см, поскольку дисковое орудие меньше подвержено забиванию соломкой, сорняками и другими волокнистыми материалами. В настоящее время их стали применять и для других сельскохозяйственных операций, в частности, для предпосевной обработки, обработки паров, закрытия влаги. Семейство современных гидрофицированных лущильников включают в себя ЛДГ-5, ЛДГ-10, ЛДГ-15, ЛД-20 и ЛДГ-20.

Рабочая поверхность сферического диска совершает сложное движение в пространстве. Кроме поступательного горизонтального перемещения вместе с машиной, диски под действием реактивных сил, действующих со стороны почвы, вращаются вокруг своей оси. Перемещение диска из положения I в положение II (рис.6.8) может быть разложено на две составляющие. Одна из них направлена в плоскости режущей кромки диска по линии 1...1¢, а вторая, перпендикулярная первой, - по линии I¢...II. При движении на участке 1...1¢ диск не только перемещается поступательно, но и вращается вокруг своей оси, в результате чего он совершает движение качения. Если пренебречь возможным скольжением или буксованием диска, то длина пути L¢ вдоль по линии 1...1¢ составит L=πD, где D - диаметр диска. Путь, пройденный диском вдоль направления движения за один оборот, будет равен:

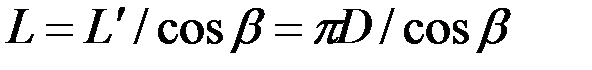. (6.1)

Скорость движения любой точки М лезвия диска может быть определена геометрическим сложением проекции скорости поступательного движения машины на ось диска 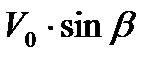и окружной скорости V_окр, выбранной точки лезвия:

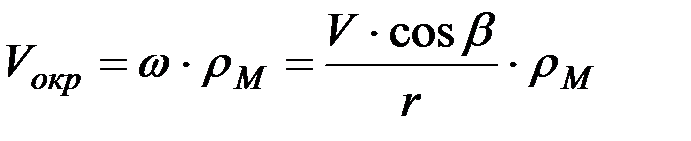. (6.2)

где w - угловая скорость при вращении диска вокруг мгновенного полюса Ω;

ρ_м - расстояние от точки М до полюса;

r - радиус диска.

Траектория движения произвольной точки М лезвия имеет форму винтовой линии, последовательность построения которой показана на рис. 6.3. Аналогичными построениями можно определить движение в почве лезвия вырезных дисков тяжелых борон. На поверхности дна борозды после прохода вырезного диска имеются винтообразные ленты треугольного сечения, что придает борозде некоторое сходство с внутренней частью гайки.

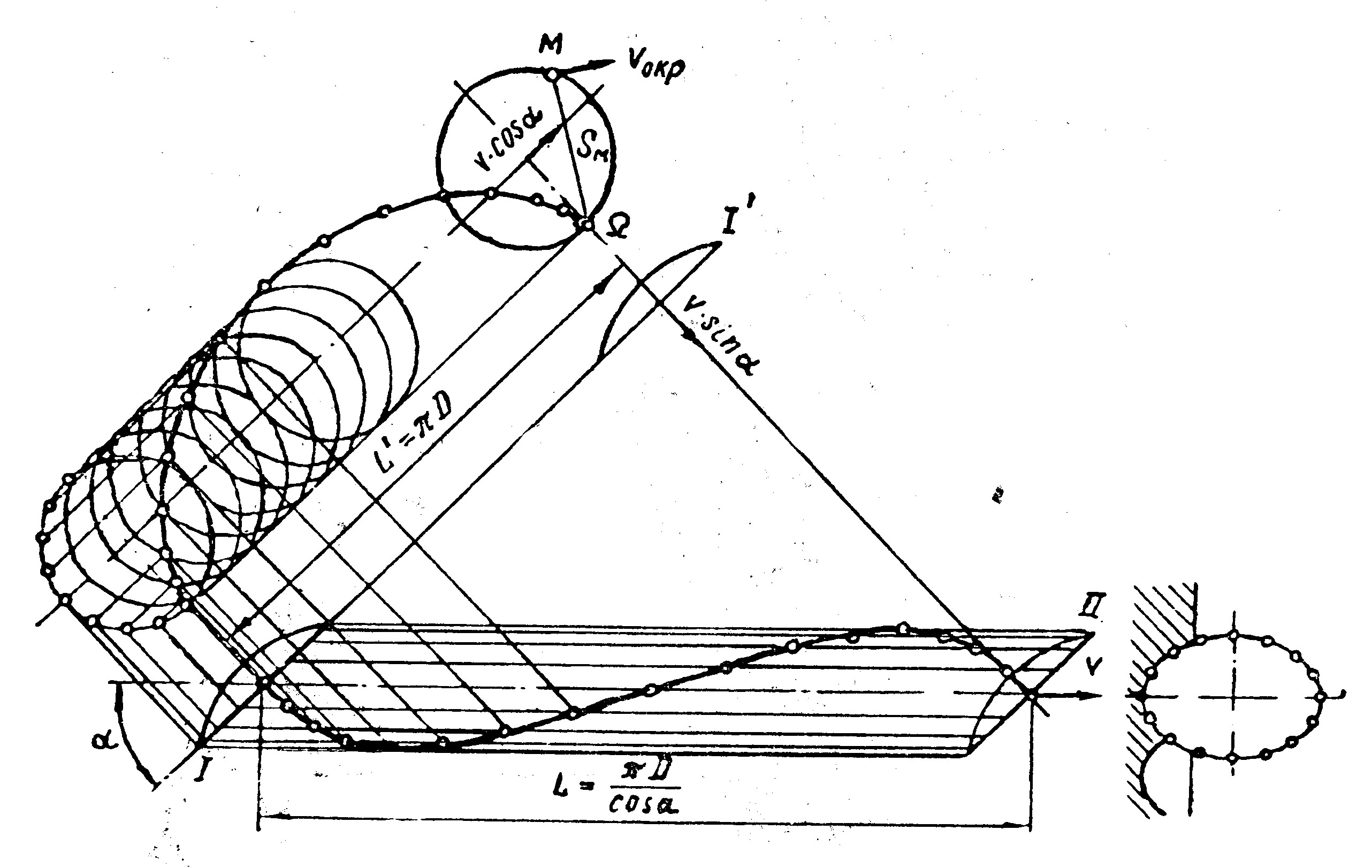
Рис. 6.3. Кинематика дискового рабочего органа

Их уравнений (6.1) и (6.2) следует, что основные характеристики дискового орудия определяются величиной диаметра диска и угла атаки.

Диаметр диска стремятся выбирать наименьшим из допустимых значений. В значительной мере он зависит от заданной глубины обработки почвы:

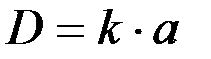, (6.3)

где k - коэффициент (для плугов k = 3...3,5, лущильников - 5...6, борон - 4...6).

Для борон и лущильников при выборе к следует учитывать свойства почвы, так как дернистая, сырая и тяжелая почва может запрессовываться между дисками. Чем тяжелее предполагаемые условия работы, тем больше должен быть коэффициент k.

Диаметры дисков стандартизированы. Нормальный ряд дисков включает в себя следующие значения: 250, 400, 450, 510, 560, 610, 660, 710 и 800 мм. Наиболее употребимыми являются размеры 450, 510 и 660 мм. Большое влияние на технологические свойства диска оказывает угол, характеризующий его сферу (рис. 6.4). Чем больше угол сферы, тем интенсивнее крошится и оборачивается пласт. Для дисковых плугов угол сферы необходим в пределах 31...37°, для лущильников 26...32° и борон 22...26°.

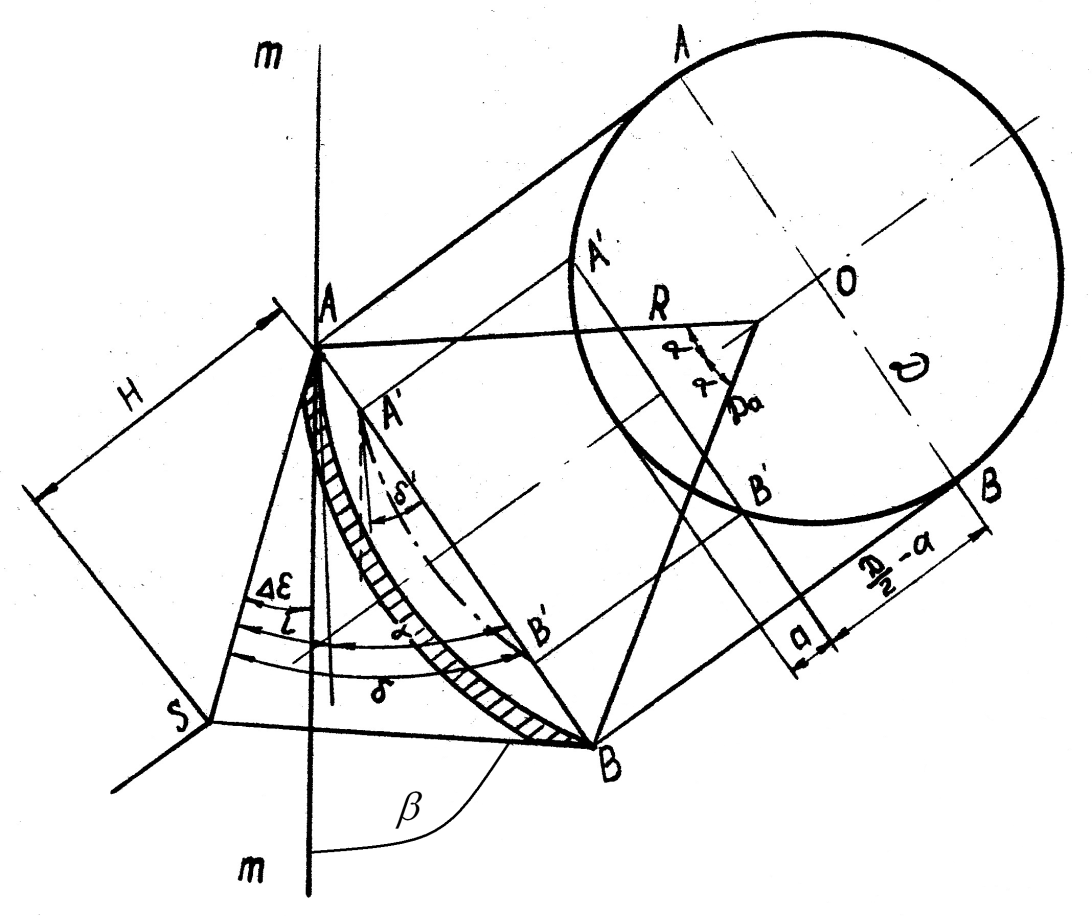
Рис. 6.4. Геометрические параметры сферического диска: α - угол сферы диска; β - угол атаки; δ - угол заточки; δ ¢ - угол заточки на глубине хорды погружения диска; i - угол застрения; Δ ε - затылочный угол на уровне горизонтального диаметра; Δ ε ¢ - затылочный угол на глубине хорды погружения диска; D - диаметр диска; R - радиус сферы диска; D а - длина хорды на глубине обработки почвы; а - глубина обработки почвы

Диаметр диска D и угол сферы α определяют радиус сферы (рис. 6.4):

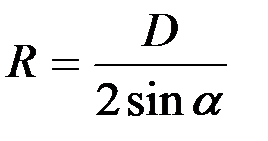. (6.4)

Технологический процесс резания почвы сферическим диском в значительной мере зависит от углов заточки диска δ и заострения i.

Диски затачивают, как правило, с выпуклой, наружной стороны, принимая угол заострения i равным 10...20° у борон и лущильников и 15...25° для плугов.

Так как лезвие диска имеет форму окружности и постоянный угол заострения, то фаска заточки имеет форму усеченного конуса, образующие которого наклонены к плоскости основания под углом заточки δ:

.

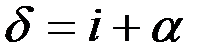Иногда параметром, характеризующим заточку диска, становится высота конуса заточки Н. Величина угла заточки каждого типа дисков, выпускаемых в нашей стране, регламентирована ГОСТом и находится в пределах 37...45°.

Работоспособность дискового орудия во многом определяется величиной затылочного угла Δε. Для качественного резания почвы диском необходимо, чтобы

Δε = 3...5°.

Если это условие выполнить не удается, т.е. Δε ≤ 0, то диск будет деформировать почву широкой фаской заточки, при этом силы сопротивления смятию будут выталкивать диск из почвы.

Для поддержания заданной глубины обработки почвы придется значительно увеличивать массу машины. Тем не менее расчет величины затылочного угла приводит именно к отрицательным значениям. В самом деле, для любой точки лезвия

,

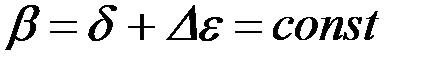тогда

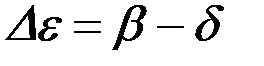. (6.5)

Как ужен было отмечено, максимальное значение угла атаки β равно 35...36°, а минимальный угол заточки диска δ - 37°, тогда Δε = 36° – 37° = – 1°.

И все-таки требование иметь положительный затылочный угол для лущильника выполняется. Дело в том, что величину затылочного угла необходимо определять не на уровне диаметрального сечения диска (как это выполнено на рис. 6.4), а, как говорят, на глубине хорды погружения, т.е. именно там, где диск соприкасается с почвой.

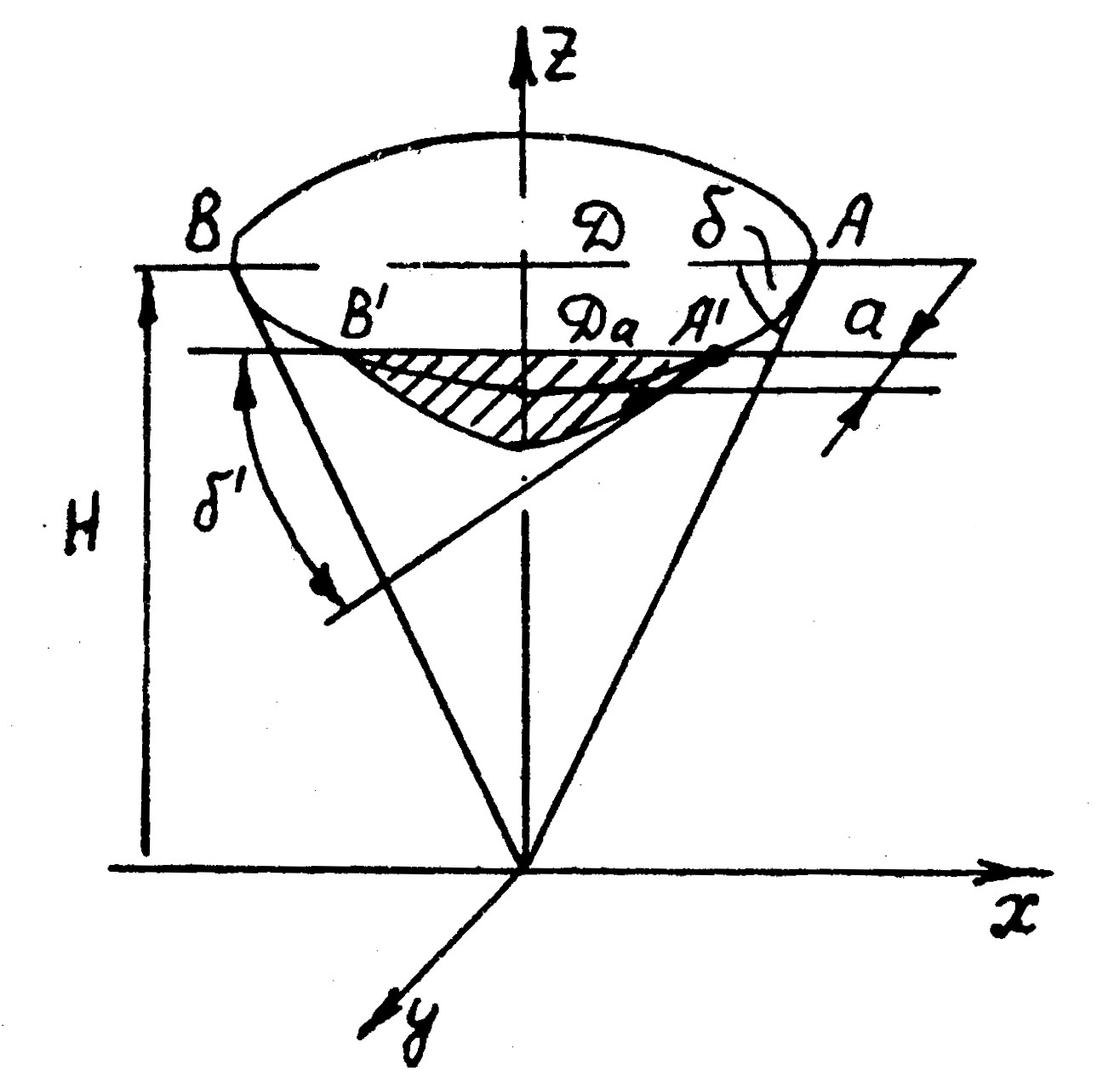
Для того, чтобы проследить за тем, как изменится угол Δε, необходимо проследить за изменением угла δ в разных сечениях конуса, так как по уравнению (6.5) затылочный угол при постоянном для каждого сечения диска значении β зависит именно от δ. Установление связи между значениями углов δ в разных сечениях конуса заточки можно осуществить методами аналитической геометрии. Пусть мы имеем конус высотой Н и диаметром основания D (рис. 6.5). Уравнение круглого конуса, как известно, в декартовых координатах выглядит так:

.

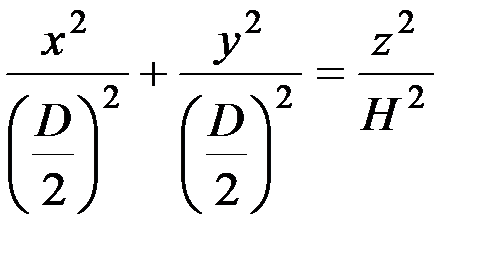Уравнение секущей плоскости, проведенной на расстоянии глубины обработки почвы а от края диска, -

.

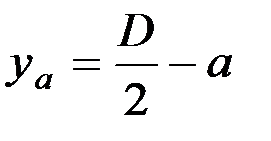В сечении получим гиперболу с уравнением

;

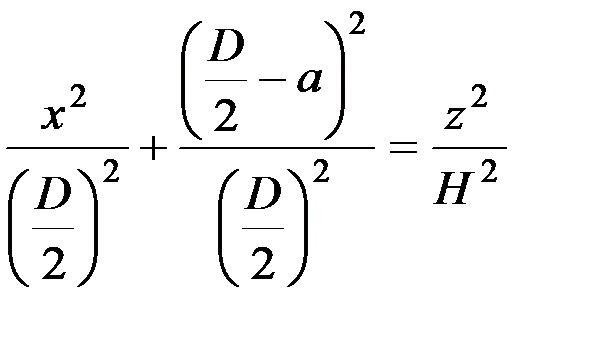или

.

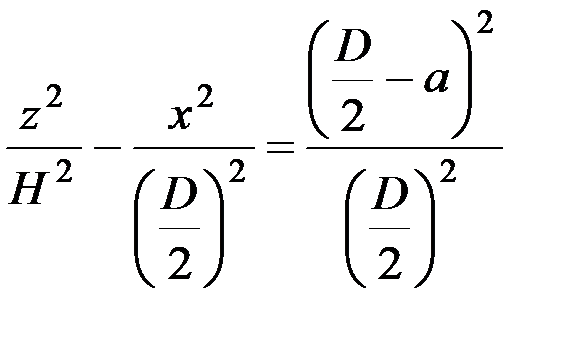Для определения угла наклона касательной к гиперболе необходимо уравнение гиперболы продифференцировать по dx:

.

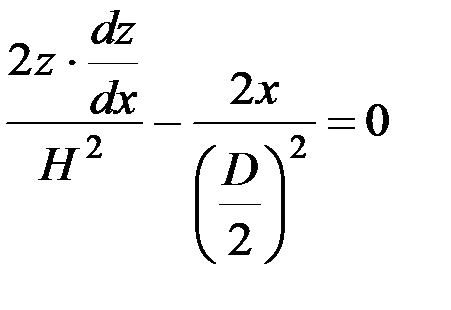Отсюда

.

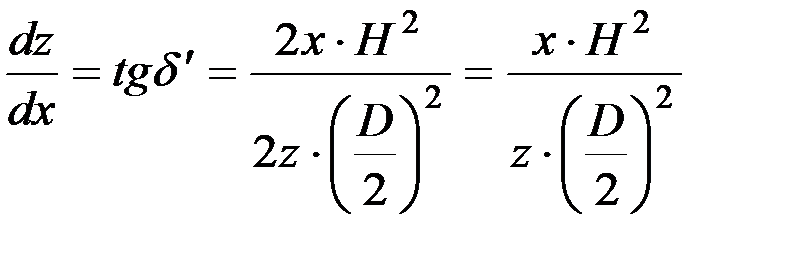Поскольку нас интересует значение δ¢ в точке А¢, то подставим в уравнение координаты точки А¢: ; .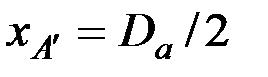

^.

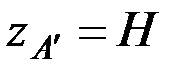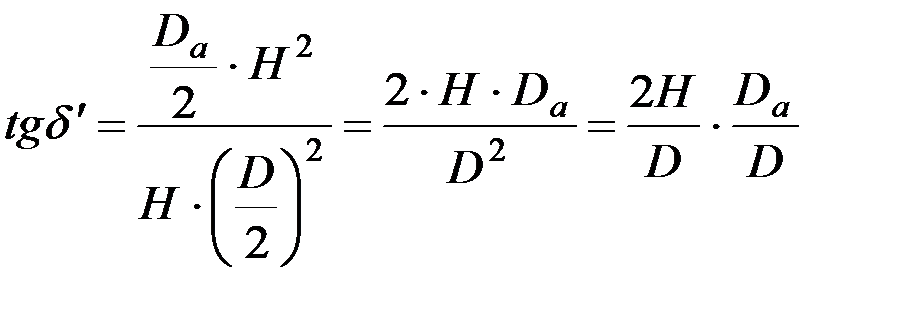Если учесть, что в диаметральном сечении конуса

; ,

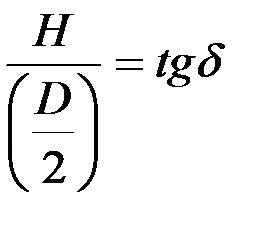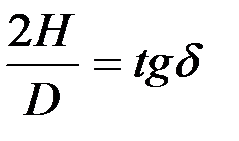окончательно получится

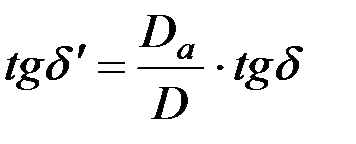. (6.6)

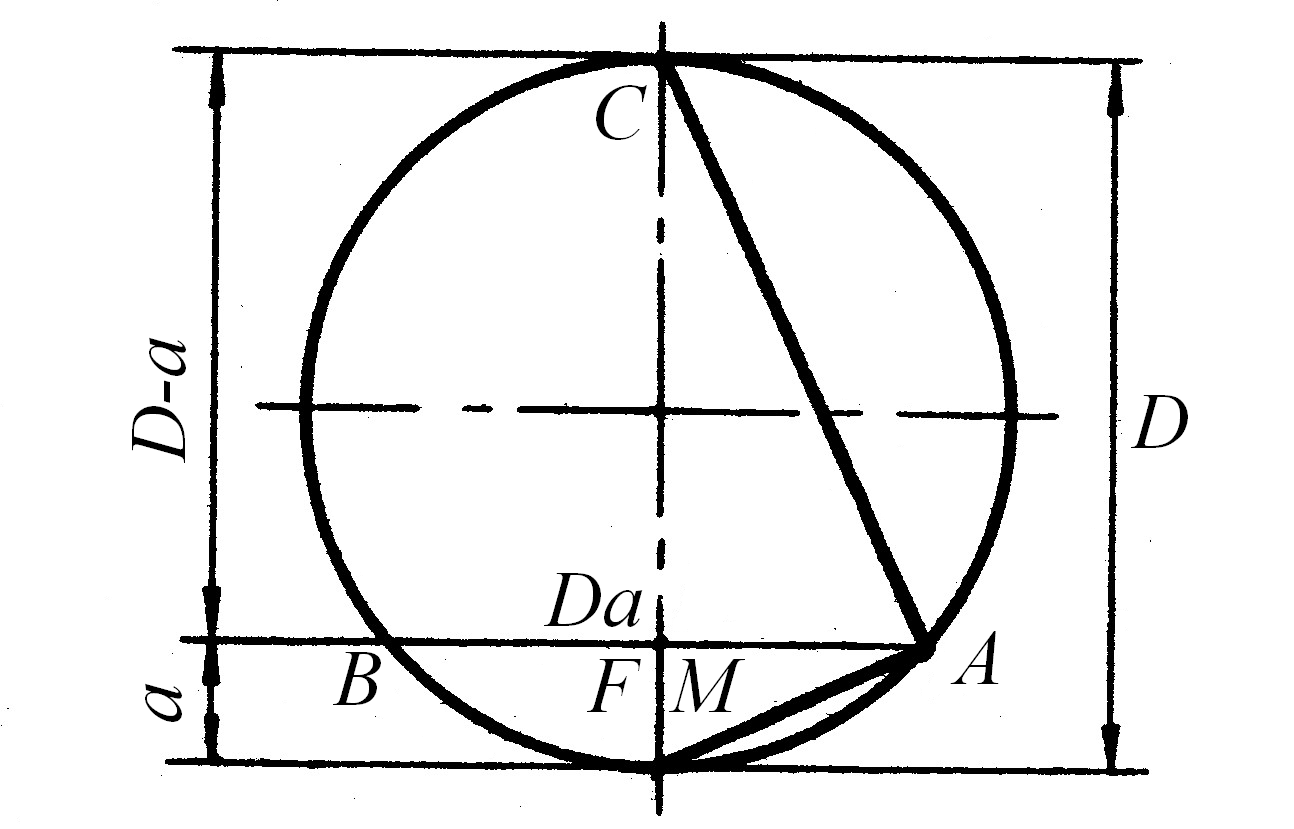
Рис. 6.5. Схема к анализу углов δ в различных сечениях конуса	Рис. 6.6. Определение хорды Da

Поскольку всегда D_a < D, то и угол δ¢ < δ.

Из уравнения 6.5 можно найти теперь величину затылочного угла на глубину хорды погружения:

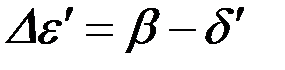. (6.7)

Хорда D_a может быть определена на основе простого геометрического анализа (рис. 6.6).

Треугольники FAM и AMC подобны, так как у них все углы равны ввиду взаимной перпендикулярности сторон. В подобных треугольниках отношение катетов составит

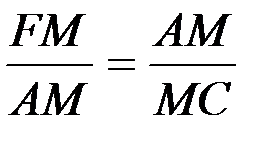; или ,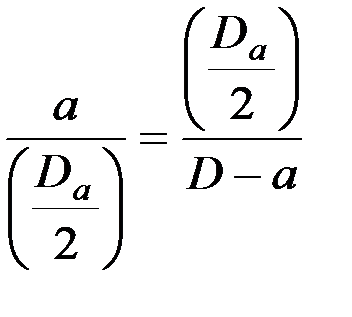

откуда

;

;

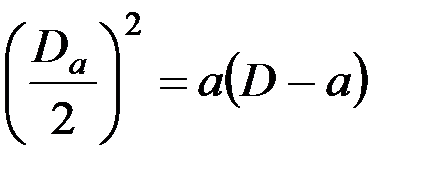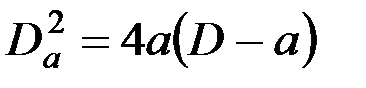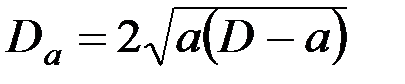. (6.8)

Приведенные геометрические соотношения между параметрами сферического диска позволяют, с одной стороны, определить действительные значения затылочного угла на глубине погружения, а с другой - осуществить определение угла заточки по величине затылочного угла в зоне резания.

Если угол атаки β мал (что характерно для работы дисковых борон), то выполнить условие необходимости положительного угла Δε¢ не удается. В этом случае стремятся обеспечить лишь то, чтобы отрицательный угол Δε¢ был по абсолютной величине не больше i. При таком затылочном угле Δε¢ почва будет сминаться фаской заточки, но тыльная сторона диска деформировать почву не будет.

Дата добавления: 2015-06-04