Уравнение движения удобрений по лопасти диска

Движение частиц по диску определяется прежде всего действием сил на них со стороны лопастей.

В простейшем случае, когда лопасти установлены радиально (рис. 8.3) на частицу, находящуюся на некотором расстоянии х от центра диска действует система сил.

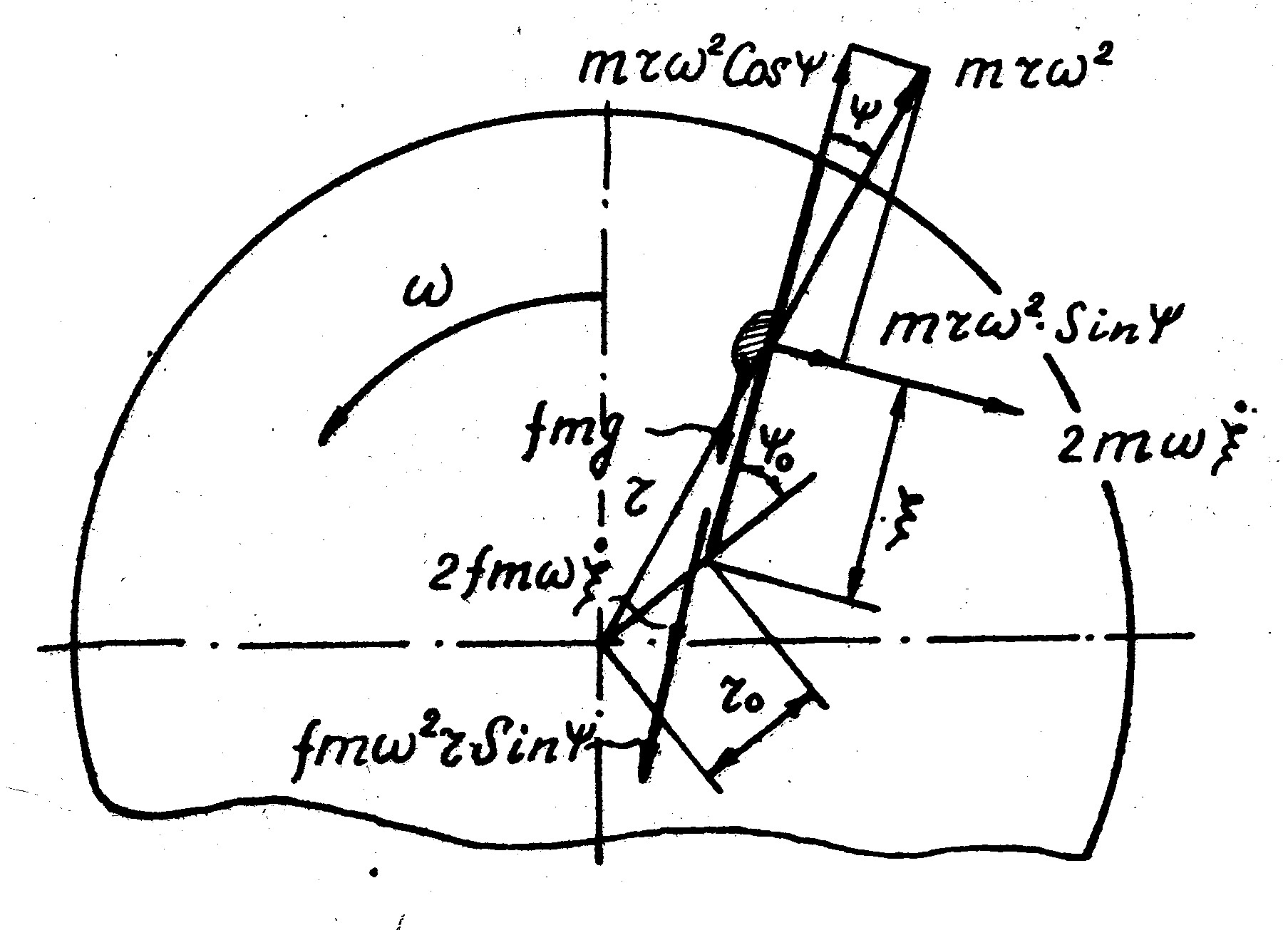
Рис. 8.3. Схема сил, действующих на частицу удобрений, движущуюся вдоль по горизонтальному диску с прямолинейными радиальными лопастями

В наиболее простой, весьма идеализированной модели технологического процесса (когда считается, что удобрения перемещаются как некоторая материальная точка с массой m, т.е. не учитываются сыпучесть среды, пренебрегается влияние возможных колебаний и стохастического характера всех его составляющих) выделяют следующие силы:

- центробежной, ω ² х, действующей вдоль лопасти;

- Кориолисовой, 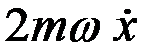, направленной перпендикулярно к лопасти;

- тяжести, mg, прижимающей частицы к горизонтальному диску;

- трения удобрений о диске fmg, где f - коэффициент трения;

- трения удобрений о лопасть .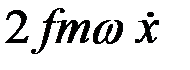

Для составления дифференциального уравнения движения частицы можно воспользоваться принципом Д, Аламбера, т.е. сумму проекций всех сил на направление движения (вдоль лопасти) приравнять силе инерции движущейся массы:

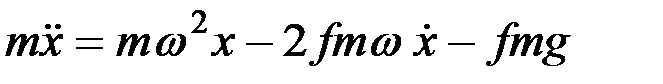; (8.1)

После переноса х и его производных в левую часть уравнения и сокращенных всех членов на m можно получить:

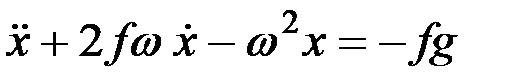, (8.2)

т.е. линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами.

Решение этого дифференциального уравнения, как известно, состоит из общей части и частного интеграла

. (8.3)

Общее решение u зависит от значения корней характеристического уравнения λ.

Для составления характеристического уравнения неизвестную величину заменяют единицей ее производные - соответствующими степенями корней λ, сохраняют все коэффициенты и отбрасывают правую часть.

Применительно к уравнению (8.2) характеристическое уравнение примет вид

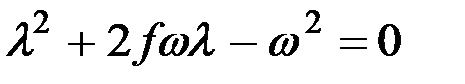. (8.4)

Решением этого квадратного уравнения являются:

,

;

.

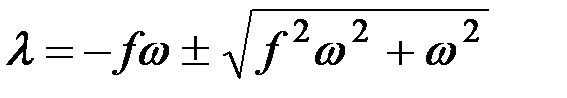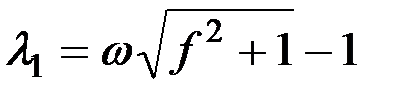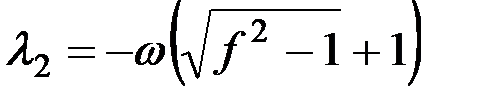Поскольку корни характеристического уравнения оказались действительными числами и отличными друг от друга, то общее решение будет следующим:

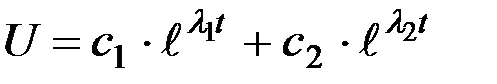, (8.5)

где с₁ и с₂ - постоянные, которые определяют по начальным условиям.

Частный интеграл х₁ зависит от вида правой части.

Если в правой части находится постоянное число, то и частный представит собой тоже постоянное число, допустим А, т.е.

х ₁ = А.

Значение величины А определяют подстановкой в исходное дифференциальное уравнение (8.2)

,

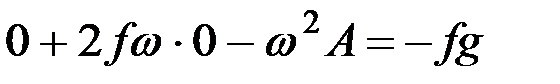откуда

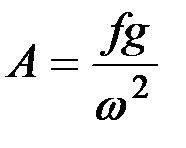. (8.6)

В соответствии с (8.4), (8.5) и (8.6) решением уравнения (8.2) будет:

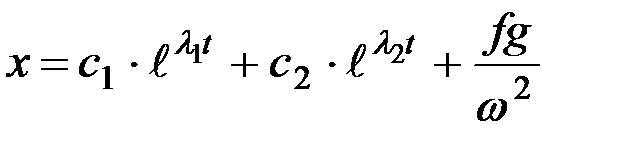. (8.7)

Значения постоянных с₁ и с₂, как уже было отмечено ранее, могут быть определены из начальных условий

При f = 0

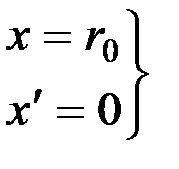. (8.8)

По первому условию уравнение (8.2) примет вид:

,

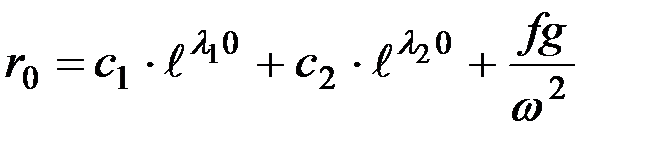откуда

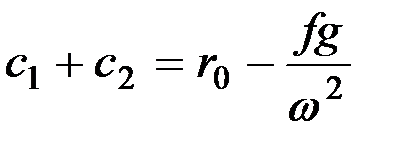. (8.9)

Для использования второго условия (при t = 0, 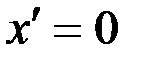) необходимо иметь уравнение скорости перемещения частиц удобрений вдоль по лопасти.

Продифференцировав (8.2) можно найти:

.

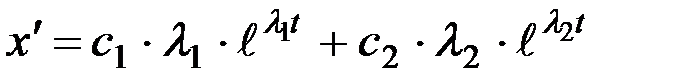После подстановки второго начального условия получается:

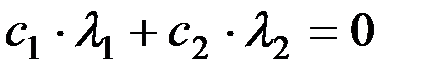. (8.10)

Решением системы уравнений (8.9) и (8.10) находят с₁ и с₂

,

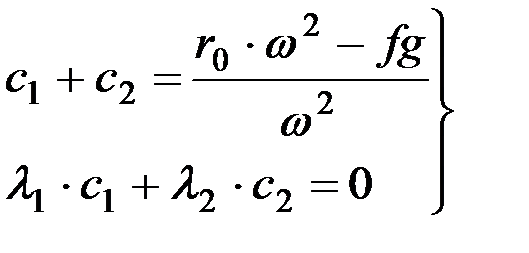
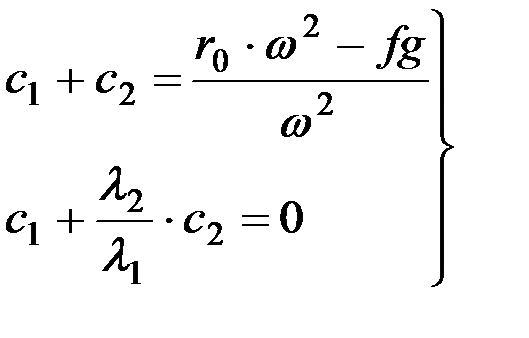
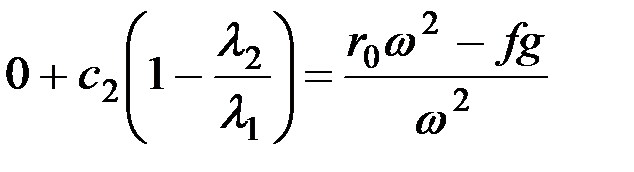или

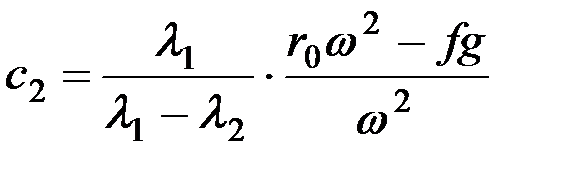. (8.11)

Первая постоянная с₁ окажется равной

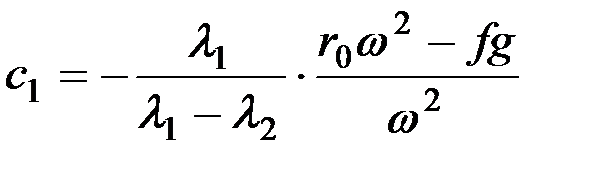. (8.12)

Итак

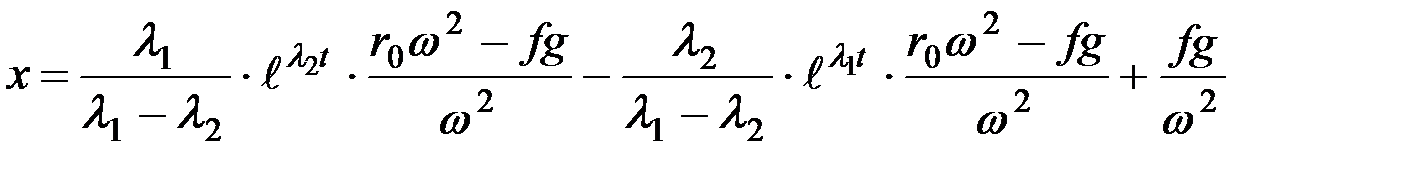
или

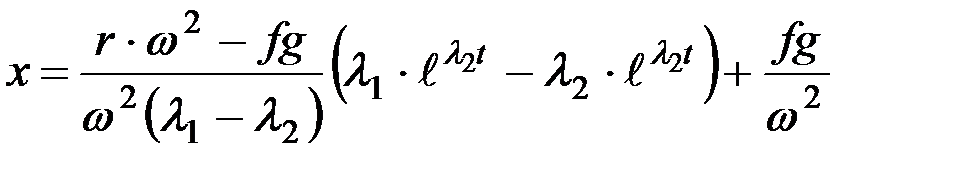. (8.13)

Скорость частиц вдоль лопасти будет равна:

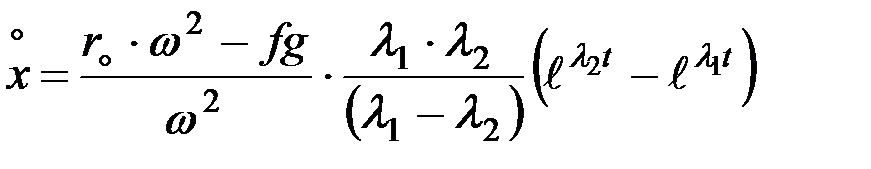. (8.14)

При сходе частиц удобрений с диска координат x=R. После подстановки этого значения в уравнение (8.13) можно получить

,

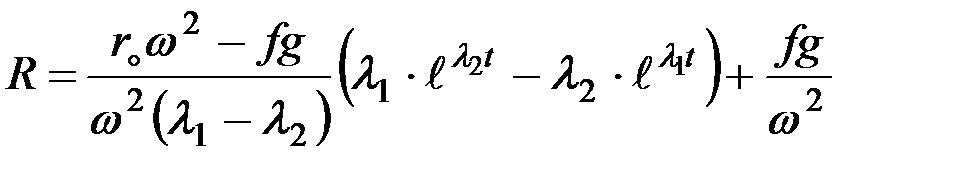или

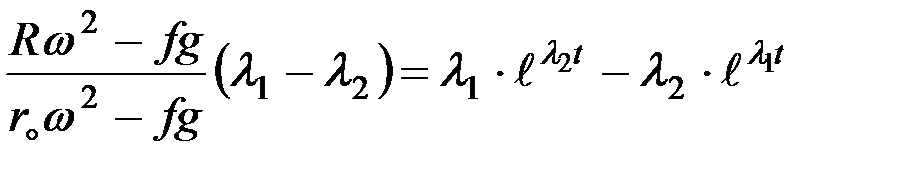. (8.15)

Если это уравнение решить относительно времени t, то можно найти время пребывания удобрения на диске Т (от момента попадания на диск до схода с кромки диска) и после подстановки этого значения в уравнение скорости (8.14) найти V_x (рис. 8.2).

.

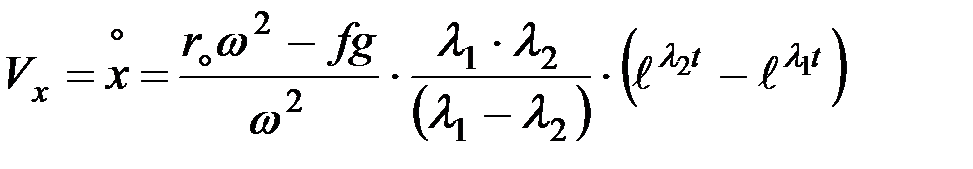Начальная скорость полета частиц после схода их с диска может быть найдена сложением векторов 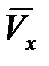и 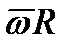(рис. 8.2), например

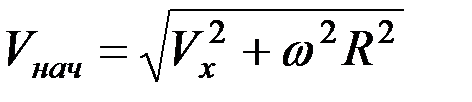. (8.16)

Дата добавления: 2015-06-04