Определение дальности полета удобрений, рассеваемых центробежным диском

На частицу удобрений в момент схода с диска будут действовать сила тяжести и сопротивления воздуха (рис. 8.4).

Сила сопротивления воздуха R_x в диапазоне скоростей 20...30 м/с может быть определена по известной формуле Ньютона:

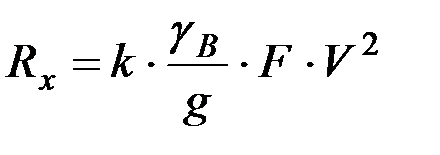, (8.17)

где k - коэффициент сопротивления, зависящий от свойств поверхности частиц;

γ_в - удельный вес воздуха;

F - Миделево сечение (проекция поперечного сечения тела в данный момент на плоскость, перпендикулярную к скорости воздуха);

V - скорость частицы относительно воздуха.

Дифференциальное уравнение полета частиц в направлении оси Х, совпадающей с направлением начальной скорости V_нач, может быть записано как

.

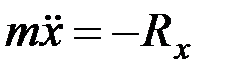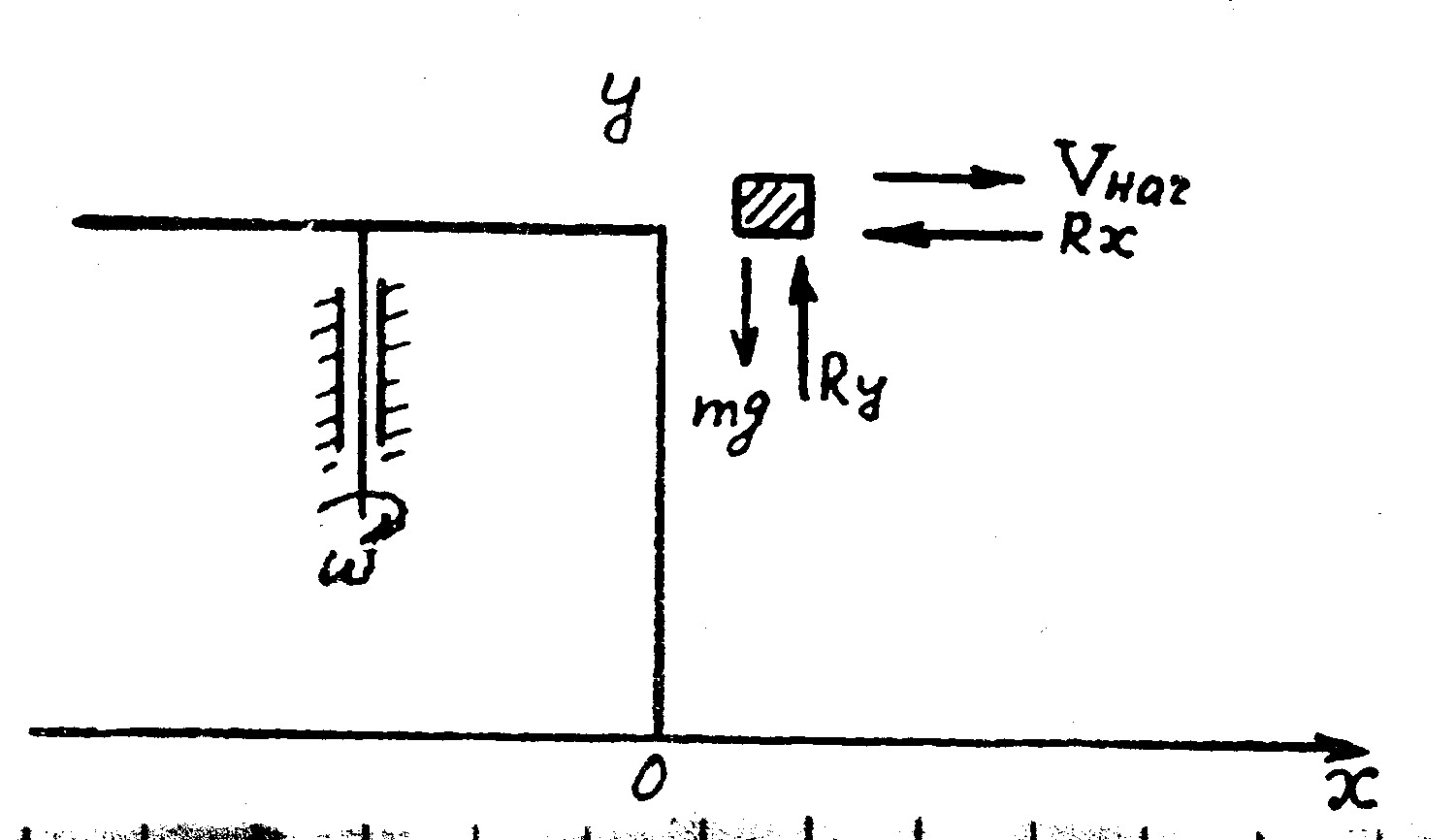
Рис. 8.4. Схема сил, действующих на частицу удобрений после схода с диска

Учитывая значение R_x по уравнению (8.14), получим

.

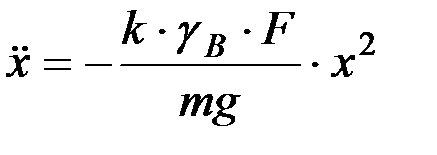Если коэффициенты перед х² обозначить k_n,

,

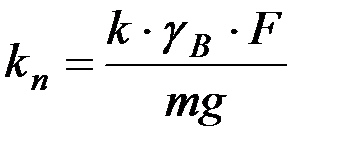то

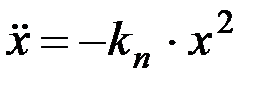, (8.18)

где k_n - коэффициент парусности частиц удобрений.

Решение уравнения (8.18) можно осуществить методом понижения порядка:

, ,

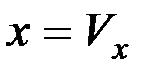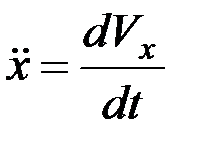тогда

;

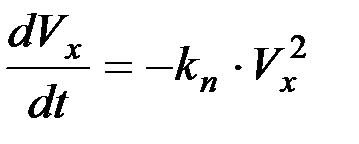или

,

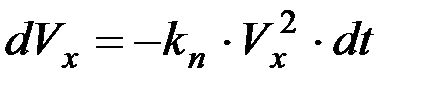но

,

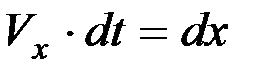тогда

.

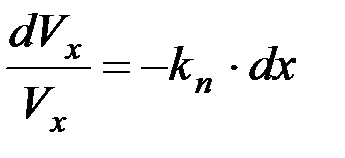Интегрируя уравнение, можно получить

,

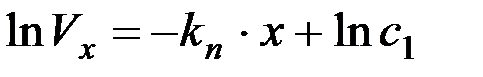или

.

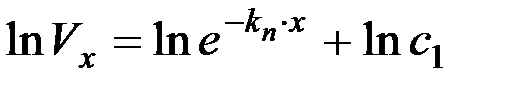Потенцируя это выражение, можно определить

.

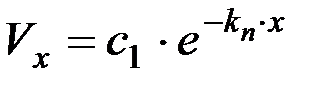Постоянную интегрирования с₁ находят из начальных условий: при х=0 скорость V_x=V_нач.

Таким образом,

.

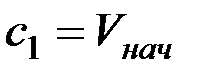Следовательно, уравнение полета частицы будет представлено экспонентой

.

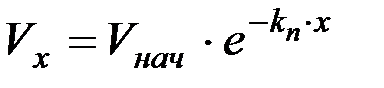Для определения дальности полета ч полученное уравнение нужно проинтегрировать по времени, предварительно вновь разделив переменные

,

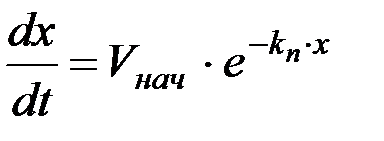или

.

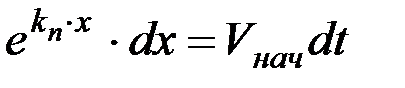Интегралы от правой и левой частей окажутся равными

.

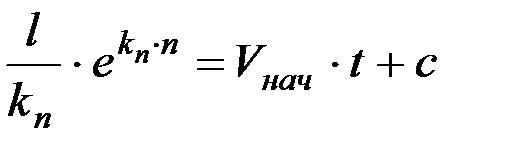Постоянную интегрирования определим из начальных условий при

t = 0; x = 0; ; .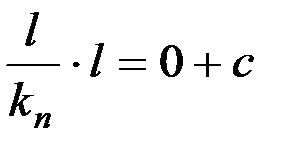

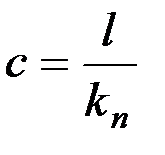С учетом этого

.

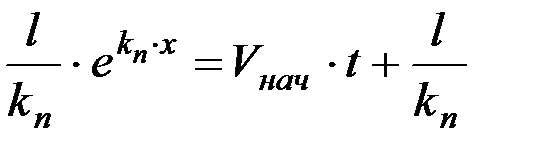Если умножить обе части уравнения, можно получить

.

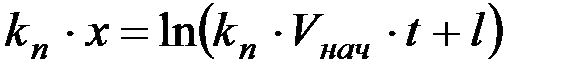Логарифмируя обе части уравнения можно получить

.

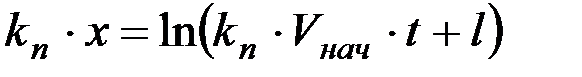Дальность полета частиц в функции времени получит следующий вид:

. (8.19)

Время полета части t может быть найдено по времени падения тела с высоты расположения диска от поверхности почвы Н.

Поскольку скорость движения частиц по вертикали и высота падения небольшие, то сопротивлением воздуха в этом направлении обычно пренебрегают, тогда

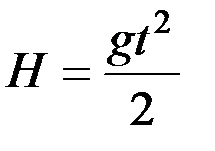, откуда .

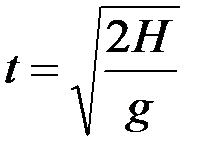Если полученное значение t подставить в уравнение (8.19), то

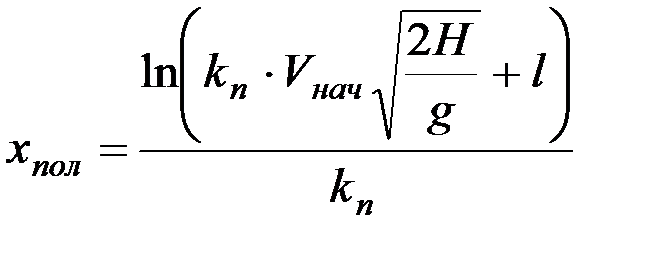. (8.18)

Дальность полета удобрений х_пол определяют одну из важнейших характеристик машины - ширину захвата, которая у большинства разбрасывателей равняется 10...14 м.

Для определения возможностей дальнейшего увеличения ширины захвата разработана компьютерная программа "Центр" (Centr), но уже по более совершенным моделям технологического процесса [1], [2], [3].

В этой программе возможно исследование влияния скорость вращения дисков, диаметр дисков, место подачи удобрений на диск, наклон лопастей вперед или назад, высота установки дисков над почвой, конусность центробежных распределителей, физико-механические свойства удобрений (коэффициенты трения и парусности).

Используя метод вычислительного эксперимента студенты, как правило, находят возможности для увеличения ширины засеваемой полосы до 25...30м, что соответствует лучшим зарубежным и отечественным моделям.

Контрольные вопросы

1. Назовите основные технологически значимые элементы общего устройства центробежного рассеивателя удобрений.

2. Как обеспечивается регулирования нормы внесения удобрений у кузовных разбрасывателей удобрений.

3. Каким образом можно регулировать равномерность распределения удобрений внутри засеваемой полосы.

4. Под действием каких сил находятся частицы удобрений, находящиеся на лопасти центробежного распределителя.

5. Как можно составить дифференциальное уравнение, описывающее движение частиц по лопасти центробежного распределителя?

6. Назовите основные этапы решения дифференциального уравнения движения удобрений по лопасти.

7. Как определить скорость, с которой удобрения сходят с центробежного диска.

8. Что представляет собой дифференциальное уравнение движения удобрений после схода с центробежного диска.

9. Назовите основные этапы решения дифференциального уравнения полета удобрения вплоть до определения дальности полета частиц.

10. Если Вы провели исследование технологического процесса внесения удобрений по компьютерной программе "Центр", то назовите факторы, которые наиболее эффективно увеличивают ширину захвата машины.

11. Назовите конструктивные элементы, позволяющие увеличить ширину захвата центробежного разбрасывателя удобрений.

Литература

1. Кошурников А.Ф. и др. Анализ технологических процессов, выполняемых сельскохозяйственными машинами, с помощью ЭВМ. Пермь, 1995, - 272 с.

2. Кошурников А.Ф. Основы научных исследований в агроинженерии: структура, информация, гипотезы, модели. Пермь изд. ФГБОУ ВПО "Пермская ГСХА", 2012 - 180 с.

3. Турбин Б.Г. Сельскохозяйственные машины. Л.Машиностроение, 1967 г.

Дата добавления: 2015-06-04