Произвольные повороты

Теперь уже понятно, как быть с произвольным поворотом. Во-первых, заметьте, что любая относительная ориентация двух систем координат может быть описана тремя углами (фиг. 4.9).

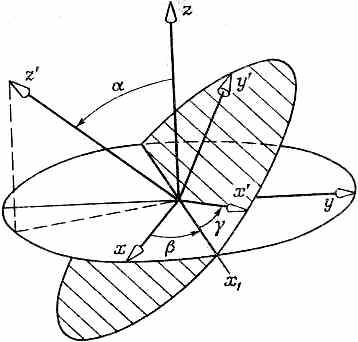
Фиг. 4.9. Ориентацию лю­бой системы координат х', у', г' по отношению к другой системе х, у, z можно опре­делить с помощью углов Эйлера a, b, g.

Если есть система осей х', у', z', ориентированных относительно х, у, z как угодно, то соотношение между ними можно описать тремя углами Эйлера a, b и g, определяющими три последовательных поворота, которые переводят систему х, у, z в систему х', у', z'. Отправляясь от x, у, z, мы повора­чиваем нашу систему на угол bets вокруг оси z, перенося ось х на линию х'. Затем мы проводим поворот на угол а вокруг этой временной оси х ₁, чтобы довести ось z до z'. Наконец, по­ворот вокруг новой оси z (т. е. вокруг z') на угол g переведет ось х ₁в х', а ось у в у'. Мы знаем преобразования для каж­дого из трех поворотов — они даются формулами (4.19) и (4.34). Комбинируя их в нужном порядке, получаем

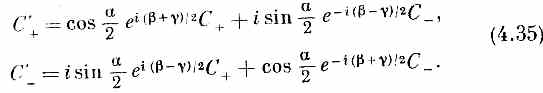
Итак, начав просто с некоторых предположений о свойст­вах пространства, мы вывели преобразование амплитуды при любом повороте. Это означает, что если нам известны ампли­туды того, что любое состояние частицы со спином ¹/₂ перейдет в один из двух пучков прибора Штерна — Герлаха S с осями х, у, z, то мы можем подсчитать, какая часть перейдет в каж­дый пучок в приборе Т с осями х', у' и z'. Иначе говоря, если имеется состояние yчастицы со спином ¹/₂, у которого ам­плитуды пребывания вверху и внизу по отношению к оси z системы координат х, у, z равны С₊=<+|y> и С_-=<-|y>, то тем самым мы знаем амплитуды С₊ и C_- пребывания вверху и внизу по отношению к оси z' любой другой системы х', у", z', Четверка коэффициентов в (4.35) — это члены «матрицы преобразования», с помощью которой можно проецировать амплитуды частицы со спином ¹/₂ в другие системы ко­ординат.

Теперь решим несколько примеров, чтобы посмотреть, как все это работает. Возьмем следующий простой вопрос. Пустим атом со спином ¹/₂ через прибор Штерна — Герлаха, пропу­скающий только состояние (+z). Какова амплитуда того, что атом окажется в состоянии (+ x)? Ось + х — это все равно, что ось +z' системы, повернутой на 90° вокруг оси у. Поэтому в этой задаче проще воспользоваться выражением (4.32), хотя, конечно, можно применить и полное уравнение (4.35). По­скольку С₊ =1 и С_- =0, то получится С'₊ =1/Ö2. Вероятности -это квадраты модулей этих амплитуд; таким образом, 50% шансов за то, что частица пройдет сквозь прибор, отбирающий состояние (+х). Если бы мы поинтересовались состоянием (- х), то амплитуда оказалась бы -1/Ö2, что опять дало бы вероятность ¹/₂, чего и следовало ожидать из симметрии про­странства. Итак, если частица находится в состоянии (+z), то ей в равной степени вероятно побывать в состояниях (+ x) и (- х). Но фазы противоположны.

Ось у тоже без претензий. Частица в состоянии (+ z) имеет равные шансы быть в состоянии (+у) или (- у). Но теперь (согласно формуле для поворота на -90° вокруг оси х) амплитуды суть l/Ö2 и - i /Ö2. В этом случае разница в фа­зах двух амплитуд уже не 180°, как было для (+х)и (- х), а 90°. В этом-то и проявляется различие между х и у.

Вот еще пример. Пусть нам известно, что частица со спином ¹/₂ находится в состоянии y, поляризованном вверх относи­тельно оси А, определяемой углами q и j (фиг. 4.10).

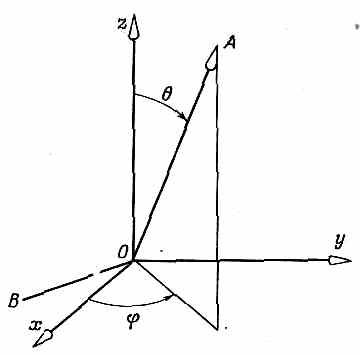
Фиг. 4.10. Ось А, определяе­мая полярными углами q и j.

Мы хо­тим знать амплитуду <C₊|y> того, что частица относительно оси z окажется в состоянии «вверх», и амплитуду <C_-|y> того, что она окажется в состоянии «вниз» относительно той же оси z. Эти амплитуды мы можем найти, вообразив, что А есть ось z' системы, у которой ось х' направлена произвольно, ска­жем лежит в плоскости, образованной А и z. Тогда можно перевести систему А в систему х, у, z тремя поворотами. Во-первых, надо сделать поворот на -p/2 вокруг оси A, что пере­ведет ось x в линию В на рисунке. Затем повернуть на — 0 вокруг линии В (вокруг новой оси х системы А), чтобы ось А попала на ось z. И, наконец, повернуть вокруг оси z на угол (p/2-j).

Вспоминая, что вначале было только одно состояние (+) по отношению к А, получаем

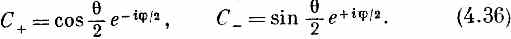
Мы хотели бы напоследок подытожить результаты этой главы в форме, которая окажется полезной для нашей даль­нейшей работы. Во-первых, напомним, что наш основной ре­зультат (4.35) может быть записан в других обозначениях. Заметьте, что (4.35)— это то же самое, что и (4.4) Иначе го­воря, в (4.35) коэффициенты при С₊=<+S|y> и C'_-= <- S |y> суть как раз амплитуды < jT | iS >в (4.4), амплитуды того, что частица в состоянии i по отношению к S окажется в состоя­нии j по отношению к Т (когда ориентация Т по отношению к S дается углами a, b и g). Мы их также называли R^TS_ji в выра­жении (4.6). (Чего-чего, а обозначений у нас хватало!) Например, 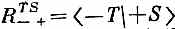— это коэффициент при С₊ в формуле для С_-, а именно i sin(a/2)exp[ i (b-g ) /2]. Поэтому сводку наших ре­зультатов мы можем дать в виде табл. 4.1.

Было бы удобно иметь эти амплитуды расписанными для некоторых особо важных случаев. Пусть R_z(j) — поворот на угол j вокруг оси z. Так же можно обозначить и соответ­ствующую матрицу поворота (опуская молчаливо подразу­меваемые индексы i и j). В том же смысле R_x(j) и R_y(j) будут обозначать повороты на угол j вокруг оси х и оси у,

В табл. 4.2 мы приводим матрицы — таблицы амплитуд < jT | iS >, которые проецируют амплитуды из системы S в систему Т, где Т получается из S указанным поворотом.

* Нетрудно показать, что систему х, у, z можно перевести в систему х', у', z' следующими тремя поворотами вокруг первоначальных осей: 1) повернуть на угол g вокруг первоначальной оси z; 2) повернуть на угол а вокруг первоначальной оси х; 3) повернуть на угол b вокруг первоначальной оси z.

Дата добавления: 2015-06-04