Преобразование к повернутой системе координат

Рассмотрим опять «усовершенствованный» прибор Штерна— Герлаха, описанный в предыдущей главе. Пучок частиц со спи­ном ¹/₂, входящих слева, расщепляется, вообще говоря, на два пучка, как показано схематически на фиг. 4.1.

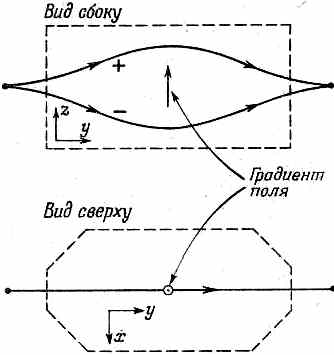
Фиг. 4.1. «Усовершенствованный» прибор Штерна — Герлаха с пучками частиц со спином ¹/₂.

(При спине 1 пучков было три.) Как и раньше, пучки в конце снова сводятся в одно место, если только один из них не будет перекрыт «перегородкой», которая перехватит его на полпути. На рисунке имеется стрелка, которая показывает направление роста величины поля, скажем положение магнитного полюса с острым наконечником. Эта стрелка пусть будет представлять собой на правление вверх для данного прибора. В каждом аппарате ее положение фиксировано, что позволяет указывать взаимную ориентацию нескольких приборов относительно друг друга. Наконец, предположим еще, что направление магнитного поля относительно стрелки во всех магнитах одинаково.

Будем говорить, что атомы из «верхнего» пучка находятся по отношению к этому прибору в состоянии (+), атомы из «нижнeгo» — в состоянии (-). (Нуль-состояния для спина ¹/₂ не

существует.)

Положим теперь, что мы поставили два наших усовершен­ствованных прибора Штерна — Герлаха один за другим фиг. 4.2, а).

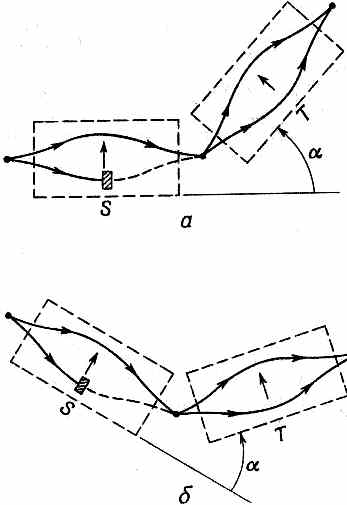
Фиг. 4.2. Два эквивалентных эксперимента.

Первый (назовем его S) можно употребить на то, что­бы приготовлять чистое состояние (+ S) или (- S), загораживая то один, то другой пучок. [На рисунке приготовляется чистое состояние (+ S).] При любом расположении всегда есть неко­торая амплитуда того, что частица, выходящая из S, окажется в пучке (+Т) или (- Т) второго прибора. Всего таких ампли­туд четыре: амплитуды перехода от (+ S) к (+ T), от (+S) к (-Т), от (-S) к (+Т) и от (- S) к (- T). Эти амплитуды — просто четыре коэффициента матрицы преобразования R _ji перехода от представления S к представлению Т. Можно счи­тать, что первый прибор «приготовляет» определенное состояние в одном представлении, а второй «анализирует» это состояние в терминах второго представления. Мы хотим научиться отве­чать на такие вопросы: если, загородив один из пучков в S, мы приготовили атом в данном состоянии, например в состоянии (+5), то каково будет изменение, которое он испытает, пройдя через прибор Т, который настроен на состояние (- T)? Резуль­тат, конечно, будет зависеть от углов между системами S и Т.

Мы должны объяснить, почему есть надежда найти коэф­фициенты R_ji теоретически. Почти невозможно поверить, что если у частиц спин был выстроен в направлении +z, то есть хоть какой-то шанс обнаружить, что ее спин ориентирован в направлении + x или в каком-либо другом направлении. Это дей­ствительно почти невозможно. Но все же не совсем. Это на­столько невозможно, что остается лишь один путь, каким это происходит, а если этот путь один, то его уже можно найти.

Первое рассуждение можно провести так. Предположим, что, как показано на фиг. 4.2, а, прибор Т направлен вверх под уг­лом а относительно S. Пусть через S проходит только пучок (+), а через Т — только пучок (-). Мы измерили некоторую вероятность того, что частицы, выходя из S, пройдут сквозь Т. Теперь предположим, что мы делаем второе измерение при­бором, показанным на фиг. 4.2, б. Относительная ориентация S и Т одинакова, но вся система расположена в пространстве под другим углом. Мы хотим предположить, что оба опыта приведут к одному и тому же значению вероятности того, что частица в чистом состоянии относительно S окажется в некото­ром определенном состоянии относительно Т, Иными словами, мы предполагаем, что результат любого опыта такого рода оди­наков, что сама физика одинакова, как бы весь прибор ни был ориентирован в пространстве. (Вы скажете: «Это самоочевидно». Но это все же только предположение, и оно «правильно» только тогда, если так действительно бывает.) Это означает, что коэффициенты R_ji зависят лишь от взаимного расположения S и Т в пространстве, а не от абсолютного их расположения. Выражаясь иначе, R_ji зависит только от поворота, который переводит S в Т, потому что общим для фиг. 4.2, а и б, очевидно, является трехмерный поворот, переводящий прибор S в положе­ние прибора Т. Когда матрица преобразования R_ji зави­сит, как в нашем случае, только от поворота, ее называют матрицей поворота.

Для следующего шага нужно еще немного информации. Пусть мы добавили третий прибор (назовем его U), стоящий вслед за Т под каким-то произвольным углом (фиг. 4.3, а).

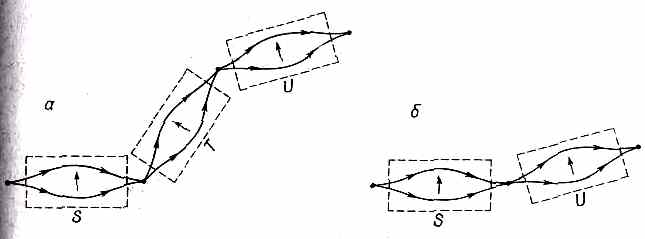
Фиг. 4.3. Если Т «открыт до отказа», то б эквивалентно а.

(Все это начинает выглядеть устрашающе, но в этом-то и прелесть отвлеченного мышления: самые сверхъестественные опыты можно ставить, просто проводя новые линии!) Что же пред­ставляет собой преобразование S ® Т ® U? Фактически нас интересует амплитуда перехода из некоторого состояния по отношению к S к некоторому другому состоянию по отношению к U, если известны преобразования от S к Т и от Т к U, Поин­тересуемся сперва опытом, в котором в Т открыты оба канала. Ответ можно получить, дважды подряд применяя (4.5). Для перехода от S -представления к T -представлению имеем

где верхние индексы TS нужны, чтобы отличать это R от R^UT, когда мы будем переходить от Т к U.

Обозначая амплитуды появления атома в базисных состоя­ниях представления U через C"_k, можно связать их с T -амплитудами, применяя (4.5) еще раз; получим

Теперь можно из (4.6) и (4.7) получить преобразование от S прямо к U. Подставляя С'_j из (4.6) в (4.7), имеем

Или, поскольку в R^UT_kj отсутствует i, можно поставить сум­мирование по i впереди и написать

Это и есть формула двойного преобразования.

Заметьте, однако, что, пока пучки в Т не загораживаются, состояния на выходе из Т те же, что и при входе в него. Мы могли бы с равным успехом делать преобразования из S -представления прямо в представление U. Это значило бы, что прибор U по­ставлен прямо за S, как на фиг. 4.3, б. В этом случае мы бы написали

где R^US_ki — коэффициенты, принадлежащие этому преобразо­ванию. Но ясно, что (4.9) и (4.10) должны приводить к одинако­вым амплитудам С"_k, причем независимо от того, каково было то начальное состояние j, которое снабдило нас амплитудами С _i. Значит, должно быть

Иными словами, для любого поворота S®U базиса, если рас­сматривать его как два последовательных поворота S®Т и Т®U, можно получить матрицу поворота r^us_ki из матриц двух частных поворотов при помощи формулы (4.11). Если угод­но, (4.11) следует прямо из (4.1) и представляет собой лишь другую запись формулы:

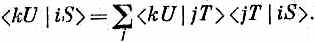
Для полноты добавим еще следующее. Но не думайте, что это будет что-то страшно важное; если хотите, переходите, не читая, прямо к следующему параграфу. Надо сознаться, что то, что мы сказали, не совсем верно. Мы не можем на самом деле утверждать, что (4.9) и (4.10) обязаны привести к абсолют­но одинаковым амплитудам. Одинаковыми должны оказаться только физические результаты; сами же амплитуды, могут отличаться на общий фазовый множитель типа e ^id, не меняя результатов никаких расчетов, касающихся реального мира. Иначе говоря, вместо (4.11) единственное, что можно утвер­ждать,— это

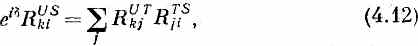
где d — какая-то вещественная постоянная величина. Смысл этого добавочного множителя е ^id, конечно, в том, что амплиту­ды, которые мы получим, пользуясь матрицей R^US, могут все отличаться на одну и ту же фазу (е^-id) от амплитуд, которые получились бы из двух поворотов R^UT и R^TS. Но мы знаем, что если все амплитуды изменить на одинаковую фазу, то это ни на чем не скажется. Так что при желании можно этот фазовый множитель просто игнорировать. Оказывается, однако, что если определить нашу матрицу поворота особым образом, то этот фазовый множитель вообще не появится: б в (4.12) всегда будет нулем. Хотя это и не отражается на наших дальнейших рассуждениях, мы беремся это быстро доказать, пользуясь ма­тематической теоремой о детерминантах. [А если вы до сих пор мало знакомы с детерминантами, то не следите за доказатель­ством и прямо переходите к определению (4.15).)

Во-первых, следует напомнить, что (4.11) — это математи­ческое определение «произведения» двух матриц. (Просто очень удобно говорить «R^US есть произведение R^UT и R^TS».) Во-вторых, существует математическая теорема (которую для используемых здесь матриц 2X2 вы легко докажете), утверждающая, что детерминант «произведения» двух матриц есть произведение их детерминантов. Применив эту теорему к (4.12), получим

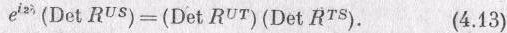
(Мы отбрасываем нижние индексы, они здесь ничего полезного нам не сообщают.) Да, слева стоит 2S! Вспомните, что мы имеем дело с матрицами 2x2; каждый член в матрице R^US_ki умножен на е^id, а каждый член в детерминанте (состоящий из двух мно­жителей) получается умножением на е^i2d. Извлечем из (4.13) корень и разделим на него (4.12):

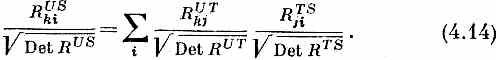
Добавочный фазовый множитель исчез.

Дальше оказывается, что если мы хотим, чтобы все наши амплитуды в любом заданном представлении были нормированы (а это, как вы помните, означает, что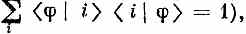

то у всех матриц поворота детерминанты окажутся чисто мни­мыми экспонентами, наподобие е^ia. (Мы не будем этого дока­зывать; вы сами потом увидите, что это всегда так.) Значит, мы сможем, если захотим, выбрать все наши матрицы поворота R так, чтобы фаза их получалась однозначно, взяв Det R =1. Это будет делаться так. Пусть мы каким-то произвольным об­разом определили матрицу поворота R. Возьмем за правило «приводить» ее к «стандартной форме», определяя

Для получения однозначных фаз мы просто умножаем каждый член в R на один и тот же фазовый множитель. В дальнейшем мы будем всегда предполагать, что наши матрицы были приве­дены к «стандартной форме»; тогда мы сможем пользоваться прямо формулой (4.11) без каких-либо добавочных фазовых множителей.

Дата добавления: 2015-06-04