
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Архимеда
|
|
|
|
Физические понятия как основа решения геометрических задач
Интересным в этом плане является знакомство с применением физических понятий к решению геометрических задач.
Подобный путь решения чисто математических проблем имел место на протяжении всей истории развития науки математики. Ещё до нашей эры великий древнегреческий мыслитель Архимед обнаружил возможность доказывать новые математические факты "механическим" методом с использованием принципа рычага. В частности, этим способом им была установлена теорема о том, что: Три медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1. При доказательстве используются следующие вопросы:
материальная точка;
центр масс двух материальных точек:
центр масс системы материальных точек;
свойства центра масс;
теорема Архимеда о медианах треугольника.
Три медианы тpeугольника имеют общую точку, и каждая из медиан делится этой точкой в отношении 2: 1, считая от вершины.
Доказательство (предложенное Архимедом).
Пусть AВC - данный треугольник. AM, CP, ВК - его медианы (рис.11). Поместим в вершины треугольника равные массы, например, по 1грамму. Получившаяся система трёх материальных точек 1A, 1В, 1С имеет однозначно определённый центр масс в некоторой точке О (существование и единственности центра масс). В силу свойства о перегруппировке центров масс положение центра масс не изменится, если массы материальных точек 1B и 1С перенести в их центр масс, то есть, согласно правилу рычага, в точку М. Но тогда точка О окажется центром масс лишь двух материальных точек 2М и 1А. Значит. О 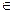 [АМ]. Аналогично убеждаемся в том. что О
[АМ]. Аналогично убеждаемся в том. что О 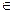 [ВК] и O
[ВК] и O 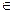 [CP]. Таким образом все медианы имеют общую точку О. Кроме того, по правилу рычага имеем 2
[CP]. Таким образом все медианы имеют общую точку О. Кроме того, по правилу рычага имеем 2 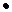 ОМ=1
ОМ=1  ОА, или OA:ОМ = 2:1. Теорема доказана.
ОА, или OA:ОМ = 2:1. Теорема доказана.
Разумеется, для того, чтобы получать математически строгие решения геометрических задач, все сформулированные положения, апеллирующие к понятиям механики, должны быть математически обоснованы.
Пример 1. Сила 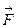 = {1; 3; 2} приложена в точке В (3; 4; 5). Найти момент силы
= {1; 3; 2} приложена в точке В (3; 4; 5). Найти момент силы 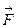 относительно точки А (1; 2; 3).
относительно точки А (1; 2; 3).
Пример 2. Момент сил, действующих на диполь. Момент сил, действующих на диполь (рис. 1.16, б) в однородном внешнем электрическом поле, определяется в физике, электротехнике с помощью векторного произведения следующим образом:
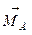 =
= 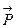
 , |
, | 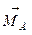 | = |
| = | 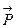 ||
||  |sin
|sin 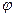 ,
,
 где
где 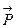 = q
= q  — вектор электрического момента диполя, вектор
— вектор электрического момента диполя, вектор  =
= 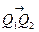 направлен от отрицательного к положительному заряду диполя,
направлен от отрицательного к положительному заряду диполя,  — вектор напряженности электрического поля. Этот момент можно записать и иначе, в соответствии с его механическим смыслом, как момент пары сил
— вектор напряженности электрического поля. Этот момент можно записать и иначе, в соответствии с его механическим смыслом, как момент пары сил 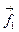 и
и 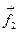 взаимодействия точечных зарядов q
взаимодействия точечных зарядов q 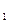 и q
и q 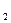 с внешним электрическим полем
с внешним электрическим полем 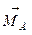 =
= 
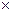
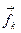 , где к = 1,2.
, где к = 1,2.
Вектор  направлен к точке приложения силы
направлен к точке приложения силы 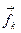 = q
= q 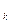
 , где q
, где q 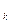 — заряд со своим знаком.
— заряд со своим знаком.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 2223; Нарушение авторских прав?; Мы поможем в написании вашей работы!