
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формулы Определение
|
|
|
|
· ½ x ½ ³ 0
· ½ x - y ½ ³ ½ x ½ - ½ y ½ 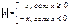
· ½- x ½=½ x ½
· ½ x × y ½ = ½ x ½ × ½ y ½
· ½ x ½ ³ x
· ½ x: y ½ =½ x ½: ½ y ½
· ½ x + y ½ £ ½ x ½ + ½ y ½
½ x ½2 = x 2
Неравенства
Определения:
Неравенством называется выражение вида:
a < b (a £ b), a > b (a ³ b)
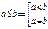
Основные свойства:
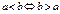
| 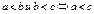
|
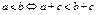
| 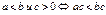
|
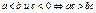
| 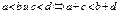
|
Модуль: уравнения и неравенства
1. 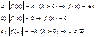
2. 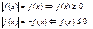
3. 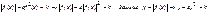
4. 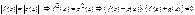
5. 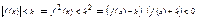
Периодическая дробь
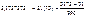 Правило:
Правило: 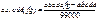
Признаки делимости чисел:
Проценты
Определение:
Процентом называется сотая часть от числа. 1%A = 0,01A
Основные типы задач на проценты:
Сколько процентов составляет число A от числа B? 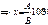
B - 100%
A - x%
Сложные проценты.
Число A увеличилось на 20%, а затем полученное число уменьшили на 25%.
Как, в итоге, изменилось исходное число?
1) A1 = (100% + 20%)A = 120%A = 1,2A
2) A2 = (100% - 25%)A1=75%A1 = 0,75A1 = 0,75×1,2A = 0,9A = 90%A
3) A1 – A = 90%A – 100%A = -10%A
Þ Ответ: уменьшилось на 10%. Изменение величины.
Как изменится время, если скорость движения увеличится на 25%?
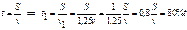
Þ Ответ: уменьшится на 20%
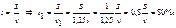
Þ Ответ: уменьшится на 20%
Среднее арифметическое, геометрическое
Среднее арифметическое: 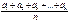
Среднее геометрическое: 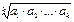
Уравнение движения
Пусть 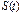 - уравнение движения материальной точки, где S – путь, t – время движения.
- уравнение движения материальной точки, где S – путь, t – время движения.
Тогда: 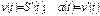 ,
,
где 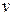 – скорость,
– скорость, 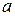 - ускорение.
- ускорение.
Определенный интеграл

Первообразная элементарных функций
| № | f(x) | F(x) | № | f(x) | F(x) | ||
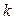
| 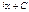
| 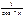
| 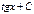
| ||||
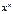
| 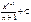
| ||||||
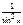
| 
| ||||||
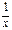
| 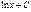
| ||||||
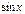
| 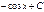
| 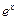
| 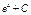
| ||||
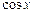
| 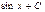
| 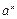
| 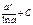
|
Правила вычисления первообразной функции
Определение: Функция F(x) называется первообразной для функции f(x), если 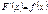 .
.
| Функция | Первообразная |
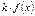
| 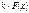
|
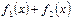
| 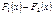
|
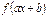
| 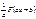
|
Правила вычисления производной функции
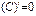
| 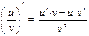
|
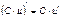
| |
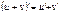
|  Сложная функция: Сложная функция:
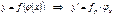
|
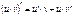
|
Производные элементарных функций
| № | Функция | Производная | № | Функция | Производная | ||
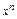
| 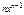
| 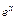
| 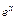
| ||||
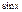
| 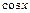
| 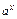
| 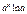
| ||||
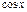
| 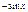
| ||||||
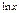
| 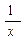
| ||||||
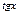
| 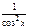
| ||||||
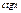
| 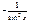
| 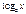
| 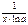
|
Равносильные уравнения:
| Исходное уравнение | Равносильное уравнение (система) | |
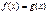
| Û | 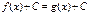
|
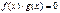
| Û | 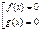
|
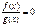
| Û | 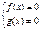
|
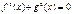
| Û | 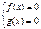
|
Числовые множества:
| Натуральные числа | N = { 1; 2; 3; 4;..} |
| Целые числа | Z = N È { 0; -1; -2; -3; …} |
| Рациональные числа | Q = Z È 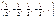
|
| Действительные числа | R = Q È 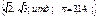
|
Тригонометрия
Основные триг. формулы
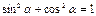 Þ
Þ 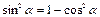
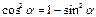
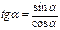
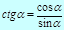 Þ
Þ 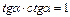
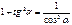
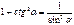
Формулы суммы функций
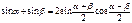
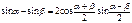
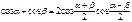
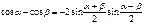
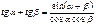
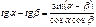
Формулы суммы аргументов:
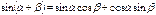
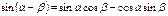
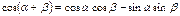
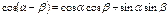
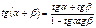
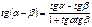
Формулы произведения функций
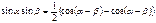
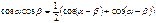
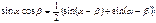
Формулы половинного аргумента
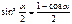
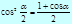
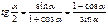
Формулы двойного аргумента
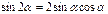
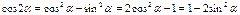
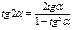
Формула дополнительного угла
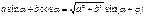 где
где
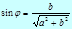

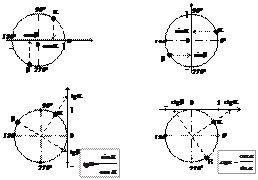 Определение тригонометрических функций
Определение тригонометрических функций
Универсальная подстановка
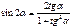
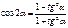
Свойства тригонометрических функций
| Функция | Свойства | |||
| Область определения | Множество значений | Четность-нечетность | Период | |
| cosx | 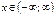
| 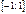
| cos(-x)= cosx | 2p |
| sinx | 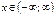
| 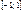
| sin(-x)= -sinx | 2p |
| tgx | 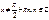
| 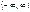
| tg(-x)= -tgx | p |
| ctgx | 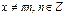
| 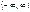
| ctg(-x)= -ctgx | p |
Тригонометрические уравнения
Косинус:
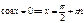
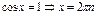
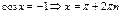
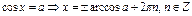
Уравнения с синусом
Частные формулы:

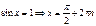
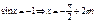
Общая формула:
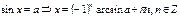
Уравнения с тангенсом и котангенсом
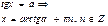
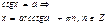
Формулы обратных триг функций
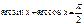
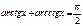
| Если 0 < x £ 1, то arccos(-x) = p - arccosx arcsin(-x) = - arcsinx | Если x > 0, то arctg(-x) = - arctgx arcctg(-x) = p - arcctgx |
Обратные триг функции
| Функция | Свойства | ||
| Область определения | Множество значений | ||
| arccosx | 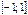
| [ 0; p ] | |
| arcsinx | 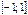
| [-p/2; p/2] | |
| arctgx | 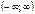
| (-p/2; p/2) | |
| arcctgx | 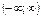
| (0; p) | |
Геометрия
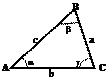 Теорема косинусов, синусов
Теорема косинусов, синусов
Теорема косинусов:
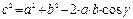
Теорема синусов:
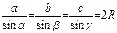
Площадь треугольника
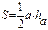
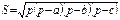
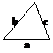 | 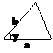 | ||||
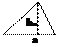 |

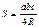
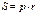
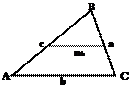 Средняя линия
Средняя линия
Средняя линия – отрезок, с соединяющий середины двух с сторон треугольника.
Средняя линия параллельна т третьей стороне и равна е её половине: 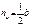
Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного
Равносторонний треугольник
треугольник, у которого все стороны равны.
v Все углы равны 600.
v Каждая из высот является одновременно биссектрисой и медианой.
v Центры описанной и вписанной окружностей совпадают.
v Радиусы окружностей: 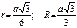
Площадь 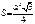
Равнобедренный треугольник
треугольник, у которого две стороны равны.
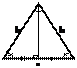 1.Углы, при основании треугольника, равны
1.Углы, при основании треугольника, равны
2.Высота, проведенная из вершины, является б биссектрисой и медиан
|
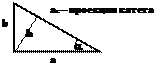 |
v Теорема Пифагора: 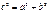 Площадь:
Площадь: 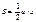
v Тригонометрические соотношения: 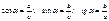
v Центр описанной окружности лежит на середине гипотенузы.
v Радиусы окружностей: 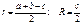
v Высота, опущенная на гипотенузу: 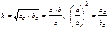
v Катеты: 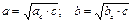
Основные соотношения в треугольнике
Ø Неравенство треугольника:
a + b > c; a + c > b; b + c > a
Ø Сумма углов: a + b + g = 1800
Ø Против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.
Ø 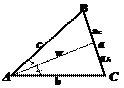 Против равных сторон лежат равные углы, и обратно, против равных углов лежат равные стороны.
Против равных сторон лежат равные углы, и обратно, против равных углов лежат равные стороны.
Биссектриса
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
· Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам: ab: ac = b: c
· Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
· 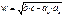

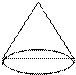 Конус
Конус

|
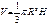
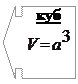
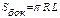
|
 |
Усеченный конус
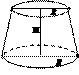 |
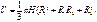
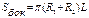
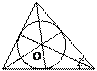 |
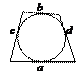 Вписанная окружность
Вписанная окружность
· Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
· Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой:
a + b = c + d
Описанная окружность
Касательная, секущая 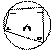

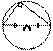
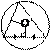
·
· Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.
· Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
· Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
· Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой: 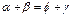
Длина окружности, площадь
 |

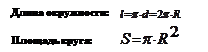
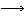 |
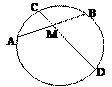 Хорда
Хорда
Хорда – отрезок, соединяющий две точки окружности.
· Диаметр, делящий хорду пополам, перпендикулярен хорде.
· В окружности равные хорды равноудалены от центра окружности.
· Отрезки пересекающихся хорд связаны равенством:
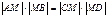
Шар
 |
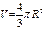
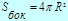
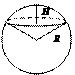 |
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 516; Нарушение авторских прав?; Мы поможем в написании вашей работы!