Электрон в трехмерной решетке

Еще немного о том, как можно применить те же идеи, чтобы понять, что происходит с электроном в трех измерениях. Резуль­таты оказываются очень похожими. Пусть имеется прямоуголь­ная решетка атомов с расстояниями а, b, с в трех направлениях. (Если вам больше по душе кубическая решетка, примите все расстояния равными друг другу.) Предположим также, что ам­плитуда прыжка к соседу в направлении х есть iA_x / h; ампли­туда прыжка в направлении у есть iA_y/h, а амплитуда прыжка в направлении z есть iA_z/h. Как же описать базисные состоя­ния? Как и в одномерном случае, одно базисное состояние — это когда электрон находится близ атома с координатами х, у, z, где (х, у, z) — одна из точек решетки. Если выбрать начало координат в одном из атомов, то все эти точки придутся на

х=n_ха, y=n_yb и z=n_zс,

где n_х, n_y, n_z — три целых числа. Вместо того чтобы ставить при х, у и z их номера, будем просто писать х, у, z, имея в виду, что они принимают лишь такие значения, которые бывают у то­чек решетки. Итак, базисное состояние изображается символом | электрон в х, у, z>, а амплитуда того, что электрон в неко­тором состоянии |y> окажется в этом базисном состоянии, есть

С (х, у, z)=< электрон в х, у, z |y>.

Как и прежде, амплитуды С (х, у, z) могут меняться во вре­мени. При наших предположениях гамильтоновы уравнения обязаны выглядеть следующим образом:

Хоть это и выглядит громоздко, но вы сразу, конечно, поймете, откуда взялось каждое слагаемое.

Опять попробуем найти стационарное состояние, в котором все С меняются со временем одинаково. И снова решение есть экспонента

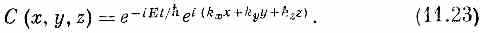
Если вы подставите это в (11.22), то увидите, что оно вполне подойдет, если только энергия Е будет связана с k_x, k_y и k_z следующим образом:

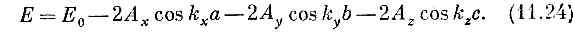
Теперь энергия зависит от трех волновых чисел k_x, k_y, k_z, которые, кстати, есть компоненты трехмерного вектора k.

И действительно, (11.23) можно переписать в векторных обо­значениях:

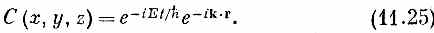
Амплитуда меняется как комплексная плоская волна, которая движется в трехмерном пространстве в направлении k с волно­вым числом k = (k ² _x+k ² _y+ k ² _z)^1/2.

Энергия, связываемая с этими стационарными состояниями, зависит от трех компонент k сложным образом, подчиняясь уравнению (11.24). Характер изменения Е зависит от относи­тельных знаков и величин А_х,А_у и А_z. Если вся эта тройка положительна и если нас интересуют лишь маленькие k, то зависимость оказывается сравнительно простой.

Разлагая косинус, как и раньше [см. (11.16)], мы теперь придем к

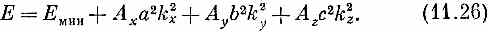
В простой кубической решетке с расстоянием а между узлами следует ожидать, что и А_х, и А_y, и А_г будут все равны друг другу (скажем, равны А), так что получилось бы

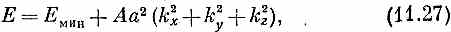
или

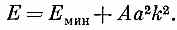
А это как раз совпадает с (11.16). Повторяя те же рассуждения, что и тогда, мы пришли бы к заключению, что электронный пакет в трех измерениях (составленный путем суперпозиции множества состояний с почти одинаковыми энергиями) также движется на манер классической частицы, обладающей некото­рой эффективной массой.

В кристалле не с кубической, а с более низкой симметрией (или даже в кубическом кристалле, но таком, в котором состоя­ние электрона около атома несимметрично) три коэффициента А_х, А_y и A_z различны. Тогда «эффективная масса» элект­рона, сосредоточенного в узкой области, зависит от направле­ния его движения. Может, например, оказаться, что у него раз­ная инерция при движении в направлении х и при движении в направлении у. (Детали такого положения вещей иногда описываются с помощью «тензора эффективной массы».)

Дата добавления: 2015-06-04