Основные общезначимости алгебры предикатов

1.

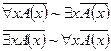
2.

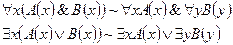
3.

4.

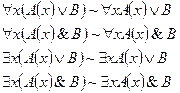
5.

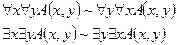
Раздел III. ЛОГИЧЕСКИЕ ИСЧИСЛЕНИЯ

Широкое использование аксиоматического метода в построении математических теорий стало одной из важных причин появления и развития математической логики. При таком подходе выбирается система основных неопределяемых понятий и отношений между ними, далее, постулируется система свойств основных понятий и отношений, называемых аксиомами. Новые понятия теории вводятся через основные или ранее определенные, а утверждения выводятся из аксиом или из ранее доказанных утверждений.

Логическим исчислением принято называть синтаксическую (т.е. формализованную аксиоматическую) теорию математической логики. Описание всякого исчисления I включает:

1) описание алфавита A(I), т.е. множества символов, используемых для построения формул теории, множество произвольных последовательностей символов алфавита обозначим W(I);

2) описание языка E(I) Ì W(I), т.е. правил построения допустимых последовательностей символов (слов) в алфавите, называемых формулами;

3) задание системы аксиом Ax(I) Ì E(I) – некоторого множества истинных формул, называемых аксиомами;

4) определение правил вывода R(I), позволяющих из одних истинных формул получать другие формулы рассматриваемой синтаксической теории.

Часто для записи правил вывода используют сокращенную схему, они выражаются в следующих терминах.

“Если формулы U, B,... истинны, то по правилу вывода R_i формулы M, N,... также истинны”. Такие утверждения записываются в виде схемы:

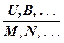i.

Указанием аксиом и правил вывода мы полностью определили понятие истинной, или выводимой в исчислении высказываний, формулы. Пользуясь правилами вывода, мы можем, исходя из аксиом, конструировать новые истинные формулы и получать, таким образом, каждую истинную формулу. Формула B называется доказуемой (теоремой в исчислении высказываний), что обозначается ú- B, если существует конечная последовательность формул

B₁, B₂,..., B_t, (1)

в которой каждая из формул B_i является либо аксиомой, либо, получена по правилам вывода из некоторых предыдущих формул последовательности (1). Эта последовательность называется доказательством формулы (теоремы).

Мы будем говорить, что формула B выводима из формул U₁, U₂,..., U_n в формальной теории, если формулу B можно вывести используя правила вывода, приняв за исходные формулы U₁, U₂,..., U_n и все истинные в данном исчислении формулы. То есть, формула B выводима из формул U₁, U₂,..., U_n, называемых исходными, что записывается символически как

U₁, U₂,..., U_n ú- B,

если существует такая конечная последовательность формул (1), что B_t есть B и для каждой формулы B_i выполнено одно из условий:

1) B_i есть посылка или теорема исчисления;

2) B_i получена из некоторых предыдущих формул последовательности (1) по правилам вывода.

Последовательность (1) называется в этом случае выводом формулы B из системы посылок U₁, U₂,..., U_n.

Дата добавления: 2015-06-04