Математические софизмы

Логические софизмы

Напомним, что софизмом называется умышленно ложное умозаключение, которое имеет видимость правильного.

Логические софизмы - софизмы, ошибки которых заключаются в неправильных рассуждениях.

Например:

«Полупустое тоже, что и полуполное»

Доказательство:

Полупустое есть то же, что и полуполное. Если равны половины, значит, равны и целые. Следовательно, пустое есть то же, что и полное

Ошибка: полупустое не является половиной чего либо пустого, а является чем либо наполовину наполненным.

Рассмотрим такой софизм с названием «ВОР». Он формулиру­ется в рассуждении, которое призва­но убедить нас, что вор делает бла­гое дело. На то ведь он и софизм, чтобы с помощью своей софисти­ческой логики доказывать то, что является недоказуемым.

«Вор приобретает лишь хоро­шее.

Приобретать, а равно и делать хорошее — это благо.

Значит, вор делает благо».

Изъян софизма заметен с перво­го взгляда: приобретать хорошее и делать хорошее — это не только не равнозначные понятия, но даже и не синонимы.

Вот еще один софизм «УЧЕНИ­КИ», в котором из верных посылок получается ложное заключение:

«Все внимательные ученики хоро­шо усваивают уроки.

Некоторые ученики внимательны.

Все ученики хорошо усваивают уроки».

Математический софизм – удивительное утверждение,

в доказательстве которого кроются незаметные,

а подчас и довольно тонкие ошибки.

Мартин Гарднер

Кроме логических софизмов широко известны также и матема­тические. Математические софизмы способствовали и способствуют повышению строгости в математических рассуждениях, содействовали и содействуют более глубокому уяснению понятий и методов математики. На наш взгляд их роль в развитии математики сходна с той ролью, какую продолжают играть до сегодняшнего дня непреднамеренные ошибки в математических доказательствах, допускаемые даже выдающимися математиками.

Рассмотрев различный материал по теме исследования, мы узнали, что софистика основывалась на понятиях логики, её законах, которые основывались на ложных предположениях. А вот допустим, софизм основан на преднамеренном ложном умозаключении, но если смотреть его поверхностно, то оно кажется истинным.
В ходе работы мы узнали, что Джордж Буль тоже основывался на понятии логики в своей алгебре. Он оперировал понятиями ложно и истинно.
А ведь современная вычислительная техника точно так же оперирует понятиями ложно и истинно. Кибернетика как наука, этим и занимается.
Получается, что учения софистов мы используем в современной жизни, особенно цифровой технике, ЭВМ.

Выделяют три вида математических софизмов:

Ø Арифметические

Ø Алгебраические

Ø Геометрические

Обычно в математических софизмах скрыто выполняются зап­рещенные действия или не учитыва­ются условия применимости пра­вил, формул или теорем. Весьма ин­тересно найти ошибку в рассужде­нии, которая приводит к абсурдно­му выводу, причем это не всегда лег­ко и просто сделать.

а) Арифметические софизмы

Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.

Примерами арифметических софизмов могут служить следующие:

1) «Дважды два – пять».

Доказательство:

Пусть исходное соотношение - очевидное равенство:

4:4= 5:5 (*).

Вынесем за скобки общий множитель каждой чести (*) равенства, и мы получим:

4·(1:1)=5·(1:1) (**)

Тогда разложим число 4 на произведение 2 ·2.

Получаем (2·2)· (1:1)=5·(1:1) (***)

Наконец, зная, что 1:1=1, мы из соотношения (**) устанавливаем: 2·2=5.

Ошибка: ошибка заключается в том, что нельзя было выносить множитель за скобки в уравнение (**)

2) В то время когда наши мамы и папы были детьми, то есть в советские времена,

существовала такая денежная единица как рубль, которая равнялась 100 копейкам. Так вот один из софизмов говорит нам обратное.

«Один рубль не равен ста копейкам».

Доказательство:

Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. Если a=b, c=d, то ac=bd.

Применим это положение к двум очевидным равенствам

1 р.=100 коп. (*)

10р.=10·100коп.(**)

Перемножая эти равенства почленно, получим 10 р.=100000 коп.

Наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп.

таким образом, один рубль не равен ста копейкам.

Ошибка: ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.

3) Докажем, что 5 = 6.

Легко проверить справедли­вость равенства: 35 + 10 - 45 = 42+ 12-54.

Вынеся общий множитель за скобки, его можно записать так:

5 • (7 + 2- 9) = 6 • (7 + 2 - 9).

Как мы видим, произведения равны и вторые множители тоже рав­ны, значит, и первые множители должны быть равны, т. е. 5=6.

Ошибка: ошибка в этих рас­суждениях состоит в том, что мы сделали вывод о равенстве первых множителей у равных произведе­ний при условии равенства вторых множителей, что не всегда верно. Такое утверждение справедливо лишь тогда, когда эти равные вто­рые множители отличны от нуля, и мы можем обе части равенства разделить на это число. В случае же нуля всегда а ·0 = b ·0 = 0 при любых а и b, так что вовсе не обяза­тельно, чтобы а=b.

4) “Единица равна двум”

Простым вычитанием легко убедиться в справедливости равенства

1 - 3 = 4 - 6.

Добавив к обеим частям этого равенства число 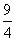, получим новое равенство

1- 3 + 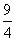= 4-6+ ,

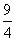в котором, как нетрудно заметить, правая и левая части представляют собой полные квадраты, т. е.

(1- 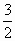) =(2- )

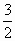Извлекая из правой и левой частей предыдущего равенства квадратный корень, получаем равенство:

1- 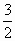=2-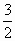

откуда следует, что

1=2.

б) Алгебраические софизмы

Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.

1) Докажем, что 4 = 5.

Возьмем два числа а = 4 и b = 5, их полусумму обозначим через с = (а+b)/2.

Тогда а = 2с- b и 2с-а = b.

Перемножив эти равенства по­членно, получим:

а² - 2ас = b ² - 2 b с.

Прибавив к обеим частям по с², получим:

а² - 2 ас + с² = b ²- 2 b с + с²

или (а - с)² = (b - с)².

Значит, а-с=b-с, откуда а = 6, то есть 4 = 5.

Ошибка: Если квадраты чисел равны, то сами числа не обязатель­но равны, они могут быть и проти­воположными. Равенство а-с= b-с в данном случае неверно, должно быть а-с= b-с или а - с = с - b.

Общий вид: “Все числа равны между собой”

Возьмём два произвольных неравных между собой числа а и b и запишем для них очевидное тождество:

а² -2ab+b² = b² -2ab+ а²

Слева и справа стоят полные квадраты, т. е. можем записать

(а-b)² = (b-а)². (*)

Извлекая из обеих частей последнего равенства квадратный корень, получим:

а - b = b - a (**)

откуда 2а = 2b или окончательно a=b.

Ошибка:

2) Докажем, что число 0 (нуль) больше любого числа а.

Если число а отрицательное, то утверждение очевидно.

Пусть а — сколь угодно боль­шое положительное число. Ясно, что а - 1 < а.

Умножим обе части этого неравенства почленно на - а, получим:

- а² + а< - а².

Прибавив к обеим частям полу­ченного неравенства по а ², получим: - а² + а + а² < - а² + а ², то есть а < 0.

Следовательно, любое, даже сколь угодно большое положитель­ное число а меньше 0.

Ошибка: При умножении обеих частей неравенства на -а, то есть на отрицательное число, знак неравенства необходимо поменять на противоположный.

3) Докажем, что любое число рав­но 0.

Рассмотрим сумму: а - а + а - а + а - а + а -...

Эту сумму можно представить двояко:

(а-а) + (а-а) + (а-а) +... =0 или а-(а-а)-(а-а)-(а-а)-... =а.

Левые части этих выражений равны, значит, равны и правые, и, следовательно, а - 0.

Ошибка: В первом выраже­нии рассматривается четное количе­ство слагаемых, а во втором — не­четное, поэтому результаты отлича­ются на а.

в) Геометрические софизмы

Геометрические софизмы основаны на ошибках связанных с геометрическими фигурами и действиями над ними.

1) «Хорда, не проходящая через центр окружности, равна диаметру».

Доказательство:

Пусть в окружности проведен диаметр АВ. Через точку В проведем любую хорду ВЕ, не проходящую через центр, затем через середину этой хорды D и точку А проведем новую хорду АС. Наконец, точки Е и С соединим отрезком прямой.

Рассмотрим ∆ АВD и ∆ЕDС. В этих треугольниках: ВD = DЕ (по построению), <А=

= <Е (как вписанные, опирающиеся на одну и ту же дугу). Кроме того, <ВDА=

= <ЕDC (как вертикальные). Если же сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны. Значит, ∆ ВDА= ∆ЕDC, а в равных треугольниках против равных углов лежат равные стороны. Поэтому, АВ=ЕС.

Ошибка: ошибка заключается в неправильном применении теоремы о равенстве треугольников. По теореме о признаке равенства треугольника: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. А в нашем случае, < А не прилежит к стороне ВD.

2) «Спичка вдвое длиннее телеграфного столба».

Доказательство:

Пусть а длина спички и b - длина столба. Разность между b и a обозначимчерез c.

Имеем b - a = c, b = a + c.

Перемножим два этих равенства по частям, находим: b² - ab = ca + c².

Вычтем из обеих частей bc. Получим: b²- ab - bc = ca + c² - bc, или

b(b - a - c) = - c(b - a - c), откуда

b = - c, но c = b - a, поэтому b = a - b, или a = 2b.

Ошибка: ошибка заключается в том,что вравенстве выражений b(b-a-c)=-c(b-a-c)

производится деление на 0.

Это лишь несколько из множе­ства известных еще с древности и дошедших до нас логических и ма­тематических софизмов. Софизмы способствовали повышению строгости математических рассуждений и содействовали более глубокому уяснению понятий и методов математики. Для изучающих математику софизмы полезны еще и тем, что их разбор развивает логическое мышление.

Обнаружить ошибку в софизме – это значит осознать ее, а осознание ошибки предупреждает от повторения ее в других математических рассуждениях.

Классификация, рассмотренных нами софизмов, по допущенным в них ошибках и темах, при изучении которых, на наш взгляд их можно использовать представлена нами в приложении.

Заключение

Итак, софизм – это изобре­тение человеческого разума, с помо­щью которого можно доказать всё, что угодно. Впрочем, и опровергнуть можно тоже всё. Недаром вели­кий русский ученый И. П. Павлов говорил, что «правильно понятая ошибка – это путь к открытию».

Поначалу может показаться, что существует мало софизмов, или что они не используются в жизни, то есть бесполезны. Но это не так. Существует огромное множество разных видов софизмов. И математические софизмы – всего лишь небольшая их часть. За свою жизнь человек слышит десятки софизмов, не умея отличить их от правдивых утверждений, и даже не зная, что вообще означает слово софизм.

Понять софизм, то есть решить его, получается не сразу. Поначалу, чтобы решить некоторые софизмы, приходилось по многу раз их внимательно перечитывать, вдумываться и всматриваться, например в софизме «Хорда, не проходящая через центр окружности, равна диаметру» нам пришлось долго искать ошибку. Теперь, к концу работы над исследованием ошибки нам стали находиться быстрее. Мы считаем, что хорошо развитое логическое мышление может помочь не только в решении задач, но и в обычной жизни. Вообще, решение софизмов – интересное и познавательное занятие. Им можно заниматься как целенаправленно, так и в свободное время для собственного удовольствия, как например решение сканвордов или судоку.

Вот такие они софизмы и вот такая она – софистика. И в ней есть своя логика, может, это не логика с большой буквы, но хотя бы своя софистическая логика. А это достойно того, чтобы к этой логике приглядеться, хотя она и замешана на логических ошибках. Но ведь логика изучает законы не только правильного, но и неправильного мышления. Ибо нельзя познать ис­тину, не познав ложь, как нельзя постичь добро, не ведая зла. В мире все так: свет соседствует с тенью, жизнь – со смертью, а ис­тина – с ложью.

Мы пришли к выводу, что математические софизмы развивают наблюдательность и вдумчивость, приучают тщательно следить за точностью формулировок, правильностью записей и чертежей, за законностью выполняемых операций. Ну, и, наконец, разбор софизмов просто увлекателен – это изящная гимнастика для ума любого человека.

Так как мы не сильны в создании собственных софизмов, то для исследования в работе мы воспользовались софизмами из книги [3]

Дата добавления: 2015-06-04