Равноугольные конические проекции на эллипсоиде

Из примеров таблиц 6.1 и 6.2 мы видим, что в конических проекциях по мере удаления от параллели касания или сечения к югу и к северу масштаб по параллели непрерывно увеличивается.

Чтобы сделать масштаб одинаковым вокруг каждой точки, т.е. обеспечить на карте и глобусе подобие бесконечно малых фигур, а, следовательно, и равенства углов, следует видоизменить равнопромежуточную проекцию так, чтобы по мере увеличения масштаба вдоль параллелей соответственно увеличивался масштаб по меридианам.

Впервые теорию равноугольных конических проекций разработал в 1772г. Л. Ламберт.

Равноугольная коническая проекция Ламберта по отношению к равнопромежуточной конической проекции представляет то же самое, что равноугольная цилиндрическая проекция Г. Меркатора (см. 5.4) по сравнению с простой цилиндрической проекцией Генриха Мореплавателя (см. 5.2)

Для достижения равноугольности проекции необходимо и достаточно обеспечить равенство увеличений вдоль параллели и меридиана, т.е. .

На основании (6.2) и (6.5) для эллипсоида можем записать

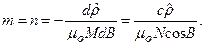(6.26)

Знак минус для взят потому, что с увеличением широты радиус 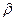на карте убывает.

Из выражения (6.26) найдём радиус как явную функцию широты как это следует из общего уравнения (4.8). Для этого представим (6.26) в виде

.

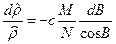Подставим вместо 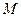и их значения из (2.4) и (2.5). В результате получим

.

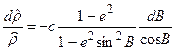Интегрируя левую и правую части, получим

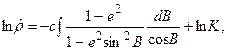(6.27)

где 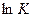- постоянная интегрирования.

Для упрощения подынтегрального выражения умножим 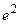в числителе на величину 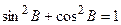. Тогда выражение (6.27) примет вид

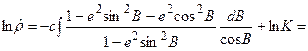
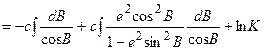. (6.28)

Введем обозначения

тогда

,

.

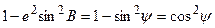С учетом этих обозначений можем записать

.

Известно [ ]

.

Следовательно, имея также в виду, что логарифм дроби равен разности логарифмов числителя и знаменателя, можем записать

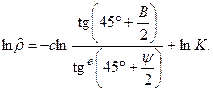(6.29)

Введем обозначения

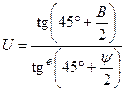. (6.30)

Подставляя (6.30) в (6.29), получим

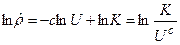
и следовательно

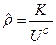. (6.31)

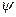Раскроем геометрический смысл постоянной интегрирования К. Для этого примем . Соответственно также будет равна нулю. Подставляя эти значения в (6.29), найдём

,

откуда на основании (6.31) можем найти радиус экватора

.

На полюс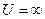е и . Следовательно, полюс в этой проекции изобразится точкой в отличие от равнопромежуточной проекции, где полюс изображается полярной линией.

На основании (6.6) радиус параллели наименьшего масштаба равен

а коэффициент пропорциональности, исходя из (6.15) равен

.

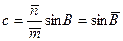Рассмотрим расчет равноугольной конической проекции для карты Украины в масштабе 1:1000000, приняв широту параллели касания .

Предварительно определяем 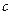и

.

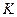
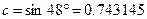На основании (6.6) и (б.30) можем записать

,

откуда имея в виду, что на параллели касания 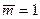, имеем

.

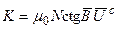Определим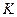

,

,

.

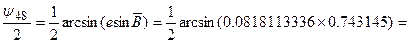
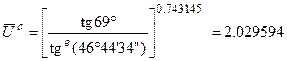Все остальные данные приведены в таблице 6.3.

Таблица 6.3

Широта
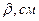
44°	619.86	1.0024	1,0048
45°	608.73	1.0013	1,0026
46°	597.60	1,0006	1,0012
47°	586.48	1,0001	1,0003
48°	575.36	1,0000	1,0000
49°	564.24	1,0001	1,0003
50°	553.12	1,0006	1,0012
51°	541.98	1,0014	1,0028
52°	530.83	1,0025	1,0050

Как и в случае равнопромежуточных проекций, задавая применительно к расположению конкретной картографируемой территории широту параллели касания , можем получить множество равноугольных проекций.

Из таблицы 6.3 следует, что за равноугольность проекции придётся расплачиваться искажениями расстояний по меридиану и большими искажениями площадей до 50 м²/га.

Рассмотрим теперь равноугольную проекцию на секущем конусе.

Для параллелей сечения . На основании (6.26), принимая во внимание (6.31) и (6.23), можем записать

. (6.32)

Сократив это выражение на будем иметь

Прологарифмируем это равенство. В результате получим

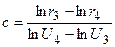. (6.33)

Подстановкой 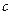в (6.32) найдем 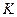с контролем

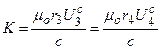. (6.34)

Величины 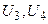определятся из выражения (6.30)

Широту параллелей сечения можно вычислить по формуле (6.20) с последующим округлением до целого градуса.

Используя полученные формулы рассчитаем проекцию для карты Украины в масштабе 1:1000000.

По формуле (6.20) находим .

Из (6.33) получим 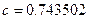, а из (6.30) .

По формуле (6.34) находим .

Все остальные данные приведены в таблице 6.4.

Таблица 6.4

44°	618,737	1,0010	1,0020
45°	607,620	1,0000	1,0000
46°	596,510	0,9992	0,9984
47°	585,405	0,9988	0,9976
48°	574,301	0,9986	0,9972
49°	563,196	0,9988	0,9976
50°	552,086	0,9992	0,9984
51°	540,967	1,0000	1,0000
52°	529,835	1,0011	1,0022

Сравнивая параметры, приведённые в таблицах 6.3 и 6.4, приходим к выводу, что замена касательного конуса секущим уменьшает искажения длин и площадей в 1,7 раз.

Если заменить эллипсоид шаром, формулы для расчёта проекции упрощаются. Так как то 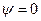и выражение (6.30) принимает вид

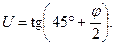
Соответственно

.

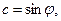
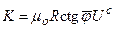Все остальные формулы можно применить, заменив 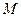и на .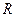

Дата добавления: 2015-06-04