Равновеликие конические проекции

Рассмотрим сначала эти проекции на шаре.

В конических проекциях меридианы и параллели пересекаются под прямым углом 90°. Вот почему на основании (4.2) можем записать

.

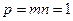Подставляя вместо и 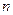их значения из (6.2) и (6.5) и приняв ,имеем

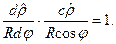
откуда находим

.

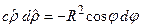Интегрируя левую и правую части этого выражения, найдём

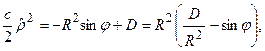
где 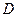- постоянная интегрирования, имеющая ту же размерность, что и , т.е. м² или км².

Введём новую постоянную

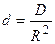, (6.35)

с учетом (6.35) получим окончательно для радиуса

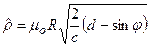. (6.36)

Таким образом, мы получим функцию, определяющую радиус параллели в явном виде.

Для практического использования проекции помимо необходимо знать также) 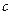и .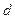

Задавая по тем или иным критериям эти величины, мы будем иметь различные конические равновеликие проекции.

Определим широту параллели, где увеличение будет наименьшим. Для этого подставим в выражение (6.5) значение из (6.36)

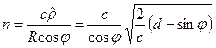. (6.37)

Возведем левую и правую части (6.37) в квадрат

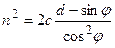. (6.38)

Исследуем функцию (6.38) на минимум, полагая, что минимуму 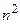соответствует минимум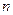

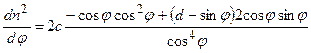
или

.

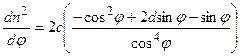Заменим в числителе 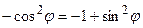. Тогда

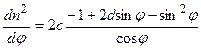. (6.39)

Для определения широты 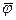, на которой 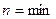, приравняем производную к нулю. Знаменатель в (6.39) не может быть больше единицы. Вот почему для того, чтобы дробь (6.39) была равна нулю, необходимо, чтобы числитель равнялся нулю. В результате получим квадратное уравнение

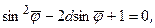(6.40)

решением которого будет выражение

.

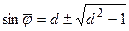Постоянная 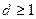, так как в противном случае 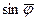стал бы мнимой величиной. С другой стороны перед корнем необходимо оставить только знак минус, так как 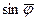не может быть больше единицы. В результате получаем единственное решение, из которого при заданном 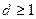можем определить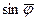

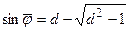. (6.41)

И наоборот, по заданной широте 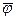из (6.40) можно найти d

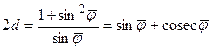. (6.42)

Найденное из (6.41) единственное значение 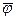соответствует минимуму 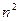, а следовательно и n.

Коэффициент пропорциональности с найдём из выражения (6.38), полагая, что на параллели касания с широтой .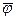

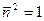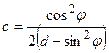. (6.43)

Как пример, рассчитаем параметры равновеликой конической проекции для карты Украины в масштабе 1:1000000, приняв широту параллели касания 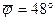и радиус шара .

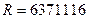Из (6.42) найдём

,

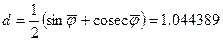а из (6.43)

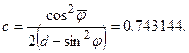
Все остальные данные приведены в таблице 6.5.

Сравнивая эту таблицу с таблицей 6.1, можно заключить, что при примерно одинаковом растяжении по параллели равновеликость достигается за счет сжатия по меридиану и за счет увеличения угловых искажений на крайних параллелях.

Чтобы уменьшить искажения, касательный конус можно заменить секущим.

Таблица 6.5

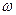
44°	618,103	0,9977	1,0023	0°15'
45°	607,003	0,9987	1,0013	0°09'
46°	595,893	0,9994	1,0006	0°04'
47°	584,778	0,9998	1,0002	0°
48°	573,658	1,0000	1,0000	0°
49°	562,539	0,9998	1,0002	0°
50°	551,424	0,9994	1,0006	0°04'
51°	540,315	0,9985	1,0015	0º10'
52°	529,218	0,9974	1,0027	0º18'

Как известно, в секущёй проекции на параллелях сечения с широтой 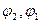имеем 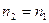. Вот почему, на основании (6.4) можем записать

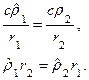
Возведя это выражение в квадрат и подставив значение из (6.36), найдём

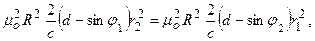
откуда

,

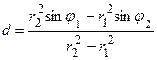но 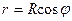, следовательно

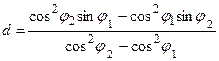. (6.44)

Введём обозначения

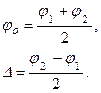(6.45)

Выполнив в (6.44) преобразования тригонометрических функций с учетом обозначений (6.45), получим окончательно

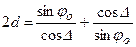. (6.46)

Для определения 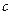воспользуемся равенством (6.4) и возведём его в квадрат

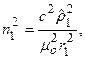
откуда

.

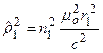Но согласно (6.36)

.

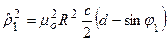Следовательно

.

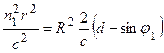Подставив в это выражение вместо 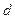его значение из (6.46), а вместо 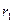- равное ему значение 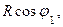выполним преобразования тригонометрических функций с учетом обозначений (6.45). В результате будем иметь

.

Но, так как для параллели сечения n=1, получим окончательно

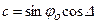. (6.47)

Если задать параллели сечения 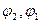, то выражения (6.45), (6.46), (6.47), (6.36) и (6.37) полностью определяют параметры равновеликой конической проекции на секущем конусе.

Рассмотрим расчет этой проекции для карты Украины в масштабе 1:1000000.

Широту параллелей сечения 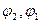определим из выражения (6.20), приняв Т=7. Широта крайних параллелей 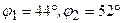. Полученные значения 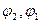округлим до целого градуса.

В результате имеем .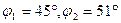

Из выражений (6.45) находим 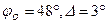, из (6.46) 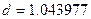, а из (6.47) .

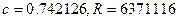Все остальные данные приведены в таблице 6.6.

Таблица 6.6

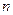
44°	618,162	0,9990	1,0010	0°07'
45°	607,048	1,0000	1,0000	0°
46°	595,924	1,0007	0,9993	0°05'
47°	584,793	1,0012	0,9988	0°08'
48°	573,659	1,0014	0,9986	0°10'
49°	562,525	1,0012	0,9988	0°08'
50°	551,393	1,0008	0,9992	0°05'
51°	540,269	1,0000	1,0000	0°
52°	529,155	0,9988	1,0012	0°08'

Сравнивая эти данные с таблицей 6.5, можно заключить что искажение расстояний на крайних параллелях уменьшилось почти в 2 раза за счёт увеличения искажений расстояний на средних параллелях. Но в целом не превышает 1,4 м на км.

Искажение углов стало более равномерным и не превышает 10’. При решении многих картометрических задач такие искажения углов можно считать пренебрегаемо малыми.

Чтобы построить равновеликую коническую проекцию для эллипсоида, необходимо общие уравнения проекции (4.8) и (4.9) применить к земному эллипсоиду.

Есть и дугой более простой путь: сначала мысленно изобразить эллипсоид на шаре с сохранением площадей, а затем применить выведенные раннее формулы для шара.

При этом геодезические координаты B и L точек нужно заменить сферическими координатами изображения этих же точек на шаре 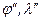, поставив условие, чтобы параллели эллипсоида соответствовали параллелям шара, а меридианы эллипсоида изображались меридианами шара, т.е.

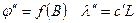. (6.48)

Масштабы m и n найдём, взяв отношения элементов меридиана и параллели шара к соответствующим элементам эллипсоида, которые представлены выражениями (6.2) и (6.4)

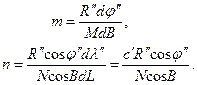(6.49)

Так как направление меридиана и параллели – главные направления эллипса искажений, то условие равновеликости mn=1. Подставив в это условие значение m и n из (6.49), найдём

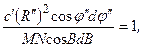
откуда

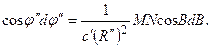
Интегрируя, получим

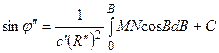
или

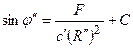, (6.50)

где 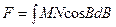- часть поверхности эллипсоида, ограниченная экватором, параллелью с широтой и двумя меридианами с разностью долгот 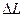в один радиан.

Этот интеграл после подстановки M и N из (2.4), (2.5) может быть приведён к виду

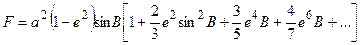. (6.51)

В формулу (6.50) входят три пока неизвестных параметра 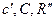, которые можно определить, поставив следующие условия:

1) долготы не должны изменяться, тогда 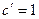и ;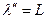

2) чтобы экватор эллипсоида изображался экватором шара, т.е. при должно быть 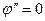и ;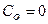

3) чтобы полюс эллипсоида изображался полюсом шара, т.е. при 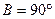было бы 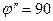, т.е. согласно (6.50)

,

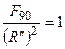откуда найдём 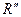, подставив значение F из (6.51) при 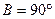в (6.50)

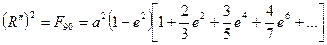. (6.52)

Для эллипсоида Красовского .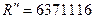

Подставим наёденные значения 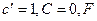из (6.51) и 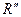из (6.52) в (6.50). В результате получим формулу для вычисления равновеликой широты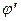

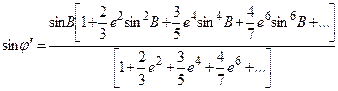. (6.53)

Имея широту 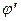, для расчета проекции мы можем воспользоваться выведенными ранее формулами (6.42), (6.36), (6.37) и (6.43).

Таким образом решается задача построения равновеликой конической проекции на эллипсоиде.

Дата добавления: 2015-06-04