Задачи оптимизации

Планирование правовой, производственно-хозяйственной, управленче­ской и административной деятельности приводит к задачам, имеющим мно­жество допустимых решений. Из этого множества решений нужно выбрать такое, которое бы оптимальным образом учитывало внутренние возможности и внешние условия для хозяйствующего или управляющего субъекта (выбор производственной программы, прикрепление к поставщикам, маршрутиза­ция, раскрой материалов, приготовление смесей и т.д.).

Суть принципа оптимальности состоит в стремлении выбрать такое планово-управленческое решени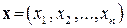е , где - его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта. С этой целью нужно выбрать некоторый критерий оптимальности экономического или правового показателя, позволяющего сравнивать эффективность тех или иных планово-управленческих решений («максимум прибыли», «минимум затрат», «максимум рентабельности» и т.д.). При этом выбор планово-управленческого решения осуществляется из некоторой области возможных (допустимых) решений D; эту область называют также областью определения задачи.

На практике принцип оптимальности в планировании и управлении означает решить экстремальную задачу об отыскании максимума или минимума функции

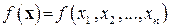
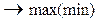
при ограничениях

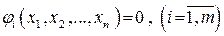
Вектор 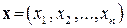называется допустимым решением, или планом задачи оптимального программирования, если он удовлетворяет системе ограничений. А то допустимое решение 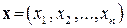, которое доставляет максимум или минимум целевой функции 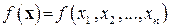, называется оптимальным планом (решением) задачи.

Программирование – это процесс распределения ресурсов.

Математическое программирование - это использование математиче­ских моделей и методов для решения проблем программирования.

Если целевая функция является линейной, а система ограничений на ресурсы представляет собой систему линейных взаимосвязей между пере­менными, то такая задача является задачей линейного программирования.

Задача линейного программирования о смесях

Стандартом предусмотрено, что октановое число автомобильного бензина А-76 должно быть не ниже 76, а содержание серы в нем – не более 0,3%. Для изготовления такого бензина на заводе используется смесь из четырех компонентов. Данные о ресурсах смешиваемых компонентов, их себестоимости и их октановом числе, а также о содержании серы приведены в таблице 12.

Таблица 12

Характеристика	Компонент автомобильного бензина
№ 1	№2	№ 3	№4
Октановое число
Содержание серы, %	0,35	0,35	0,3	0,2
Ресурсы, т
Себестоимость, у.е./т

Приказом директора завода-изготовителя установлен следующий расход каждого компонента: 1 – 550 т, 2 – 10 т, 3 – 150 т, 4 – 290 т. Требуется определить, сколько на самом деле тонн каждого компонента следует использовать для получения 1000 т автомобильного бензина А-76, чтобы его себестоимость была минимальной. Какова упущенная выгода предприятия при производстве каждых 1000 т бензина при таком решении дирекции?

Ход работы

Пусть 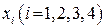– количество в смеси компонента с номером i. С учетом этих обозначений задача минимума себестоимости принимает вид:

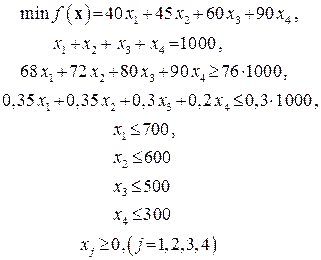
Первое функциональное ограничение отражает необходимость получения заданного количества смеси (1000 т), второе и третье – ограничения по октановому числу и содержанию серы в смеси, остальные – ограничения на имеющиеся объемы соответствующих ресурсов (компонентов). Прямые ограничения очевидны, но принципиально важны для выбора метода решения. Для решения задачи средствами Excel необходимо составить таблицу 13.

Решение задачи о смесях средствами Excel Таблица 13
Переменные	Значения	Критерий и ограничения	Результаты расчетов	Знак отношения	Ресурс
X1		Целевая функция	=40*B3+45*B4+60*B5+90*B6
X2		Ограничение 1	=СУММ(B3:B6)	=
X3		Ограничение 2	=68*B3+72*B4+80*B5+90*B6	=>
X4		Ограничение 3	=0,35*B3+0,35*B4+0,3*B5+0,2*B6	<=
		Ограничение 4	=B3	<=
		Ограничение 5	=B4	<=
		Ограничение 6	=B5	<=
		Ограничение 7	=B6	<=

Для решения задачи средствами Excel нужно воспользоваться программой-надстройкой Поиск решения, расположенной в пункте меню Сервис.

В открывшемся диалоговом окне следует установить:

- адрес целевой ячейки;

- диапазон адресов изменяемых ячеек;

- систему ограничений.

Добавления, изменения и удаления ограничений производятся с помощью кнопок Добавить, Изменить, Удалить. Кнопка Параметры открывает окно, в котором следует установить флажок Неотрицательные решения. Для нахождения оптимального решения следует нажать кнопку Выполнить.

Диалоговое окно Результаты поиска решения позволяет:

- сохранить на текущем рабочем листе найденное оптимальное решение;

- восстановить первоначальные значения;

- сохранить сценарий;

- выдать отчеты по результатам, устойчивости, пределам, необходимые для анализа найденного решения.

Если щелкнуть по кнопке ОК, то на месте исходной таблицы получим таблицу с найденными оптимальными значениями.

Оптимальное решение задачи имеет вид:

.

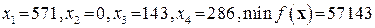Решение дирекции:

.

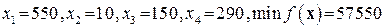Таким образом, упущенная выгода предприятия при производстве каждых 1000 т бензина при таком решении дирекции составляет 407 у.е.

Дата добавления: 2015-06-04