Оценка значимости уравнения регрессии

Скорректированный коэффициент детерминации

Скорректированный коэффициент детерминации содержит поправки на число степеней свободы и определяется выражением:

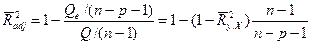(34)

Коэффициент 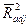также называют адаптированным, нормированным и, иногда не совсем правильно, исправленным выборочным коэффициентом детерминации.

Свойства коэффициента :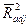

1. .

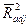
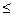
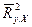2. Коэффициент 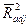при выполнении 5-го условия КЛММР является состоятельной и, в отличие от 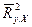, несмещённой оценкой генерального коэффициента детерминации ( [ ] ).

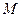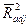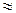
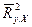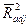
3. 1, но может принимать отрицательное значение.

4. В отличие от 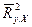, величина 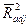может уменьшиться при добавлении в модель новых регрессоров, не оказывающих существенного влияния на зависимую переменную.

Для оценки значимости уравнения регрессии естественно использовать величину:

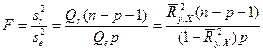, (35)

показывающую, во сколько раз дисперсия, объясненная регрессией, превышает остаточную. При отсутствии какой бы то ни было линейной статистической связи между зависимой и совокупностью объясняющих переменных (при 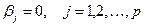) факторная 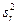и остаточная дисперсия 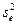дисперсии будут близкими друг к другу и величина 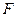будет мала. При этом статистика (33) будет иметь распределение Фишера-Снедекора ( 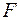-распределение) с 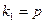и 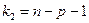степенями свободы.

Следовательно, нулевая гипотеза о незначимости уравнения регрессии в целом (об одновременном равенстве нулю всех коэффициентов при факторных переменных) составляет .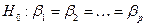

Уровень значимости определяется выражением:

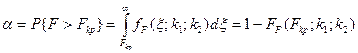. (36)

Доверительный уровень находится по формуле:

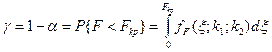. (37)

Критическая точка:

(38)

находится по таблицам критических точек или с помощью стандартных функций в пакетах компьютерных программ.

Нулевая гипотеза 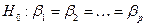применяется в том случае, когда 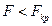и с уровнем значимости 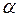делается вывод о том, что уравнение регрессии незначимо.

В противном случае, когда 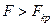с уровнем значимости 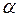делается вывод о том, что уравнение регрессии значимо.

Величина -значения составляет:

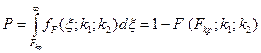. (39)

Дата добавления: 2015-06-04