Краткие теоретические сведения. Аппроксимация функции одной переменной

Цель работы

Аппроксимация функции одной переменной

Лабораторная работа № 1

Введение

B ряде методов, созданных для реализации искусственного интеллекта, используются явные представления знаний и тщательно спроектированные алгоритмы перебора. Отличный от этого подход состоит в построении интеллектуальных программ с использованием моделей, имитирующих нейронные структуры в человеческом мозге или эволюцию разных альтернативных конфигураций, как это делается в генетических алгоритмах и искусственной жизни. Для того чтобы решать сложные и плохо формализуемые задачи и возникло направление, которое называется искусственные нейронные сети.

Искусственные нейронные сети состоят из нейроноподобных элементов, соединенных между собой в сеть. Существуют статические и динамические нейронные сети. В статических нейронных сетях изменение параметров системы происходит по некоторому алгоритму в процессе обучения. После обучения параметры сети не меняются. В динамических нейронных сетях отображение внешней информации, и ее обработка осуществляется в виде некоторого динамического процесса, то есть процесса, зависящего от времени.

Нейронные сети нашли применение практически во всех областях науки и техники. С использованием нейронных сетей успешно решаются многие проблемы бизнеса и финансов. Задачи управления, классификации, распознавания образов, прогнозирования, присущие практически всем прикладным областям, таким как медицина, военное дело, авиация и космос, строительство, все чаще решаются с применением нейросетевых технологий.

В связи с этим необходимо дать студентам, обучающимся современным информационным технологиям, фундаментальное представление об основных понятиях и моделях нейронных сетей, а также научить применять эти знания на практике.

Данные лабораторные работы направлены на вырабатывание практических навыков построения искусственных нейронных сетей в среде MatLab. Особенностью выполнения работ является то, что студент приучается к самостоятельному принятию решений, развиваются его исследовательские способности, что особенно важно в динамично развивающемся мире. В настоящих методических указаниях рассматриваются нейронные сети прямой передачи сигнала, радиальные базисные сети, сеть Кохонена и сеть Хопфилда, являющиеся типовыми технологиями искусственных нейронных сетей.

Научиться работать с сетью прямой передачи сигнала, функция newff [1]. Разобраться с алгоритмом обратного распространения ошибки.

В лабораторной работе рассматривается нейронная сеть с прямой передачей сигнала (с прямой связью) [2], то есть сеть, в которой сигналы передаются только в направлении от входного слоя к выходному, и элементы одного слоя связаны со всеми элементами следующего слоя. Важнейшим для реализации нейронных сетей является определение алгоритма обучения сети.

В настоящее время одним из самых эффективных и обоснованных методов облучения нейронных сетей является алгоритм обратного распространения ошибки, который применим к однонаправленным многослойным сетям. В многослойных нейронных сетях имеется множество скрытых нейронов, входы и выходы которых не являются входами и выходами нейронной сети, а соединяют нейроны внутри сети, то есть скрытые нейроны. Занумеруем выходы нейронной сети индексом 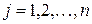, а обучающие примеры индексом 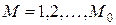. Тогда в качестве целевой функции можно выбрать функцию ошибки как сумму квадратов расстояний между реальными выходными состояниями 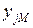нейронной сети, выдаваемых сетью на входных данных примеров, и правильными значениями функции 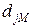, соответствующими этим примерам. Пусть 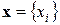– столбец входных значений, где i =1,2,.., n. Тогда 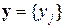– выходные значения, где j =1,2,…, m. В общем случае n ≠ m. Рассмотрим разность , где 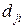– точное (правильное) значение из примера. Эта разность должна быть минимальна. Введем расстояния согласно евклидовой метрике, определив норму

. (1)

Пусть целевая функция имеет вид

. (2)

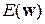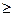Коэффициент ½ выбран из соображений более короткой записи последующих формул. Задача обучения нейронной сети состоит в том, чтобы найти такие коэффициенты , при которых достигается минимум (Е 0).

На рис. 1 показана архитектура нейронной сети с прямой передачей сигнала.

Рис. 1. Схема архитектуры нейронной сети с прямой передачей сигнала

Здесь приняты обозначения, используемые в [1], а именно, ‑ вектор входа, 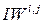, 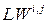‑ матрицы весов входа и выхода, 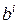‑ смещение, 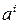‑ выход слоя, ‑ выход сети, tansig (гиперболическая тангенциальная), purelin (линейная) ‑ соответствующие функции активации.

Веса и смещения определяются с помощью алгоритма обратного распространения ошибок [3].

Обучение сети обратного распространения требует выполнения следующих операций:

1. Выбрать очередную обучающую пару из обучающего множества; подать входной вектор на вход сети.

2. Вычислить выход сети.

3. Вычислить разность между выходом сети и требуемым выходом (целевым вектором обучающей пары).

4. Скорректировать веса сети так, чтобы минимизировать ошибку.

5. Повторять шаги с 1 по 4 для каждого вектора обучающего множества до тех пор, пока ошибка на всем множестве не достигнет приемлемого уровня.

Дата добавления: 2015-06-04