Пример решения типовой задачи. Пусть функция задана на промежутках , ; количество точек разбиений по

Пусть функция задана на промежутках , ; количество точек разбиений по 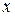есть nx, а по ‑ ny. Тогда, используя следующий алгоритм построения радиальной базисной сети, можно построить график функции :

x1=-1.0; x2=+1.0; y1=-1.5; y2=+1.5;

nx=7; ny=9;

step_x=(x2-x1)/(nx-1); step_y=(y2-y1)/(ny-1);

step_min = min(step_x,step_y);

[x,y]=meshgrid([x1:step_x:x2], [y1:step_y:y2]);

z=exp(-x.^2).*exp(-y.^2);

surf(x,y,z), title('PS. Press<enter>');

pause;

xx=reshape(x,1,nx*ny);

yy=reshape(y,1,nx*ny);

zz=exp(-xx.^2).*exp(-yy.^2);

p=[xx; yy];

t=zz;

goal = 0.0371;

spread = 1.0*step_min;

net = newrb(p,t, goal,spread);

net.layers{1}.size

smlt=sim(net,p);

[zz' smlt']

smltr=reshape(smlt,ny,nx);

surf(x,y,smltr), title('AS. Press<enter>');

Рис. 6 иллюстрирует график исходной функции .

Рис. 6. График исходной функции двух переменных

На рис. 7 показана характеристика точности обучения радиальной базисной сети и допустимая среднеквадратичная ошибка сети Goal=0.0371.

Рис. 7. Характеристика точности обучения в зависимости от количества эпох обучения

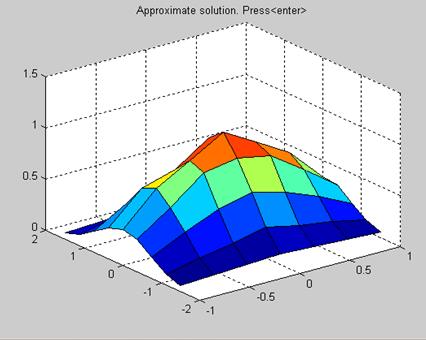
На рис. 8 отображён результат аппроксимации нелинейной зависимости, построенный с помощью радиальной базисной функции.

Рис. 8. Результат моделирования исходной функции

Сопоставляя рис. 6 и рис. 8, можно сделать вывод об удовлетворительности полученных результатов. Лучших результатов можно добиться, варьируя параметры goal и spread.

1.4. Отчёт о выполнении работы

Отчёт о выполнении лабораторной работы №2 должен быть выполнен на листах формата А4 и содержать следующие результаты:

1. Исходные данные – выбор функции двух переменных и области определения функции, построение графика функции (рис. 6);

2. Текст программы с подробными комментариями;

3. Результаты моделирования (рис. 7, 8);

4. Контрольный пример;

5. Объяснение результатов проделанной работы.

Дата добавления: 2015-06-04