Краткие теоретические сведения. Сеть Кохонена, самоорганизующаяся нейронная сеть

Цель работы

Сеть Кохонена, самоорганизующаяся нейронная сеть

Лабораторная работа № 3

Изучить функционирование и процедуру обучения сети Кохонена с помощью функции newc.

Сети Кохонена, или самоорганизующиеся карты (Kohonen maps), предназначены для решения задач автоматической классификации, когда обучающая последовательность образов отсутствует (обучение без учителя). Сеть Кохонена является двухслойной. Она содержит слой входных нейронов и собственно слой Кохонена. Слой Кохонена может быть одномерным, двумерным и трехмерным. В первом случае нейроны расположены в цепочку; во втором – они образуют двумерную сетку (обычно в форме квадрата или прямоугольника), а в третьем – трехмерную систему. Определение весов нейронов слоя Кохонена основано на использовании алгоритмов автоматической классификации (кластеризации или самообучения).

На вход сети подаются последовательно значения векторов , представляющих отдельные последовательные наборы данных для поиска кластеров, то есть различных классов образов, причем число этих кластеров заранее неизвестно. На стадии обучения (точнее самообучения) сети входной вектор 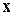попарно сравнивается со всеми векторами всех нейронов сети Кохонена. Вводится некоторая функция близости d (например, в виде евклидова расстояния). Активный нейрон с номером c слоя Кохонена, для которого значение функции близости между входным вектором 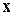, характеризующим некоторый образ, к векторам 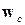максимально, объявляется «победителем». При этом образ, характеризующийся вектором 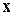, будет отнесен к классу, который представляется нейроном-«победителем».

Рассмотрим алгоритм самообучения сетей Кохонена. Обозначим функцию близости . Выигрывает нейрон c

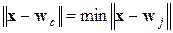. (1)

Близость 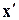и 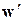можно переделить, пользуясь скалярным произведением, как

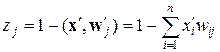. (2)

На стадии самообучения сети Кохонена осуществляется коррекция весового вектора не только нейрона-«победителя», но и весовых векторов остальных активных нейронов слоя Кохонена, однако, естественно, в значительно меньшей степени – в зависимости от удаления от нейрона-«победителя». При этом форма и величина окрестности вокруг нейрона-«победителя», весовые коэффициенты нейронов которой также корректируются, в процессе обучения изменяются. Сначала начинают с очень большой области – она, в частности, может включать все нейроны слоя Кохонена. Изменение весовых векторов осуществляется по правилу

, j= 1,2, …, n, (3)

где 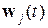- значение весового вектора на шаге t самообучения сети, 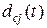- функция близости между нейронами слоя Кохонена и - изменяемый во времени коэффициент шага коррекции. В качестве обычно выбирается монотонно убывающая функция (0< <1), то есть алгоритм самообучения начинается сравнительно большими шагами адаптации и заканчивается относительно малыми изменениями.

В результате n -мерное входное пространство отобразится на m -мерную сетку (слой Кохонена). Это отображение реализуется в результате рекуррентной (итеративной) процедуры самообучения (unsupervised learning). Отличительная особенность этого отображения – формирование кластеров (clusters) или классов. По завершении процесса самообучения на стадии реального использования сети Кохонена неизвестные входные образы относятся к одному из выявленных кластеров (классов) по близости к некоторому весу, принадлежащему определенному кластеру, выявленному на стадии самообучения.

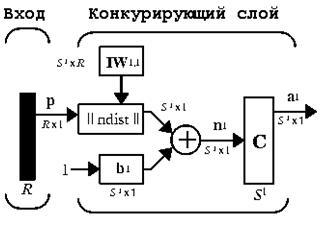
На рис. 9 показана архитектура слоя Кохонена.

Рис. 9. Схема архитектуры слоя Кохонена

Дата добавления: 2015-06-04