Знакочередующиеся ряды. Признак Лейбница

ЗНАКОЧЕРЕДУЮЩИЕСЯ И ЗНАКОПЕРЕМЕННЫЕ РЯДЫ

Рассмотрим важный класс рядов, называемых знакочередующимися. Знакочередующимся рядом называется ряд вида

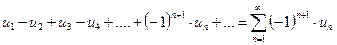, (6.1)

где 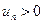для всех 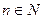(т. е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно).

Для знакочередующихся рядов имеет место достаточный признак сходимости (установленный в 1714 г. Лейбницем в письме к И. Бернулли).

Теорема 6.1 (признак Лейбница). Знакочередующийся ряд (6. 1) сходится, если:

1. Последовательность абсолютных величин членов ряда монотонно убывает, т. е.

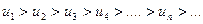
2. Общий член ряда стремится к нулю: .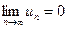

При этом сумма 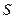ряда (6.1) удовлетворяет неравенствам:

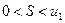. (6.2)

Рассмотрим сначала частичную сумму четного числа (2m) членов ряда (6.1). Имеем

.

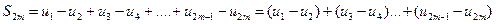Выражение в каждой скобке, согласно первому условию теоремы, положительно. Следовательно, сумма 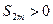и возрастает с возрастанием номера 2m.

С другой стороны, 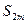можно переписать так:

.

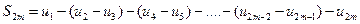Легко видеть, что 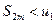. Таким образом, последовательность 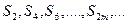, возрастает и ограничена сверху. Следовательно, она имеет предел 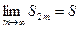, причем .

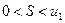Рассмотрим теперь частичные суммы нечетного числа (2m + 1) членов ряда (6.1). Очевидно, что 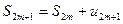. Отсюда следует, что

,

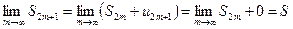т. к. 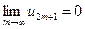в силу второго условия теоремы. Итак, 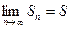как при четном n, так и при нечетном n. Следовательно, ряд (6.1) сходится, причем .

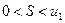Замечания.

1. Исследование знакочередующегося ряда вида

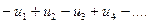(6.3)

(с отрицательным первым членом) сводится путем умножения всех его членов на (-1) к исследованию ряда (6.1).

Ряды (6.1) и (6.3), для которых выполняются условия теоремы Лейбница, называются лейбницевскими (или рядами Лейбница).

2. Соотношение (6.2) позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму S данного ряда его частичной суммой S_n. Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд 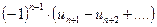, сумма которого по модулю меньше первого члена этого ряда, т. е. 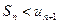. Поэтому ошибка меньше модуля первого из отброшенных членов.

Пример 6.1. Вычислить приблизительно сумму ряда .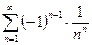

Решение: Данный ряд лейбницевского типа. Он сходится. Можно записать: 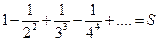. Взяв пять членов, т. е. заменив S на

.

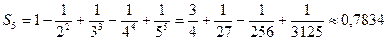сделаем ошибку, меньшую, чем 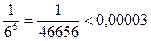. Итак, .

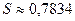Дата добавления: 2015-06-04