Элементы механики жидкости. Колебания

ТЕМА: МЕХАНИКА ТВЁРДОГО ТЕЛА.

КОНТРОЛЬНАЯ РАБОТА № 2

Задача № 1. Сплошной шарик массой 400 г и радиусом 5 см вращается вокруг оси, проходящей через его центр. Закон вращения шара имеет вид: j = 2 + t − 2t². Определить тормозящий момент.

Задача № 2. Диск массой 2 кг радиусом 10 см вращается вокруг горизонтальной оси, проходящей через его центр с частотой 600 мин^-1. Через 20 с под действием тормозящего момента диск остановился. Считая массу диска равномерно распределённой, найти тормозящий момент и число оборотов, которое сделает диск до полной остановки.

Задача № 3. Стержень массой 1 кг и длиной 1 м вращается вокруг оси, проходящей через один из его концов по закону: j = 2 + t + t². Определить момент силы, действующей на другой конец.

Задача № 4. Сплошной диск массой 0,2 кг вращается вокруг оси, проходящей через его центр масс под действием момента сил 0,8×10^-2 Н×м. Закон вращения имеет вид: j = 5 − t + 2t². Определить радиус диска.

Задача № 5. Полый цилиндр вращается относительно оси, совпадающей с осью цилиндра. Закон вращения имеет вид: j = 10 − 5t + 0,5t². Определить момент инерции и массу цилиндра, если его радиус 0,05 м. Момент силы относительно оси вращения, действующий на цилиндр, равен 0,75 Н×м.

Задача № 6. Однородный стержень длиной 1 м и массой 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением вращается стержень, если вращающий момент равен 20×10^-2 Н×м?

Задача № 7. Два шара радиусами по 5 см закреплены на концах тонкого стержня, масса которого значительно меньше массы шаров. Расстояние между центрами шаров 0,5 м. Масса каждого шара 1 кг. Найти: 1) момент инерции этой системы относительно оси, проходящей через середину стержня перпендикулярно его длине, 2) момент инерции этой системы относительно той же оси, считая шары материальными точками, массы которых сосредоточены в их центрах.

Задача № 8. К ободу однородного диска радиусом 0,2 м приложена постоянная касательная сила F = 100 Н. При вращении на диск действует момент сил трения М_тр = 0,5 Н×м. Найти массу диска, если известно, что диск вращается с постоянным угловым ускорением 100 рад/с².

Задача № 9. Однородный диск радиусом 0,4 м и массой 5 кг вращается вокруг оси, проходящей через его центр. Зависимость угловой скорости вращения диска от времени даётся уравнением: w = 4 + 8t. Найти величину касательной силы, приложенной к ободу диска. Трением пренебречь.

Задача № 10. Две гири массой 2 кг и 1 кг соединены нитью и перекинуты через блок. Радиус блока 10 см и его масса 1 кг. Найти: 1) ускорение, с которым движутся гири, 2) натяжения нитей Т₁ и Т₂, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.

Задача № 11. На барабан массой 12 кг намотан шнур, к концу которого привязан груз массой 2 кг. Найти ускорение груза. Барабан считать однородным цилиндром. Трением пренебречь.

Задача № 12. Диск массой 4 кг катится без скольжения по горизонтальной плоскости со скоростью 8 м/с. Найти кинетическую энергию диска.

Задача № 13. Найти линейное ускорение движения центров тяжести: 1) шара, 2) диска, 3) обруча, скатывающихся без скольжения с наклонной плоскости с углом наклона 30⁰.

Задача № 14. Имеются два цилиндра: алюминиевый (сплошной) и свинцовый (полый) – одинакового радиуса 6 см и одинаковой массы 0,5 кг. Найти моменты инерции этих цилиндров. За сколько времени каждый цилиндр скатится без скольжения с наклонной плоскости? Высота наклонной плоскости 0,5 м, угол наклона 30°. Начальная скорость цилиндров равна нулю.

Задача № 15. Горизонтальная платформа массой 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, делая 10 об/мин. Человек массой 60 кг стоит при этом на краю платформы. С какой скоростью начнёт вращаться платформа, если человек перейдёт от края платформы к её центру? Считать платформу круглым однородным диском, а человека – точечной массой.

Задача № 16. Стержень массой 2 кг и длиной 1 м может вращаться вокруг оси, проходящей через его середину перпендикулярно стержню. В конец стержня попадает пуля массой 10 г, летящая перпендикулярно оси и стержню со скоростью 500 м/с. Определить угловую скорость, с которой начнёт вращаться стержень, если пуля застрянет в нём.

Задача № 17. Два горизонтально вращающихся один над другим диска расположены так, что плоскости их параллельны, а центры лежат на одной вертикали. Угловая скорость и момент инерции первого диска равны 10 рад/с и 2×10^-3 кг×м², а второго – соответственно 5 рад/с и 4×10^-3 кг×м². Первый диск падает на второй и система вращается как единое целое. Определить угловую скорость вращающейся системы и изменение кинетической энергии дисков после падения первого на второй.

Задача № 18. Сплошной цилиндр массой 10 кг катится без скольжения с постоянной скоростью 10 м/с. Определить кинетическую энергию цилиндра и время до его остановки, если на него подействует сила 50 Н.

Задача № 19. Полый цилиндр массой 2 кг катится по горизонтальной поверхности со скоростью 20 м/с. Определить силу, которую необходимо приложить к цилиндру, чтобы остановить его на пути 1,6 м?

Задача № 20. Сплошной шар скатывается с наклонной плоскости, длина которой 10 м и угол наклона 30°. Определить скорость шара в конце наклонной плоскости.

Задача № 21. Маховик, имеющий форму диска массой 30 кг и радиусом 10 см, был раскручен до частоты 300 мин^-1. Под действием силы трения диск остановился через 20 с. Найти момент силы трения, считая его постоянным.

Задача № 22. Какой скоростью должен обладать шар, катящийся без скольжения, чтобы подняться по наклонной плоскости, составляющей с горизонтом угол 30°, на высоту 2 м, если сила сопротивления равна 0,2 веса шара? Чему равно время подъёма?

Задача № 23. Сначала диск, а потом обруч скатываются с наклонной плоскости, составляющей угол 30° с горизонтом. Чему равны их ускорения?

Задача № 24. Шар и сплошной цилиндр имеют одинаковую массу по 5 кг и катятся с одинаковой скоростью 10 м/с. Найти кинетические энергии этих тел.

Задача № 25. Шар диаметром 6см катится без скольжения по горизонтальной плоскости, делая 4 об/с. Масса шара 0,25 кг. Найти кинетическую энергию шара.

Задача № 26. Обруч и диск имеют одинаковую массу и катятся без скольжения с одинаковой линейной скоростью. Кинетическая энергия обруча равна 4 Дж. Найти кинетическую энергию диска.

Задача № 27. Шар массой 1 кг, катящийся без скольжения, ударяет о стенку и отскакивает от неё. Скорость шара до удара о стенку v₁ = 10 см/с, после удара v₂ = 8 см/с. Найти количество тепла, выделившееся при ударе.

Задача № 28. Обруч массой 100 г и диаметром 60 см вращается вокруг оси, проходящей через центр, делая 20 об/с. Какую работу надо совершить, чтобы остановить обруч?

Задача № 29. Кинетическая энергия вала, вращающегося с постоянной скоростью, соответствующей 5 об/с, равна 60 Дж. Найти момент количества движения этого вала.

Задача № 30. Колесо, вращаясь равнозамедленно при торможении, уменьшило за 1 мин скорость вращения от 300 до 180 об/мин. Момент инерции колеса равен 2 кг×м². Найти: 1) угловое ускорение колеса, 2) тормозящий момент, 2) работу торможения.

Задача № 31. Однородный стержень совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей через его верхний конец. Длина стержня 0,5 м. Найти период колебаний стержня.

Задача № 32. Обруч диаметром 56,5 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти период этих колебаний.

Задача № 33. В дне цилиндрического сосуда имеется круглое отверстие диаметром d = 1 см. Диаметр сосуда D = 0,5 м. Найти зависимость скорости понижения уровня воды в сосуде от высоты h этого уровня. Найти численное значение этой скорости для высоты h = 0,2 м.

Задача № 34. На столе стоит сосуд с водой, в боковой поверхности которого имеется малое отверстие, расположенное на расстоянии h₁ от дна сосуда и на расстоянии h₂ от уровня воды. Уровень воды в сосуде поддерживается постоянным. На каком расстоянии от отверстия (по горизонтали) струя воды падает на стол? Задачу решить для случая: h₁ = 25 см, h₂ = 16 см.

Задача № 35. Цилиндрический бак высотой h = 1 м наполнен до краёв водой. За какое время вся вода выльется через отверстие, расположенное у дна бака? Площадь поперечного сечения отверстия в 400 раз меньше площади поперечного сечения бака.

Задача № 36. В сосуд льётся вода, причём за 1 с наливается 0,2 л воды. Каков должен быть диаметр отверстия в дне сосуда, чтобы вода в нём держалась на постоянном уровне, равном 8,3 см?

Задача № 37. Шарик всплывает с постоянной скоростью в жидкости, плотность которой в 4 раза больше плотности материала шарика. Во сколько раз сила трения, действующая на всплывающий шарик, больше веса этого шарика?

Задача № 38. Какой наибольшей скорости может достичь дождевая капля диаметром 0,3 мм, если динамическая вязкость воздуха равна 1,2×10^-4 г/см×с?

Задача № 39. Смесь свинцовых дробинок диаметром 3 мм и 1 мм опустили в бак с глицерином глубиной 1 м. Насколько позже упадут на дно дробинки меньшего диаметра по сравнению с дробинками большего диаметра? Плотность глицерина 1300 кг/м³ и динамическая вязкость при температуре опыта 14,7 г/см×с. Остальные данные взять из таблиц.

Задача № 40. Стальной шарик диаметром 1 мм падает с постоянной скоростью 0,185 см/с в большом сосуде, наполненном касторовым маслом. Найти динамическую вязкость касторового масла при температуре опыта. Необходимые данные взять из таблиц.

Задача № 41. Пробковый шарик радиусом 5 мм всплывает в сосуде, наполненном касторовым маслом. Плотность масла принять равной 0,97 г/см³ и плотность пробки 270 кг/м³. Чему равны динамическая и кинематическая вязкости касторового масла в условиях опыта, если шарик всплывает с постоянной скоростью 3,5 см/с?

Задача № 42. В боковую поверхность цилиндрического сосуда радиусом R = 2 см вставлен горизонтальный капилляр внутренним радиусом r = 1 мм и длиной l = 2 см. В сосуд налито касторовое масло, динамическая вязкость которого равна 12 г/см×с. Найти зависимость скорости v понижения уровня касторового масла в цилиндрическом сосуде от высоты h этого уровня над капилляром. Найти численное значение этой скорости при h = 26 см. Плотность касторового масла принять равной 900 кг/м³.

Задача № 43. В боковую поверхность сосуда вставлен горизонтальный капилляр, внутренний радиус которого 1мм и длина 1,5 см. В сосуд налит глицерин, динамическая вязкость которого в условиях опыта равна 1 Н×с/м². Уровень глицерина в сосуде поддерживается постоянным на высоте 0,18 м выше капилляра. Сколько времени потребуется на то, чтобы из капилляра вытекло 5 см³ глицерина?

Задача № 44. В бочку заливается вода со скоростью 400 см³/с. На дне бочки образовалось отверстие площадью поперечного сечения 0,64 см². Пренебрегая вязкостью воды, определите уровень воды в бочке.

Задача № 45. В дне сосуда имеется отверстие диаметром d₁. В сосуде вода поддерживается на постоянном уровне, равном h. Считая, что струя не разбрызгивается и пренебрегая силами трения в жидкости, определите диаметр струи, вытекающей из сосуда на расстоянии h₁ = 3h от его дна.

Задача № 46. Определите, на какую высоту поднимается вода в вертикальной трубке, впаянной в узкую часть горизонтальной трубы диаметром d₂ = 4 см, если в широкой части трубы диаметром d₁ = 16 см скорость воды v₁ = 30 см/с.

Задача № 47. При какой относительной скорости движения релятивистское сокращение длины движущегося тела составляет 25%?

Задача № 48. Какую скорость должно иметь движущееся тело, чтобы его продольные размеры уменьшились в два раза?

Задача № 49. Мезоны космических лучей достигают поверхности Земли с самыми разнообразными скоростями. Найти релятивистское сокращение размеров мезона, имеющего скорость, равную 95% скорости света.

Задача № 50. Как увеличится масса a-частицы при ускорении её от начальной скорости, равной нулю, до скорости, равной 0,9 скорости света?

Задача № 51. До какой энергии можно ускорить частицы в циклотроне, если относительное увеличение массы частицы не должно превышать 5%? Задачу решить для электронов и для протонов.

Задача № 52. Найти скорость мезона, если его полная энергия в 10 раз больше энергии покоя.

Задача № 53. Какую долю скорости света должна составлять скорость частицы, чтобы её кинетическая энергия была равна её энергии покоя?

Задача № 54. Синхрофазотрон даёт пучок протонов с кинетической энергией 10 000 МэВ. Какую долю скорости света составляет скорость протонов в этом пучке?

Задача № 55. Электроны, вылетающие из циклотрона, обладают кинетической энергией 0,67 МэВ. Какую долю скорости света составляет скорость этих электронов?

Задача № 56. Масса движущегося электрона вдвое больше его массы покоя. Найти кинетическую энергию этого электрона.

Задача № 57. Какую скорость должно иметь движущееся тело, чтобы его продольные размеры уменьшились в два раза?

Задача № 58. При какой относительной скорости движения релятивистское сокращение длины движущегося тела составит 50%?

Задача № 59. Протон движется со скоростью 0,75 скорости света. Найти количество движения и кинетическую энергию протона.

Задача № 60. Радиоактивное ядро, вылетевшее из ускорителя со скоростью 0,4 скорости света, выбросило в направлении своего движения b-частицу со скоростью 0,75 скорости света относительно ускорителя. Найти скорость частицы относительно ядра.

Задача № 61. Электрон, скорость которого 0,97 скорости света, движется навстречу протону, имеющему скорость 0,5 скорости света. Определить скорость их относительного движения.

Задача № 62. Две частицы движутся навстречу друг другу со скоростями 0,9 скорости света. Определить скорость их относительного движения.

Задача № 63. Найти собственное время жизни нестабильной частицы m-мезона, движущегося со скоростью 0,99 скорости света, если расстояние, пролетаемое им до распада, равно примерно 10 км.

Задача № 64. Электрон, скорость которого равна 0,7 скорости света, движется навстречу протону, имеющему скорость 0,6 скорости света. Определить скорость их относительного движения.

Задача № 65. Две частицы движутся навстречу друг другу со скоростями, равными 0,8 скорости света. Определить скорость их относительного движения.

Задача № 66. Написать уравнение гармонического колебательного движения с амплитудой 0,1 м, периодом 4 с и начальной фазой, равной 0.

Задача № 67. Амплитуда гармонических колебаний равна 50 мм, период − 4 с, начальная фаза равна π/4. 1) Написать уравнение этого колебания. 2) Найти смещение колеблющейся точки от положения равновесия при t = 0 и при t = 1, 5 с. 3) Начертить график этого движения.

Задача № 68. Написать уравнение гармонического колебатель­ного движения, если начальная фаза колебания равна: 1) 0, 2) π, 3) π/2, 4) 3π/2, 5) 2π. Амплитуда колебаний 5 см и период колебаний 8 с. Начертить график колебаний во всех этих случаях.

Задача № 69. Уравнение движения точки дано в виде: 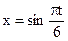. Найти моменты времени, в которые достигаются максимальная скорость и максимальное ускорение.

Задача № 70. Написать уравнение гармонического колебания, если максимальное ускорение точки 49,3 см/с², период колебаний 2 с и смещение точки от положения равновесия в начальный момент времени 25 мм.

Задача № 71. Начальная фаза гармонического колебания равна 0. При смещении точки от положения равновесия, равном 2,4 см, скорость точки равна 3 см/с, а при смещении, равном 2,8 см, скорость равна 2 см/с. Найти амплитуду и период этого колебания.

Задача № 72. Материальная точка массой 10 г колеблется по уравнению: 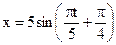см. Найти максимальную силу, действующую на точку и полную энергию колеблющейся точки.

Задача № 73. К пружине прикреплён груз весом 10 Н. Зная, что пружина под действием силы 1 Н растягивается на 1,5 см, определить период вертикальных колебаний груза.

Задача № 74. К пружине подвешен груз. Зная, что максимальная кинетическая энергия колебаний груза равна 1 Дж, найти коэффициент деформации пружины. Амплитуда колебаний 5 см.

Задача № 75. К пружине подвешена чашка весов с гирями. При этом период вертикальных колебаний равен 0,5 с. После того как на чашку весов положили ещё добавочные гири, период вертикальных колебаний стал равен 0,6 с. Насколько удлинилась пружина от прибавления этого добавочного груза?

Задача № 76. К резине длиной 40 см и радиусом 1 мм подвешена гиря весом 0,5 Н. Зная, что модуль Юнга этой пружины равен 0,3 Н/мм, найти период вертикальных колебаний гири.

Указание: Учесть, что коэффициент деформации k резины связан с модулем Юнга Е резины соотношением: 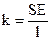, где S − площадь поперечного сечения резины и l − её длина.

Задача № 77. Найти амплитуду и начальную фазу гармони­ческого колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями:

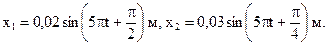
Задача № 78. 1) Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнения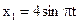ми: см и 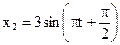см. 2) Написать уравнение результирующего колебания.

Задача № 79. Амплитуда затухающих колебаний математического маятника за 1 минуту уменьшилась вдвое. Во сколько раз она уменьшилась за 2 минуты?

Задача № 80. Уравнение незатухающих колебаний дано в виде: 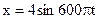см. Найти смещение от положения равновесия точки, находящейся на расстоянии 75 см от источника колебаний, через 0,01 с после начала колебаний. Скорость распространения колебаний 300 м/с.

Дата добавления: 2015-06-04