Примеры решения задач

1. В сосуде объёмом 3 м³ находится смесь 7 кг азота и 2 кг водорода при температуре 27°С. Определить давление и молярную массу смеси газов.

Дано: V = 3 м³; m₁ = 7 кг; m₂ = 2 кг; μ₁ = 28×10^-3 кг/моль;
μ₂ = 2×10^-3 кг/моль; Т = 300 К.

Найти: р, μ.

Решение: Воспользуемся уравнением Менделеева-Клапей­рона, применив его к азоту и водороду:

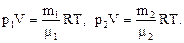
(1)

В этих уравнениях р₁, р₂ – парциальные давления азота и водорода, μ₁, μ₂ – молярные массы азота и водорода,

R = 8,31 Дж/моль×К – универсальная газовая постоянная. По закону Дальтона,

р = р1+ р2.

(2)

Из уравнений (1) выразим р₁ и р₂ и подставим в (2):

(3)

С другой стороны,

(4)

Сравнивая выражения (3) и (4), получим:

откуда

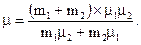
(5)

Подставляя в выражение (5) числовые данные, получим:

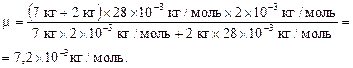
Подставляя числовые данные в выражение (4), получим:

Ответ: 1,04 МПа; 7,2×10^-3 кг/моль.

2. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 4 кг кислорода при температуре 200 К?

Дано: m = 4 кг; Т = 200 К; μ = 32×10^-3 кг/моль.

Найти: <Е_пост>, <Е_вращ>.

Решение: Считаем кислород идеальным газом. Молекула кислорода двухатомная, связь между атомами считаем жёсткой, тогда число степеней свободы молекулы кислорода равно 5. в среднем на одну степень свободы приходится энергия 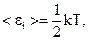где k − постоянная Больцмана. Поступательному движению приписывается три, а вращательному две степени свободы. Тогда энергия одной молекулы равна:

<ε_вращ> = kT.

Число молекул, содержащихся в массе газа:

где N_А – число Авогадро. Тогда средняя кинетическая энергия поступательного движения молекул кислорода равна:

(1)

где R = N_A × k.

Средняя кинетическая энергия вращательного движения молекул кислорода равна:

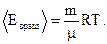
(2)

Подставляя числовые значения в формулы (1) и (2), имеем:

Ответ: 3,12×10⁵ Дж; 2,08×10⁵ Дж.

3. Определить среднюю длину свободного пробега молекул и число соударений за 1 с, происходящих между всеми молекулами водорода, находящегося в сосуде ёмкостью 1 л при температуре 27°С и давлении 10 кПа.

Дано: V = 1 л = 1×10^{-3 м3}; μ = 2×10^-3 кг/моль; Т = 300 К;
р = 1×10⁴ Па; d = 2,3×10^{-10 м.}

Найти: <λ>, Z.

Решение: Средняя длина свободного пробега молекул водорода равна:

(1)

где d − эффективный диаметр молекулы водорода, n – концентрация молекул, которую можно определить из уравнения

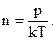
(2)

Подставляя (2) в (1), имеем:

(3)

Число соударений Z, происходящих между всеми молекулами за 1 с, равно:

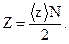
(4)

В формуле (4) <z> − среднее число соударений одной молекулы за 1 с, N − число молекул водорода в сосуде объёмом 1 л. Число молекул в сосуде

N = n × V.

(5)

Среднее число соударений молекулы за 1 с равно:

(6)

где <v> − средняя арифметическая скорость молекулы.

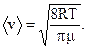
(7)

Подставляя в (4) выражения (5), (6) и (7), находим:

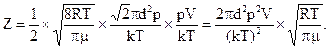
Подставляя числовые данные, получим:

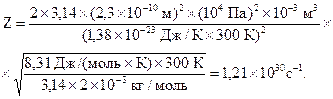
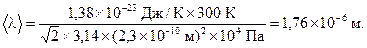
Ответ: 1,76×10^{-6 м; 1,21×1030} с^-1.

4. Определить коэффициенты диффузии и внутреннего трения гелия, находящегося при температуре 200 К и давлении 10⁴ Па.

Дано: μ = 4×10^-3 кг/моль; Т= 200 К; р = 10⁴ Па; d = 1,9×10^{-10 м.}

Найти: D, η.

Решение: Коэффициент диффузии находят по формуле:

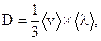
(1)

где <v> − средняя арифметическая скорость молекул, равная:

(2)

<λ> − средняя длина свободного пробега молекул.

Для нахождения <λ> воспользуемся формулой, взятой из решения примера 3:

(3)

Подставляя (2) и (3) в (1), получим:

(4)

Коэффициент внутреннего трения равен:

(5)

Здесь ρ – плотность газа при данных условиях.

Для нахождения ρ воспользуемся уравнением состояния идеального газа (уравнением Менделеева-Клапейрона):

(6)

Учитывая, что имеем:

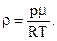
(7)

Коэффициент внутреннего трения газа может быть выражен через коэффициент диффузии:

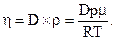
(8)

Подставляя числовые значения в формулы (4) и (8), получаем:

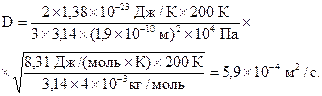
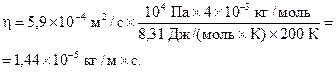
Ответ: 5,9×10^-4 м²/с; 1,44×10^-5 кг/м×с.

5. Кислород массой 320 г нагревают при постоянном давлении от 300 до 310 К. определить количество теплоты, поглощённой газом; изменение внутренней энергии и работу расширения газа.

Дано: m = 320 г = 0,32 кг; Т₁ = 300 К; Т₂ = 310 К; μ = 32×10^-3 кг/моль.

Найти: Q, ΔU, A.

Решение: Количество теплоты, необходимое для нагревания газа при постоянном давлении, равно:

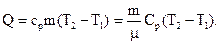
(1)

Здесь c_p, C_p – удельная и молярная теплоёмкости газа при постоянном давлении. Для всех двухатомных газов с жёсткой связью ,

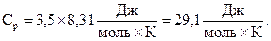
Изменение внутренней энергии газа равно:

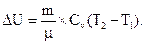
(2)

Здесь C_v –молярная теплоёмкость газа при постоянном объёме. Для всех двухатомных газов с жёсткой связью

.

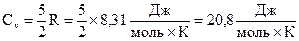Работа расширения газа при изобарном процессе: А= p×ΔV, где ΔV= V₂ – V₁ – изменение объёма газа, который можно найти из уравнения Менделеева – Клапейрона:

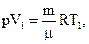
(3)

(4)

Вычитанием выражения (4) из выражения (3) находим:

следовательно,

(5)

Подставляя числовые данные в формулы (1), (2) и (5), получим:

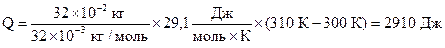
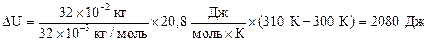
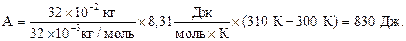
Ответ: 2910 Дж; 2080 Дж; 830 Дж.

6. Объём аргона, находящегося при давлении 80 кПа, увеличился от 1 до 2 л. Насколько изменится внутренняя энергия газа, если расширение производилось: а) изобарно; б) адиабатно?

Дано: V₁= 1 л = 10^{-3 м3}; V₂= 2 л = 2×10^{-3 м3}; р = 0,8×10⁵ Па;
μ = 40×10^-3 кг/моль.

Найти: ΔU.

Решение: Применим первый закон термодинамики. Согласно этому закону, количество теплоты Q, переданное системе, расходуется на увеличение внутренней энергии ΔU и на внешнюю механическую работу А:

Q = ΔU + A.

(1)

Здесь

	(2)
	(3)

где i – число степеней свободы.

Тогда выражение (2) примет вид:

(4)

Запишем уравнение Менделеева – Клапейрона для начального и конечного состояний газа при изобарном процессе:

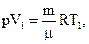
Имеем после вычитания:

(5)

Подставив (5) в (4), получим:

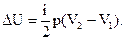
(6)

При адиабатном расширении газа теплообмена с внешней средой не происходит, поэтому Q = 0. Уравнение (1) запишем в виде:

ΔU + A = 0.

(7)

Это соотношение устанавливает, что работа расширения газа может быть произведена только за счёт уменьшения внутренней энергии газа (знак минус перед ΔU):

A = −ΔU.

(8)

Работа, совершённая газом при адиабатном процессе, равна:

(9)

Здесь γ = Сp/Cv = (i+2)/i − показатель степени адиабаты. Для аргона (одноатомного газа) i = 3, имеем: γ = 1,67.

Найдём изменение внутренней энергии при адиабатном процессе для аргона, учитывая формулы (8) и (9):

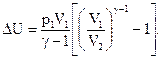
(10)

Подставляя числовые значения в (6) и (10), получаем:

а) при изобарном расширении

б) при адиабатном расширении

Ответ: 120 Дж; − 44,6 Дж.

7. Температура нагревателя тепловой машины 450 К. Температура холодильника 300 К. Определить КПД тепловой машины, работающей по циклу Карно и полную мощность машины, если нагреватель ежесекундно передаёт ей 1525 Дж теплоты.

Дано: Т₁ = 450 К, Т₂ = 300 К, Q = 1525 Дж, t = 1 с.

Найти: η; N.

Решение: КПД машины равен:

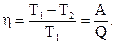
(1)

Из выражения (1) находим:

.

Произведём вычисления:

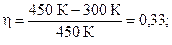
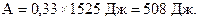
Эта работа совершается за 1 с, следовательно, полная мощность машины равна:

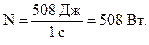
Ответ: 0,33; 508 Вт.

8. Горячая вода некоторой массы отдаёт теплоту холодной воде такой же массы, и температуры их становятся одинаковыми. Показать, что энтропия при этом увеличивается.

Дано: Т₁ – температура горячей воды, Т₂ – температура холодной воды, θ − температура смеси. Показать, что: ΔS > 0.

Решение: Температуру смеси определим из уравнения теплового баланса:

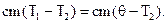
Отсюда

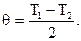
(1)

Изменение энтропии, происходящее при охлаждении горячей воды:

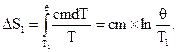
Изменение энтропии, происходящее при нагревании холодной воды:

Изменение энтропии системы:

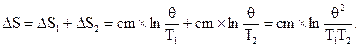
С учётом соотношения (1) имеем:

Так как то ΔS>0.

Дата добавления: 2015-06-04