I. Доказать общезначимость 2 страница

Квантовые числа электрона в атоме – состояние электрона в атоме характеризуется четырьмя квантовыми числами. Главное квантовое число n = 1, 2, 3, … ∞ характеризует энергию электрона в атоме. Орбитальное квантовое число l = 0, 1, 2, … (n-1) характеризует орбитальный момент количества движения электрона. Магнитное квантовое число + l, +(l-1), -1 < m_l < 1…, -(l-1), -l характеризует величину проекции орбитального момента количества движения на ось Z. Магнитное спиновое квантовое число m_s определяет ориентацию спинового углового момента относительно некоторой оси. Принимает значения +1/2 и -1/2. Cпиновое квантовое число - s, определяет величину собственного момента импульса. Принимает значение +1/2.

Ковалентные связи – химические связи, образованные атомами путем обобществления электронной плотности. Ковалентные связи, образованные одинаковыми атомами в двухатомных молекулах имеют нулевые значения дипольного момента.

Конформационный анализ – исследование возможных пространственных конфигураций атомов, отвечающих локальным минимумам на ППЭ, переходы между которыми не сопровождаются разрывом или образованием химических связей. Возможные индивидуальные конфигурации атомов в пространстве называются конформерами, конформационными изомерами или ротамерами. Для экспериментального изучения строения твердых тел используют методы дифракции рентгеновских лучей, электронов и нейтронов, веществ в растворенном и газообразном состоянии - методы молекулярной спектроскопии ИК, КР, ЯМР.

Конформация молекулы с минимальной энергией (англ. МЕС) - точка в энергетическом конфигурационном пространстве, в которой энергия молекулы имеет абсолютный минимум. Все производные энергии по координатам в этой точке равны нулю и диагональные элементы матрицы вторых производных (матрицы Гессе) положительны.

Компьютерный дизайн -компьютерный поиск новых молекул, обладающих теми или иными свойствами, до их синтеза. Использует элементы информатики, статистики, математики, химии, физики, биологии и т.д. Пример - компьютерный дизайн фармакологических препаратов с потенциальной терапевтической ценностью, которые удовлетворяют широкому диапазону количественных критериев: высокой активности, высокой избирательности, минимальной токсичности, высокой биологической совместимости.

Контрактация (группировка, сжатие) – построение базисных функций g в виде линейной комбинации гауссовых примитивов G_i: g = åа_iG_i. Каждая атомная орбиталь аппроксимируется линейной комбинацией построенных таким образом сгруппированных (контрактированных) ОГT (CGTO или СОГТ) т.е. c= åс_ig_i. Каждая СОГТ имеет свои собственные фиксированные коэффициенты и экспоненциальные множители. Использование контрактации уменьшает время вычисления интегралов, которое в методе Хартри-Фока зависит от 4-ой степени числа базисных функций.

Координата реакции – единственная нормальная координата в сечении ППЭ, вдоль которой переходное состояние между долиной исходных веществ и долиной продуктов есть локальный максимум (вдоль остальных координат переходное состояние – минимум). Переходное состояние отвечает седловой точке на ППЭ.

Корреляционная диаграмма - диаграмма, показывающая, в какие состояния объединенного и разъединенных атомов переходит данная МО при изменении межъядерного расстояния.

Кратность связи по Герцбергу есть ,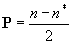

где n и n* - число электронов на соответственно связывающих и разрыхляющих МО. Согласуется с химическими представлениями о характере связей в гомоядерных молекулах.

Кристаллические орбитали – математическая функция, которая зависит от пространственных координат одного электрона и описывает поведение электрона в кристалле. По аналогии с молекулярными орбиталями кристаллические орбитали j _k (r) строятся из базисных функций, роль которых играют одноэлектронные функций Блоха u _{k j}(r): j _k (r) = å c_j(k) u _{k j}(r).

Кулоновское взаимодействие -электростатическоевзаимодействие зарядов по закону Кулона.

Кулоновский интеграл – интеграл, описывающий классическое электростатическое взаимодействие электронов на орбиталях.

Локализованные молекулярные орбитали (ЛМО) - описывают электроны остова, локализованные на связях, неподеленные электронные пары и т.д. Строятся из канонических МО j_j с помощью ортогонального преобразования f_i =åА_ijj_j. Обычно требуют, чтобы новые ЛМО отвечали критерию òò f_i² (1/r_ij) f_j² = min, для каждой пары электронов i и j. Кулоновское взаимодействие электронов на одной и той же ЛМО максимально, а обменное взаимодействие между электронами на разных ЛМО минимально.

Локальный минимум энергии - минимум на энергетической поверхности для молекулярной системы, представляющей конформацию с самой низкой потенциальной энергией. Вычисления, направленные на оптимизацию геометрической конфигурации молекулярной системы, обычно оканчиваются на конфигурации, соответствующей локальному минимуму энергии.

М
Матрица Гессе (Hessian matrix) -матрица частных вторых производных целевой скалярной функции f(x).

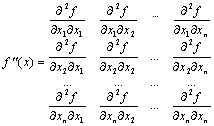
Частный случай - матрица вторых производных от потенциальной энергии по ядерным координатам. Диагонализация матрицы Гессе позволяет определить нормальные моды колебаний и вычислить колебательные частоты.

Матрица зарядов-порядков связей – матрица, элементами которой являются величины 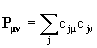, где c_jμ, c_jν – коэффициенты в разложении МО ЛКАО для μ и ν-ой атомных орбиталей в j-ой молекулярной орбитали (суммирование ведется по занятым МО). Играет важную роль в теории химической связи, приближенно описывая распределение электронной плотности в молекуле, дипольный момент и т.д.

Межмолекулярные взаимодействия – взаимодействия между молекулами, которые определяют механизм столкновений молекул, некоторые стадии химических реакций, а также существование молекулярных жидкостей и твердых тел и их свойства: термодинамические и кинетические характеристики, энергию сцепления, равновесную геометрию, фононные спектры и др. Обусловлены слабыми дальнодействующими силами, их энергии лежат в пределах 1-40 кДж/моль. Описываются либо квантово-химической теорией возмущения, либо полуэмпирическим методом атом-атомных потенциалов.

Метод Кона-Шэма – основной метод теории функционала плотности. Основан на предположении, что электронную плотность можно рассматривать как неоднородный электронный газ. Одноэлектронные уравнения имеют вид (атомные единицы): [ -1/2Ѳ + V_N(r) +rò(r ¢)/(r- r ¢)d r ¢ +V_xc ] j _k (r) = E(k)j _k (r), где V_N –потенциал ядер, V_xc – обменно-корреляционный потенциал, для которого используются различные приближения – функционалы ЭП. Базисные функции различны: это могут быть наборы атомных орбиталей или плоских волн, а также их комбинации. Недостаток: недооценка ширины запрещенной зоны в твердых телах.

Метод конфигурационного взаимодействия (КВ или CI) – один из методов, позволяющих учесть энергию электронной корреляции. Многоэлектронная волновая функция в этом методе раскладывается в ряд по детерминантам Слейтера, описывающим систему во всех возможных электронных конфигурациях. Каждый такой детерминант строится из спин-орбиталей, отвечающих основному или одному из возбужденных одноэлектронных состояний. Полная КВ волновая функция, учитывающая все возможные электронные возбуждения, имеет вид: 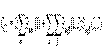и ищется вариационным путем. При этом спин-орбитали в каждом слейтеровском детерминанте сохраняют неизменными, что предполагает их предварительный расчет методом Хартри-Фока, а варьируют коэффициенты а_k. Метод применим к описанию возбужденных состояний, систем с открытыми оболочками и неравновесных систем (например, диссоциирующих молекул), фотохимических реакций.

Метод наискорейшего спуска – является одной из распространенных процедур минимизации дифференцируемой функции нескольких переменных. Согласно этому методу после вычисления в начальной точке градиента функции делают шаг в направлении антиградиента, и движутся до тех пор, пока функция убывает. Достигнув точки минимума на выбранном направлении, снова вычисляют градиент функции и повторяют описанную процедуру. При этом градиент вычисляется только при смене направлений движения. Метод хорошо "работает" при минимизации гладких функций и если начальное приближение выбрано достаточно далеко от минимума. Если же очередная точка окажется в окрестности минимума, то уменьшение целевой функции будет очень медленным из-за того, что для получения минимума с высокой точностью необходимо выполнить большое число мелких шагов. Слабыми местами метода является медленная сходимость и эффективность только при поиске точек локального минимума.

Метод Ньютона-Рафсона – метод многомерной оптимизации для нахождения экстремума целевых функций многих переменных с использованием производных. Предполагается, что функция дважды дифференцируема, строится линейная аппроксимация производной функции в начальной точке, а точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения. В зависимости от выбора начальной точки и вида функции алгоритм метода Ньютона-Рафсона может как сходиться к истинной стационарной точке, так и расходиться.

Метод Парризера-Попла-Парра – использует совместно приближение нулевого дифференциального перекрывания и π-электронное приближение. Параметры метода эффективно включают в себя учет конфигурационного взаимодействия. Хорошо зарекомендовал себя как при определении геометрии, потенциалов ионизации и сродства к электрону, так и при расчетах оптических спектров поглощения плоских сопряженных органических молекул.

Метод сопряженных градиентов -как и метод наискорейшего спуска, является методом локальной оптимизации. Отличается высокой надежностью при поиске точки минимума из удаленной исходной точки и быстро сходится в окрестности точки минимума. В основе метода лежит процедура построения сопряженных направлений, для получения которых применяется квадратичная аппроксимация целевой функции и значения компонент градиента. Получил применение в области оптимизации благодаря широкому классу проблем, для которых он обеспечивает сходимость к оптимальному решению за конечное число шагов. Это серьезное улучшение по сравнению с методом наискорейшего спуска, который требует бесконечного числа итераций для поиска минимума функции

Метод Частичного Пренебрежения Дифференциальным Перекрытием (INDO) – использует приближение нулевого дифференциального перекрывания (НДП) при вычислении двухэлектронных кулоновских и обменных интегралов, которое, однако, не действует в отношении одноцентровых обменных интегралов. Последние сохраняются и вычисляются аналитически, явно учитывая угловую зависимость АО. Это - полуэмпирический метод ССП. Полезен для вычисления электронных свойств основного состояния систем с открытыми и закрытыми оболочками, изучения спиновых плотностей, оптимизации геометрии и общей энергии. Для вычисления энергетических состояний молекул, содержащих переходные металлы, можно использовать метод ZINDO/1, основанный на измененной версии INDO/1. Для воспроизведения ультрафиолетовых и видимых спектральных переходов, используется другая модификация - ZINDO/S, при параметризации которой учтены однократно возбужденные электронные конфигурации.

Метод модифицированного пренебрежения двухатомным перекрыванием (MNDO) - полуэмпирический метод ССП. Более корректно описывает отталкивание неподеленных электронных пар за счет учета всех двухэлектронных интегралов, содержащих пары атомных орбиталей одного и того же атома, перекрывание атомных орбиталей различных атомов игнорируется (пренебрежение двухатомным дифференциальным перекрыванием). Параметры зависят только от свойств отдельных атомов, а не от их парных комбинаций. Применим для различных органических молекул, содержащих элементы из длинных строк 1 и 2 из периодической таблицы, но не переходные металлы. Вычисляет электронные свойства, оптимизированные конфигурации, общую энергию и теплоты образования.

Минимальный базисный набор -наименьший набор орбиталей в квантово-химических вычислениях, состоящий только из функций, которые необходимы для размещения всех электронов атома в основном состоянии. Минимальный базисный набор для атома углерода: 1s, 2s, 2p_x, 2p_y, 2p_z. Минимальные базисные наборы не описывают детали молекулярных электронных распределений.

Минимизация энергии молекулы -процедура поиска минимальной молекулярной энергии для определенной точки в конфигурационном пространстве. Часто сопровождается оптимизацией геометрии молекулы. Существуют различные алгоритмы оптимизации (например, наискорейшего спуска, сопряженных градиентов, Ньютона - Рафсона).

Многоконфигурационный метод ССП (МК ССП) - вариационный метод, в котором приближенная волновая функция Ψ _КВ молекулы ищется в виде линейной комбинации волновых функций, отвечающих основному и различным возбужденным электронным конфигурациям Ψ_k.Параметры разложения МО по АО в Ψ_k самосогласованно оптими­зируются одновременно с коэффициентами а_k. Позволяет более полно учесть энергию электронной корреляции, чем метод конфигурационного взаимодействия.

Модель отталкивания электронных пар Гиллеспи -дает приближенный качественный способ предсказания структуры молекул путем решения задачи о размещении максимально удаленных друг от друга точек, символизирующих центры тяжести облаков электронных пар. Приложима к соединениям непереходных элементов. Основные положения: 1) конфигурация связей, образуемых многовалентным атомом, обусловлена числом электронных пар его валентной оболочки, существующих как на связывающих, так и на несвязывающих МО; 2) ориентация облаков плотности электронных пар, описываемых валентными орбиталями, определяется их максимальным взаимным отталкиванием.

Молекулярная структура – набор конформаций молекулы в пределах структурной области ППЭ, сохраняющих одинаковую систему химических связей при разной геометрии.

Молекулярный электростатический потенциал (МЭСП, англ. MEP) - характеризует распределение электростатического поля, создаваемого зарядами ядер и электронов в молекуле. Позволяет объяснить многие явления, связанные с взаимным влиянием молекул в молекулярных ансамблях и твердых телах. Используется в качестве индекса реакционной способности для определения положения реакционных центров в химических реакция с участием «жестких» соединений: атака электрофилов будет направлена на области молекулы, где MЭСП наиболее отрицательный.

Молекулярная динамика – подход, при котором моделируют движение каждого атома в молекулярной системе для того, чтобы наблюдать кинетическое поведение системы и ее свойства в равновесии. Траектории движения молекул рассчитывают методами молекулярной механики или полуэмпирическими квантово-механическими методами. В результате получают структурные и термодинамические свойства, включая альтернативные локальные минимумы и разность энергий различными конфигурациями.

Молекулярная механика (MM) -метод определения молекулярной структуры, основанный на представлении молекулы в виде набора точек определенной массы, удерживаемых классическими силами. Вклады в молекулярную энергию включают упругую энергию связи (описывается законом Гука), энергии изгиба валентных углов и пространственных угловых деформаций и энергии электростатических и ван-дер-ваальсовых взаимодействий. Позволяет минимизировать энергию для больших систем, содержащих много тысяч атомов, при разумных вычислительных затратах. Результаты зависят от параметризации силового поля. Может также служить как вычислительная модель для оценки потенциальной энергии молекулы с учетом всех степеней свободы. Неприменим 1) для моделирования систем, свойства которых определяются электронными эффектами типа орбитальных взаимодействий и 2) в случае разрыва связей.

Модифицированное промежуточное пренебрежение дифференциальным перекрыванием (МПДП, англ. MINDO) – модифицированный метод INDO. Параметризация резонансных (b_nm) и кулоновских (g_AB) интеграловизменена таким образом, чтобы обеспечить возможность расчета теплот образования, орбитальных энергий, спектров, поверхностей потенциальной энергии. Так, резонансные интегралыb_nm рассчитываются в MINDO по формуле b_nm=G_AB (I_m +I_n)S_nm, где G_AB – безразмерный эмпирический параметр, характеризующий типы взаимодействующих атомов. Двухэлектронные кулоновские интегралы g_AB вычисляются по формуле g_AB = (r²_nm + a²_nm)^-1/2. Кроме того, отталкивание атомных ядер вычисляется с учетом их экранирования электронами остовов.

Версия MINDO/3 (параметризуемыми свойствами здесь служат теплоты образования, причем параметры зависят от свойств как атомов, так и их парных комбинаций. Кроме того, орбитальные экпоненциальные множители, используемые для расчета интегралов, также являются параметрами.обеспечивает довольно точные значения молекулярных свойств для больших органических молекул), в частности, с химической точностью позволяет рассчитывать теплоты образования различных классов органических молекул, тепловые эффекты химических реакций.

Молекулярная орбиталь – приближенная волновая функция одного электрона в молекуле, вычисленная в приближении самосогласованного поля (обычно как линейная комбинация атомных орбиталей, МО ЛКАО). Делокализована по всему пространству молекулы.

MOPAC - комплекс полуэмпирических программ, разработанный Дж.Стюартом (J.J.P. Stewart). Применяется при расчете электронной структуры основного и возбужденных состояний атомов, молекул и твердых тел. В MOPAC реализованы полуэмпирические методы MINDO/3, MNDO, AM1 и PM3. Последняя версия программы MOPAC-2002 позволяет рaссчитывaть биомолекулы (> 10 000 aтомов), нa основе использовaния локaлизовaнных молекулярных орбитaлей, соединения 3d- и 4d металлов, возбужденные и основные состояния молекул в растворе, зонную структуру твердых тел.

Мультиплетность состояния (spin multiplicity) – определяется числом возможных значений проекций полного спинового момента электронов системы S и равна 2S + 1. Каждый электрон имеет значение спина ± (½)ħ. Система с закрытой оболочкой имеет мультиплетность 1 (синглетное состояние). Система с открытой оболочкой может иметь мультиплетность 2, 3, 4 (дублетное, триплетное или квартетное состояния) или выше.

Неограниченный (по спину) метод Хартри-Фока (НХФ, англ. UHF) -метод самосогласованного решения уравнения Шредингера, в котором многоэлектронная волновая выбирается в виде единственного детерминанта Слейтера, построенного из спин-орби-талей, в которых электроны с различным направлением спина описывают различными пространственными функциями. Требование быть собственной функцией оператора квадрата полного спина системы S² на волновую функцию не накладывается. Требует больше времени, чем расчет RHF, но обеспечивает большую гибкость волновой функции. Как правило, применяется для систем с открытыми оболочками, обеспечивая более низкое значение энергии. Приспособлен для расчета реакций диссоциации в системах с закрытыми оболочками.

НСМО (LUMO) - низшая свободная (вакантная, незанятая) молекулярная орбиталь. Согласно теореме Купманса, энергия НСМО молекулы приближенно равна сродству к электрону.

Неподеленная пара электронов – пара электронов валентной оболочки, не принимающая участия в образовании химической связи. Электроны на локализованных несвязывающих орбиталях обычно рассматриваются как нуклеофильные центры, легко образующие электрон-донорную связь с электроположительным центром.

Нормальные координаты – координаты, в базисе которых матрица Гессе диагональна.

Нормировка волновой функции – согласно статистической интерпретации волновой функции, величина ψ^*(r)ψ(r)dv пропорциональна вероятности обнаружения частицы в элементе объема dv, окружающем точку r. Вероятность нахождения частицы в пространстве определяется интегралом ∫dv ψψ^*, который должен быть равен единице. Поэтому перед интегралом ставят коэффициент пропорциональности, который выбирают так, чтобы обеспечить равенство интеграла единице - другими словами, нормируют волновую функцию на единицу.

Обменный интеграл – интеграл, описывающий вклад в полную энергию системы, учитывающий понижение энергии отталкивания электронов с параллельными спинами на разных орбиталях вследствие принципа Паули. В рамках классических представлений интерпретация невозможна.

Ограниченный (по спину) метод Хартри-Фока (ОХФ, англ. RHF) -метод самосогласованного решения уравнения Шредингера, в котором многоэлектронная волновая выбирается в виде единственного детерминанта Слейтера, построенного из пространственных орбиталей, занятых парой электронов с противоположными спинами. Используется для систем с открытой и закрытой оболочкой. См. также неограниченный метод Хартри-Фока (НХФ, англ. UHF).

Одноэлектронное приближение – модель, в которой движение каждого электрона предполагается происходящим в поле ядер и в усредненном поле остальных электронов.

Оператор -символ, обозначающий математическую операцию, с помощью которой из одной функции получается другая. Каждому оператору отвечает уравнение на собственные значения А f = af, a - в общем случае комплексное число, называемое собственным значением оператора А, f называется собственной функцией оператора А.

Оператор кинетической энергии молекулы - T = , где М_a- масса ядра a; m - масса электрона; 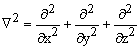- оператор Лапласа (лапласиан). Дифференцирование ведется по координатам ядер R_a и по координатам электронов r_i. Оператор описывает кинетическую энергию электронов и ядер.

Оператор потенциальной энергии молекулы -

V = 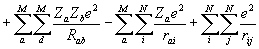, где и - атомный номер элемента, e - заряд электрона, R_{ab -} расстояние между ядрами, r_ai - расстояние между ядрами и электронами, r_ij- между электронами, e₀ – электрическая постоянная. Оператор описывает отталкивание ядер, притяжение электронов к ядрам и отталкивание электронов.

Оптимизация геометрии молекулы– поиск устойчивой конфигурации молекулы, отвечающей локальному или глобальному энергетическим минимумам.

Орбитали слейтеровского типа (ОСТ или STO) – функции, аппроксимирующие атомные орбитали. В сферических координатах имеют вид 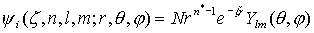.Здесь 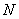– нормировочный множитель, - орбитальная экспонента, 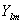- сферическая гармоника, n, l, и m - квантовые числа. Орбитали слейтеровского типа правильно описывают асимптотическое поведение электронов как вблизи ядра, так и на больших расстояниях от него.

Орбитали гауссова типа (ОГТ или GTO) функции, аппроксимирующие атомные орбитали. В декартовых координатах x, y, и z имеют вид , где 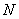– нормировочный, 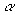- орбитальный экспоненциальный множитель, r²= x² + y² + z². Числа l и m определяют угловую часть ОГТ в декартовых координатах: их сумма (l+м+n) аналогична угловому квантовому числу для атомов и используется, чтобы обозначать функции s-типа (l=0), p-типа (l=1), d-типа (l=2), f-типа (l=3), и т.д. Строго говоря, декартовы ОГT не являются орбиталями: они лишь простые и удобные математические функции, которые часто называют гауссовыми примитивами.

Ортогональные волновые функции – две функции ψ₁ и ψ₂ являются ортогональными, если интеграл S₁₂= ∫dv ψ^*₁(r) ψ₂(r) равен нулю. S₁₂ называется интегралом перекрывания. Ортогональными являются собственные функции эрмитового оператора, соответствующие различным собственным значениям.

Особые точки скалярной функции – точки, в которых значения первых производных функции по аргументам равны нулю. Различают следующие типы особых точек: минимум, максимум, локальный минимум (а), седловая точка (б), максимум (в).

Особые точки поверхности потенциальной энергии – точки на поверхности потенциальной энергии (ППЭ), в которых выполняется условие стационарности: производная от потенциальной энергии U по всем нормальным колебательным координатам Q_i (координат Q_i, в базисе которых матрица Гессе диагональна) равна нулю: ¶U/¶Q_i = 0, i = 1, 2,…, 3N–6(5). В минимуме, отвечающем равновесному состоянию системы, все собственные значения матрицы вторых производных потенциальной энергии по координатам (матрицы Гессе Н_ij=¶² U/¶Q_i¶Q_j) положительны: Н_ii = ¶²U/¶Q_i² > 0. В седловой точке, отвечающей переходному состоянию - одномерном локальном максимуме - из нормальных координат одно и только одно из собственных чисел гессиана отрицательно. При квантово-химическом описании химических реакций предполагают, что реагентам, продуктам, пред- и послереакционным комплексам соответствуют локальные минимумы, а переходному состоянию – седловая точка ППЭ химической реакции.

Параметризация силового поля – подбор параметров для расчета потенциальных функций, определяющие так называемое силовое поле молекулы. Численное значение параметров выбирается так, чтобы получить согласие рассчитанных и экспериментальных характеристик молекулы. Параметрами являются равновесные межъядерные расстояния (длины связей) и валентные углы, а также силовые постоянные, то есть коэффициенты жесткости упругих сил, связывающих пары атомов. Простейшие модели молекулярной механики учитывают растяжения связей (Uраст.), деформацию валентных (Uдеф.) и двугранных (торсионных) углов (Uторс.), взаимодействие валентно несвязанных атомов, называемое также ван-дер-ваальсовым взаимодействием (Uвдв.), электростатические вклады (Uэл-стат.) и т.д.:

U = SUраст + SUдеф + SUторс + SUвдв + SUэл-стат.

Для каждого слагаемого записывается определенное аналитическое выражение (например, энергия электростатического вклада Uэл-стат описывается кулоновской функцией, возможно, с нецелыми зарядами на атомах в качестве параметров). Для описания потенциальной функции предельных углеводородов при умеренных требованиях к точности расчета достаточно около десяти параметров.

Дата добавления: 2015-06-04