I. Доказать общезначимость 3 страница

Правило 18 электронов - в устойчивых комплексах переходных металлов МL_n общее число валентных электронов на связях M-L и несвязывающих молекулярных орбиталях центрального атома равно 18.

p-электронное приближение - при решении уравнений Рутана для ненасыщенных и ароматических молекул, чаще всего являющихся плоскими, s-АО считают неполяризованными и включают в атомный остов, а движение p-электронов рассматривают в потенциальном поле таких остовов. Волновая функция молекулы при этом представляется как произведение y = y_s y_p, где y_s и y_p - нормированные антисимметричные по отношению к s- и p-электронам функции, соответственно. Их можно разложить по слейтеровским детерминантам, составленных только из s- и только из p-МО. Волновая функция y_s одинакова как для основного, так и для возбужденных состояний и все изменения связываются с p-электронами. Рассмотрение только p-электронов удовлетворяет вариационному принципу.

Поверхность потенциальной энергии – представление потенциальной энергии молекулярной системы как многомерной функции всех переменных (степеней свободы) в системе (например, длин связей и углов между ними). Потенциальная поверхность для молекулы с N атомами имеет 3N-6 независимых степеней свободы (три степени отвечают вращению и три - движению молекулярной системы). Важными особенностями потенциальной поверхности являются минимумы и седловые точки, которые представляют структуры переходных состояний, которые находят, оптимизируя геометрию молекул.

Полуэмпирические методы расчета – группа расчетных методов квантовой химии, использующих отказ от вычисления одноэлектронных и двуэлектронных интегралов, фигурирующих в методе ХФ. Вместо точного оператора Фока используется приближенный, элементы которого получают из эмпирических данных. Соответствующие параметры подбирают для каждого атома (иногда - с учетом конкретного окружения) и для пар атомов: таким образом, они являются либо фиксированными числами, либо зависят от расстояния между атомами.

Полуэмпирические методы намного быстрее, чем неэмпирические. Они применимы к большим (часто к очень большим, например - биологическим) системам и для некоторых классов соединений дают очень точные результаты. Однако это достигается за счет специально подобранных параметров, справедливых лишь в пределах узкого класса соединений. При переносе на другие классы, те же методы могут дать абсолютно неверные результаты. Кроме того, параметры расчета часто подбираются таким образом, чтобы воспроизводить те или иные молекулярные свойства, поэтому придавать физический смысл отдельным параметрам не следует.

Пренебрежение дифференциальным перекрыванием (NDO) – упрощение, применяемое в полуэмпирических квантово-механических расчетах. Считают, что из-за экспоненциального убывания АО двухэлектронными кулоновскими и обменными интегралами, содержащими произведения различ­ных атомных орбиталей, зависящих от одного аргумента, можно пренебречь. Уменьшает число интегралов, описывающих в расчете взаимодействия электронов.

Полное пренебрежение дифференциальным перекрыванием (ППДП, англ. CNDO) - один из первых полуэмпирических методов. Используется для вычисления электронных свойств основного состояния систем с закрытой оболочкой, оптимизации геометрии и общей энергии. В настоящее время заменен более сложными полуэмпирическими квантово-химическими методами, такими как MNDO, AM1 и PM3.

Принцип сохранения орбитальной симметрии Вудворда-Хоффмана – носит общий характер и позволяет в ряде случаев предсказывать, будут ли соединения реагировать, по какому пути пойдет реакция и каких продуктов следует ожидать. Рассматриваются структура активных МО реагирующих веществ и знаки атомных орбиталей (АО), составляющих МО. Реакция называется разрешенной по симметрии, если в ходе ее симметрия активных МО (все участвующие в реакции занятые и вакантные МО реагентов и продуктов) сохраняется. Деление реакций на разрешенные и запрещенные по симметрии осуществляется с помощью корреляционных диаграмм. Корреляционную диаграмму взаимодействия между реагентами и продуктом строят простым соединением МО с одинаковой симметрией (S ® S и A ® A), учитывая, что разность энергий МО должна быть минимальна. Если это возможно и ни одна из соединяющих линий не пересекает нулевого уровня (правило непересечения), то реакция «разрешена» по симметрии.

Поляризационные функции – базисные функции, описывающие поляризацию орбиталей атомов соседями по молекуле. Состоят из функций с более высокими значениями орбитального квантового числа l, чем те, которые отвечают минимальному базису. p- и d-функции выступают как поляризационные функции для базисных функций для атомов с s электронами, d- и f- функции действуют как поляризационные функции для атомов с s и p электронами и д.т.

Порядок связи – мера простого, двойного или тройного характера связи. В теории молекулярных орбиталей в основу определения положен учет компенсации эффектов занятых электронами связывающих и разрыхляющих орбиталей (см. кратность связи по Герцбергу).

Постулат Хэммонда -связывает геометрию переходного состояния с тепловым эффектом реакции. По Хэммонду экзотермическим реакциям соответствует реагентоподобное переходное состояние, эндотермическим – продуктоподобное, теплонейтральным – лежащее примерно по середине между реагентами и продуктами.

Потенциал Букингема -основан на предположении об экспоненциальной зависимости сил отталкивания между молекулами от расстояния между ними. Используетсядля описания ван-дер-ваальсовых взаимодействий. Энергия взаимодействия между молекулами в этом случае зависит от расстояния R между ними: U(R) = be^-aR – cR^-6 – dR^-8; a, b, c, d – постоянные. Это выражение справедливо только для неполярных сферически-симметричных молекул. Для расчета энергии взаимодействия более сложных систем в эмпирический потенциал вводят поправки. Чаще всего расчеты проводят с использованием упрощенного потенциала Букингема, в котором пренебрегают членом, включающим R^-8, и рассматривают полное взаимодействие как сумму взаимодействий между всеми атомами подсистем.

Потенциал Леннарда-Джонса – служит для расчета энергии межмолекулярного взаимодействия. Основан на предположении о быстром возрастании сил отталкивания между молекулами на малых расстояниях, происходящем по закону R^-n. Потенциал Леннарда-Джонса (6-12) получают при n = 12, зависимость R^-6 в этом случае отражает наличие дисперсионных сил. Потенциальная энергия взаимодействия между системами не имеющими постоянных диполей описывается выражением U(r) = 4ε [(σ/r)¹² - (σ/r)⁶], где ε и σ – эмпирические константы, r – расстояние между взаимодействующими системами; (σ/r)¹²- описывает отталкивание, (σ/r) ⁶ – описывает притяжение между системами.

Потенциал ионизации - энергия, которую необходимо сообщить системе, чтобы удалить какой-либо из ее электронов. По потенциалу ионизации можно судить о прочности связи электрона данной орбитали с атомным остовом.

Предел сходимости - вычисление методом ССП заканчивается, когда различие в энергии после двух последовательных итераций становится меньше, чем некая малая величина величина. Для полуэмпирических вычислений практический предел сходимости равен примерно 10^-3 (по умолчанию 0,01 ккал/моль), для неэмпирических - 10^-4-10 ^-5.

Приближение Борна-Оппенгеймера состоит в отделении движения ядер от электронного движения. Ядра намного тяжелее электронов и их можно считать неподвижными, рас-сматривая движение электронов относительно них. Уравнение Шредингера тогда может быть решено только для электронов при определенной ядерной конфигурации. Оправдано при квантово-химическом анализе поведения молекул в основном состоянии.

Приближение независимых частиц – наличие электрон-электронного отталкивания в гамильтониане не позволяет разделить координаты электронов и решить уравнение Шредингера аналитически для системы более двух электронов. Поэтому поведение каждого электрона описывается некоторой волновой функцией, подобно единственному электрону в атоме водорода, и зависит от поведения остальных электронов в среднем. В этом состоит суть приближения независимых частиц. Решения одноэлектронных уравнений – уравнений Хартри-Фока или Кона-Шэма – называются одноэлектронными волновыми функциями или орбиталями (в атоме - атомными орбиталями, в молекуле - молекулярными, в кристалле - кристаллическими). Для их расчета используется приближение самосогласованного поля.

Приближение самосогласованного поля (ССП) -в приближении независимых частиц действие всех остальных электронов на данный электрон заменяют средним полем, приближенно воспроизводящим их суммарное действие. Приближенная волновая функция (орбиталь) зависит от координат только рассматриваемого электрона: это дает возможность разделить переменные в уравнении Шредингера в сферической системе координат. Чтобы решить систему одноэлектронных уравнений с гамильтонианом, включающим усредненное межэлектронное взаимодействие, задают некоторый набор одноэлектронных функций, максимально близких к правильным, и с их помощью строят оператор, учитывающий отталкивание электронов. Затем решают набор одноэлектронных уравнений, возникающий из условия минимума среднего значения гамильтониана, вычисляемого с одноэлектронной волновой функцией. Полученные решения используют, чтобы построить "исправленный" оператор, вновь решают ту же систему уравнений, но теперь – с новым гамильтонианом и т.д. Процесс продолжается, пока получаемые собственные значения одноэлектронных энергий будут отличаться от полученных на предыдущей итерации лишь на очень незначительную величину. Этот процесс называется самосогласованием, а результирующее поле, создающее усредненный потенциал, называется самосогласованным полем.

Приближение центрального поля. Потенциал межэлектронного взаимодействия только в частных случаях (положительные одноэлектронные ионы, атомы инертных газов, атомы N, P и т.д.) сферически симметричен. Однако учет асферичности не улучшает заметно результат расчета, поэтому обычно используют усредненный по всем направлениям атомный потенциал, интегрируя его по углам. Вводимое таким образом приближение центрального поля позволяет рассматривать ССП-решения для любого атома как модифицированные решения для одноэлектронного водородоподобного атома. В этом случае потенциальная энергия зависит только от расстояния до ядра, т.е. сила притяжения к ядру носит центральный характер. Тогда переменные в уравнении Шредингера в сферических координатах разделяются и волновые функции, описывающие состояния электронов атома в пространстве (атомные орбитали), можно получить в аналитическом виде.

Растяжение связи - в эмпирической теории силового поля описывает изменение молекулярной потенциальной энергии при отклонение длины связи от равновесной. В классической теории силового поля термин растяжение связи представлен гармонической функцией.

Рентгеноструктурный анализ -рентгендифракционное исследование дает трехмерную атомную структуру веществ в кристаллическом состоянии. Эта структура отвечает минимальной энергией конформационных состояний или близкой к минимуму энергии. Атомные координаты, основанные на данных рентгеновской дифракции, часто используются для подготовки входных данных для квантово-химических расчетов. Они также могут служить как первичные данные для конформационного анализа. Анализ молекулярной упаковки дает также информацию о межмолекулярных контактах и межмолекулярных водородных связях.
РМХ (англ. - EHT) - расширенный метод Хюккеля - о дин из простейших полуэмпирических методов. Сформулирован Р. Хоффманном в начале шестидесятых годов. Не является методом самосогласованного поля. Расширенным методом Хюккеля получаюткачественное или полуколичественное описание молекулярных орбиталей и электронных свойств (например, заряды на атомах и распределение спиновой плотности). Удовлетворительно описывает распределение электростатического молекулярного потенциала (МЭСП). Не пригоден для оптимизации геометрии или молекулярно-динамических вычислений.

PM3 (параметрическая модель 3) - версия параметризации метода AM1; дает лучшие оценки теплот образования.

Свободная валентность – разность между максимально возможным полным порядком связи атома и его полным порядком связи в конкретном соединении. Отражает неполноту насыщения валентных возможностей данного атома.

Сгруппированные орбитали (СОГТ) – базисные функции, которые является линейной комбинацией гауссовых примитивов.

Секулярное уравнение – уравнение, возникающее при вариационном решении уравнения Шредингера путем минимизации выражения для энергии по варьируемым параметрам (коэффициентам разложения многоэлектронной волновой функции по частным волновым функциям φ_i):

| H_ij - ES_ij| = 0.

Здесь H_ij – матричный элемент оператора Гамильтона в базисе некоторых функций φ_i, Е – энергия состояния системы, S_ij – элемент матрицы интегралов перекрывания функций φ_i.

Силовое поле - используется в молекулярной механике, представляет собой функцию потенциальной энергии молекулы от координат ядер атомов (силы, действующие на атомы, представляются в виде функций координат атомов). Определяется через потенциальные функции (представляющими собой, например, суммы парных потенциалов взаимодействия атомов), которые содержат некоторые параметры, численное значение которых выбирается оптимальным образом так, чтобы получить согласие рассчитанных и экспериментальных характеристик молекулы. В простейшем случае параметрами являются равновесные межъядерные расстояния (длины связей) и валентные углы, а также силовые постоянные, то есть коэффициенты жесткости упругих сил, связывающих пары атомов. При использовании в молекулярной механике основываются на допущении возможности переноса этих параметров из одной молекулы в другую, так что численные значения параметров, подобранные для некоторых простых молекул, используются далее при прогнозировании свойств других более сложных соединений.

Силовая постоянная - коэффициент пропорциональности между возвращающей силой и смещением x простого гармонического осциллятора; сила = - k x. Большие силовые постоянные отвечают жестко связанным системам (возвращающие силы велики даже при малых отклонениях от положения равновесия). Частота колебаний определяется не только силовой постоянной, но и массой системы, так как чем больше масса, тем меньше эффективна возвращающая сила. Силовая постоянная является мерой жесткости связей между атомами и определяет (наряду с массой атомов) колебательные частоты молекул.

Собственная функция – функция называется собственной функцией оператора, если в результате его действия на данную функцию получается та же функция, умноженная на число.

Спин-орбиталь – одноэлектронная функция c_i (x_i), в аргумент которой вводят спиновую переменную s (x _i = r _i | s_i). Пренебрегая малым по величине спин-орбитальным взаимодействием, каждую спин-орбиталь c_i(x) можно представить в виде произведения пространственной орбитали c_i(r) и спиновой функции h(s): c_i(x) = c_i(r)h(s).

Спин-орбитальное взаимодействие – взаимодействие между спиновым и орбитальным магнитным моментами электрона. Сила взаимодействия зависти от их взаимной ориентации, а энергия этого взаимодействия проявляется в спектрах как тонкая структура.

Спиновые корреляции – относительное расположение электронов коррелировано со взаимным направлением их спинов. Дополнительно к кулоновскому отталкиванию, электроны с параллельными спинами проявляют тенденцию избегать друг друга. В этом проявляется внутреннее свойство электронов, которое следует из принципа Паули. Такое поведение влияет на среднее отталкивание двух электронов и на обменную энергию. Вероятность того, что электроны с параллельными спинами находятся в одной и той же точке пространства, равна нулю. Область пространства, в которой находится электрон с определенным направлением спина и в которую электроны с таким же направлением спина стремятся не попадать, называется дыркой Ферми.

STO-n G - сокращение, используемое в расчетах аb initio. Указывает используемый базисный набор, в котором орбитали слейтеровского типа, аппроксимированы n гауссианами. STO-n G (где n = 3, 4) - минимальный базисный набор; используется редко.

Спиновая плотность – разность между плотностями электронов с противоположными спинами. Для систем с закрытой оболочкой спиновая плотность равна нулю в каждой точке. Спиновая плотность на ядре определяет спектр электронного парамагнитного резонанса.

Структурная область – область, соответствующая минимуму на поверхности потенциальной энергии, внутри которой сохраняется стабильная конфигурация ядер, соответствующие ей распределение электронной плотности и система химических связей.

Суммарный заряд системы – суммарный избыток заряда ядра над электронным зарядом (или наоборот).

Суперпозиционная ошибка базисных наборов (англ. BSSE - basis set superpositional error) - вычисляя энергию взаимодействия молекул вариационным методом, следует скорректировать ошибку, возникающую из-за использования более широкого набора базисных функций, относящихся ко всем молекулам комплекса, по сравнению с базисом, в котором рассчитывалась каждая молекула в отдельности. Игнорирование этого факта ведет к искусственному занижению энергии комплекса, т.е. к завышенной энергии взаимодействия. Чтобы исправить эту ошибку, энергию каждой отдельной молекулы рассчитывают, включая в базис функции, центрированные на атомных центрах соседних молекул. При этом полагают, что заряды ядер последних равны нулю и берут число электронов, равным таковому в отдельной рассматриваемой молекуле.

Супрамолекулярная химия – область химии, изучающая химическое, физическое и биологическое поведение молекулярных ансамблей, обусловленное невалентными межмолекулярными взаимодействиями.

Сферические гармоники – набор функций угловых координат θ и φ, удовлетворяющих дифференциальному уравнению Λ ² Υ _lm (θ, φ) = - l(l+1) Υ _lm (θ, φ), где Λ² – оператор Лежандра. Их можно выразить в виде полиномов от sinθ, cosθ, sinφ, cosφ или в виде полиномов от переменных x, y, z. Угловые зависимости сферических гармоник и граничные поверхности атомных орбиталей не вполне идентичны. Последние определяются как границы областей пространства, заключающих в себе определенные значения амплитуды или плотности, и зависимость этих характеристик от радиуса (а не только от углов) искажает форму сферических гармоник.

Т

Теорема Бриллюэна - матричные элементы электронного гамильто­ниана между основной Y₀ и однократно-возбужденной Y₁ конфигурациями равны нулю. Позво­ляет понизить число вычисляемых матричных элементов гамильтониана ме­жду конфигурациями Y₀ и Y_k. Это означает, что однократно возбужденные состояния молекул с заполненной оболочкой непосредственно не смешиваются с основным состоянием, что свидетельствует о стабильности основного состояния, вычисленного методом самосогласованного поля.

Теорема вириала – устанавливает соотношение между полной энергией многоэлектронной системы (Е) и ее кинетической (G) и потенциальной компонентами (V): -V = 2G и Е = - G. Справедлива как для полной системы, находящейся в равновесии, так и для частей, из которых она образуется (для молекул и атомов).

Теорема Гельмана-Фейнмана – для точной и хартри-фоковской волновой функции справедливо соотношение 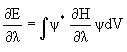, где l - некоторый параметр, от которого зависит энергия. Применение соотношения этого соотношения к изучению сил, действующих в молекуле известно под названием электростатической теоремы:

=Z_a ρ_{( ) dV +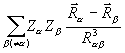} ( для ядра a молекулы), где ρ₍₎ – электронная плотность. Производная 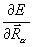описывает силу, действующую на ядро в молекуле. Ее компонента по одной из осей координат равна

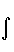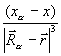F_xα = – Z_α ρ_{( )} dV + .

Сила, действующая на ядро а, есть сумма электростатического взаимодействия ядра а с электронной плотностью r и с другими ядрами. Пространство молекулы можно разделить на связывающую область, в которой электронная плотность создает электростатические силы, действующие на ядра по направлению друг к другу, и на антисвязывающую область, в которой силы, действующие на ядра, стремятся их раздвинуть. Такое разделение используется при анализе химической связи.

Теорема Купманса - если удалить с орбитали c_i один электрон (ионизировать атом или молекулу), то, считая, что после удаления электрона распределение остальных электронов останется “замороженным”, изменение энергии системы можно приближенно записать как 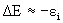. Хартри-фоковские орбитальные энергии e_i дают оценку потенциалов ионизации. Использование теоремы Купманса оправдано для молекул с жесткой структурой (для сопряженных углеводородов и др.), не изменяющих свою геометрию при ионизации.

Теория групп – математическая теория симметрии. В квантовой химии применяется для подбора подходящей линейной комбинации атомных орбиталей при построении молекулярных орбиталей молекулы, для классификации атомных и молекулярных состояний, определения правил отбора для переходов между этими состояниями и нахождения нормальных колебаний молекул.

Теория кристаллического поля – объясняет электронное строение комплекса в терминах возмущения АО центрального атома электростатическим полем лигандов, считающихся отрицательными точечными зарядами. Это возмущение полагается малым и приводит лишь к расщеплению энергетических уровней d- или f-элемента. Электронная конфигурация центрального атома рассматривается явно, тогда как лиганды – феноменологически. Распределение валентных электронов по расщепленным энергетическим уровням центрального атома определяется его сортом, величиной отталкивания электронов центрального атома от лигандов и взаимодействием электронов между собой.

Теория возмущений Мёллера-Плессета -теория возмущений, применяемая для учета многоэлектронных эффектов. Эффекты, вносимые корреляцией в движении электронов в каждый момент времени, учитываются как поправки к невозмущенным волновым функциям и уровням энергии, получаемым при расчетах по методу Хартри-Фока (в которых эффект электронной корреляции не учитывается в силу введенных приближений – приближения независимых частиц и самосогласованного поля). Разница между точным гамильтонианом H (где корреляция электронов учтена) и гамильтонианом нулевого порядка H₀ , в качестве которого выбирают оператор Фока F, рассматривается как возмущение: Н' = H – F. Уже учет поправок второго порядка теории возмущений позволяет учесть большую часть энергии электронной корреляции и значительно улучшает вычисления по сравнению с методом Хартри-Фока. Теория возмущений Мёллера-Плессета пригодна для описания дисперсионных взаимодействий, водородных связей и переходных состояний.

Теория поля лигандов - наиболее общий подход к рассмотрению электронной структуры комплексов. Рассматривает комплекс как целое на основе метода молекулярных орбиталей. Ввиду высокой симметрии координационного узла МО молекулы или иона координационного соединения классифицируются по симметрийным свойствам и принципиальную схему их образования из орбиталей лигандов часто можно построить, не проводя конкретных расчетов. Теория поля лигандов дает количественную картину образования МО комплекса.

Теория функционала плотности (ТФП, англ. - DTF). Согласно этой теории, все электронные свойства системы, включая энергию, могут быть получены из электронной плотности без знания волновых функций. Кинетическая энергия электронов описывается явно в приближении независимых частиц, классическая часть потенциальной энергии описывается по закону Кулона. Обмен и электронная корреляция учитываются приближенно. Расчеты по ТФП требует меньше компьютерного времени, чем вычисления другими методами, позволяя рассчитывать характеристики молекулярных систем с большим количеством атомов.

Топологическая теория химической связи, молекулярной и кристаллической структуры – основана на анализе электронной плотности. Строение многоэлектронной системы при ядерной конфигурации R определяется набором и сортами критических точек электронной плотности r(r,R) - точек r _c, где градиент электронной плотности Ñr(r,R) равен нулю. Пары градиентных траекторий, которые заканчиваются в двух соседних ядрах, начинаются в критической точке, имеющей одну положительную и две отрицательных значений кривизны электронной плотности (критической точке связи), определяют линию связи. Все траектории, которые заканчиваются на некотором ядре, определяют область пространства химической системы, которая называется бассейном этого ядра. Совокупность ядра и электронная плотность в пределах его бассейна определяет атом в химической системе. Каждая пара смежных бассейнов разделяется межатомной поверхностью, поток вектора rÑ через которую равен нулю. Таким образом, любая межатомная поверхность образуется градиентными траекториями, которые заканчиваются в критической точке связи r _b, лежащей на этой же поверхности. Если электронная плотность в критической точке связи превышает среднее значение электронной плотности в соседних точках, то лапласиан электронной плотности Ѳr(r _b) < 0; это признак концентрации электронов, характерный для ковалентной связи. В случае Ѳr(r _b) > 0 наблюдается деконцентрация электронов. Лапласиан электронной плотности прямо связан с локальными вкладами в электронную энергию молекулы и кристалла плотностей кинетической g(r) и потенциальной v(r) энергий (ħ²/4m)Ѳρ(r) = 2G(r) +V(r). Поскольку g>0, a v<0, то в областях, где происходит концентрация электронов, плотность потенциальной энергии выше.

Анализ лапласиана электронной плотности Ѳρ(r) в критической точке связи позволяет разделить все атомные взаимодействия на два класса. Если для электронной плотности здесь характерно доминирование отрицательной кривизны, то это означает, что электроны концентрируются вокруг критической точки связи и взаимодействие атомов можно отнести к ковалентному типу. Потенциальная энергия электронов в области, окружающей точку r _b, по меньшей мере, в два раза будет превосходить кинетическую энергию. Если же в точке r _b доминирует положительная кривизна электронной плотности, то электроны оказываются смещенными к каждому из взаимодействующих атомов и сконцентрированной в атомных бассейнах. Такие атомные взаимодействия считаются взаимодействиями ионного типа. В области, окружающей критическую точку связи, доминирует кинетическая энергия, а области, где доминирует потенциальная энергия, оказываются пространственно-разделенными.

Туннельный эффект – квантово-механическое явление прохождения частиц через потенциальный барьер. Возможность туннельного прохождения барьера проистекает из требования непрерывности волновой функции на стенках ямы до и после барьера. Вероятность туннельного прохождения тем меньше, чем выше высота относительная барьера и больше масса частицы. Очень эффективно совершают туннельное прохождение электроны, хуже - протоны.

Узлы волновых функций – точки, линии или поверхности, в которых волновые функции обращаются в нуль. Таким образом, вероятность найти электрон в узле равна нулю. Число узлов атомной радиальной функции равно n-l-1, ее угловой составляющей равно l, общее число узлов равно n-1.

Дата добавления: 2015-06-04