Элементы теории графов

Структурный анализ систем

При проектировании и изучении систем приходится анализировать боль­шое количество связей элементов и явлений, подвергать их всесто­рон­нему ис­следованию. Одним из воз­мож­ных направлений исследова­ния сис­тем является структурный анализ систем, базирующийся на тео­рии от­но­шений и теории графов и сетей. Важной особенностью струк­тур­ного ана­лиза является то, что, используя минимум исходных данных, он дает, по крайней мере, качественно достоверные результаты и поз­во­ляет сравнивать между собой различные ва­рианты проектов на ран­них стадиях разработки. Это важно, так как на стадии экс­плуа­тации до­ро­же всего обходится ис­прав­ление ошибок, допущенных при проек­ти­ро­вании.

Структурный анализ позволяет:

1) представить удобное символическое изображение системы в виде струк­турной схемы;

2) определить значимость элементов системы и связей между ними;

3) оценить качество структуры системы и сформулировать рекоменда­ции по ее улучшению.

Важной частью исследования является определение значимости эле­мен­тов системы на основании наличия между ними определенной со­во­­куп­ности от­но­шений. Для этого вводится количественный показатель зна­чимости - ранг элемента, который является относительной характе­рис­тикой, так как зависит от выбора критерия ранжировки. Определе­ние ранга эле­мен­тов позволяет облечь качественное субъективное пони­ма­ние значимости в коли­чест­венную форму.

Ранги элементов и другие структурные параметры позволяют оце­нить вклад, вносимый в общий функциональный показатель системы от­дель­ными элементами и связями, степень функциональной загрузки элемен­тов и связей, наличие "узких" мест в связях между объек­тами. Это, в свою оче­редь, позво­ляет разработать рациональную программу тех­ни­чес­кой реа­ли­зации системы с учетом значимости ее элементов, что дает оп­ре­деленную эко­номию сил и средств, поскольку выявленные проб­ле­мы решаются до начала не только про­из­водственного процесса, но и де­таль­но­го исследо­ва­ния системы.

После этих предварительных замечаний перейдем к изложению эле­ментов дискретной математики, которые нам понадобятся для изло­же­ния конкретных методов структурного анализа систем.

Def. Множество 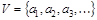и набор U пар элементов 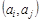из V называется графом G = (V,U).

Элементы множества V называются вершинами графа. Элементы на­бора U называются ребрами графа. Про ребро 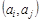говорят, что оно соединяет вершины . Ребра вида 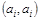называются петлями.

Вершины, соединенные ребром, назы­ваются смежными. Ребра, име­ю­щие общую вершину, называются смежными.

В наборе U могут встречаться одинаковые пары, ко­торые назы­вают­ся кратными (или параллельными) ребрами. Коли­чест­во одина­ко­вых пар 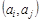в U назы­вается кратностью ребра .

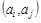В литературе граф с кратными ребрами и петлями обычно назы­вают псев­до­графом. Псевдограф без петель (но с кратными ребрами) называют мульти­графом. Собственно гра­фом, как правило, называют псевдограф без петель и кратных ребер. Такого определения мы и бу­дем придерживаться.

Если пары в наборе U являются упорядоченными, то граф назы­ва­ет­ся ориентирован­ным или кратко орграфом. Ребра орграфа часто на­зы­вают дугами. В дальней­шем мы огра­ничимся рассмотрением только орграфов, со­хра­нив при этом терминологию, используемую для графов. Так часто делают в специальной литературе, если это не вызывает пу­таницы.

Если 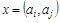- ребро графа, то вершина 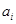называется нача­лом ребра x, а вершина - концом ребра x. В этом случае говорят, что ребро x соеди­няет вершины . Если вершина a является началом или концом ребра x, то говорят, что a и x инцидентны.

Два ребра называются смежными, если имеют общую вершину. Две вершины 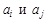называются смежными, если .

Степенью вершины a называется число ребер, инцидент­ных вершине a. Вершина графа, имеющая степень 0, называется изолиро­ван­ной, а степень 1 – висячей.

Если множество V и набор U состоят из конечного числа элементов и пар, то граф G называется конечным.

Граф, у которого любые две вершины соединены ребром, назы­вает­ся полным.

Система ребер называется пу­тем, соединяющим вершины , если конец каждого ребра (за ис­ключением последнего) совпадает с началом следующего. Для любого ребра, принадлежа­ще­го пути 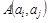, го­ворят, что путь 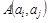про­хо­дит через это ребро. Аналогично, если вершина 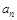принад­ле­жит неко­то­рому ребру пути 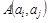, то говорят, что этот путь проходит через вер­шину .

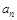Путь , не проходящий дважды ни через одно ребро, назы­вает­ся циклом.

Граф G называется связным, если для его любых двух различных вер­шин 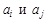существует путь, соединяющий эти вершины.

Весьма наглядной является геометрическая реализация графа G в виде фигуры Г, вершины которой соответствуют вершинам графа G, а ребрам графа G - отрезки прямых или дуги, соединяющие со­от­ветст­вую­щие вершины.

Справедлива следующая теорема.

Теорема. Каждый конечный граф G можно реализовать в трех­мер­ном евклидовом пространстве.

Для характеристики графа G используются следующие числовые ха­ракте­ристики:

1) число вершин графа (элементов) n;

2) число ребер графа (связей) m;

3) число его связных частей (компонент) p;

4) цикломатическое число v(G) = m - n + p;

5) хроматическое число графа v(G).

Смысл первых трех характеристик ясен без комментариев.

Цикло­ма­тическое число v(G) равно максимальному числу неза­ви­си­мых циклов.

Подробнее поясним смысл хроматического числа. Если все вершины графа окрашены kцветами так, что никакие две смежные вершины не окрашены одним цветом, то граф называется хромати­чес­ким по­рядка k. Минимальное число k, при котором граф является хрома­ти­чес­ким порядка k, называется хроматическим числом графа G и обозначается v(G), т.е. v(G) = min k.

Взяв в качестве вершин графа элементы системы, а в качестве ре­бер связи между ними, получаем структурную схему системы в виде вер­шин­­ного графа. Взяв в качестве ребер графа элементы системы, а в ка­честве вершин свя­зи между ними, получаем структурную схему сис­темы в виде реберного графа. Выбор типа графа определяется це­ля­ми иссле­до­вания. Существует ме­тодика преобразования вершинного графа в ре­бер­ный и наоборот. В даль­ней­шем изложении мы ограни­чим­ся рас­смот­рением только вершинных графов.

Представляя структуру системы в виде графа, мы получаем на­гляд­ную мо­дель системы. Заметим, что реальные системы характери­зу­ют­ся разно­об­ра­зием эле­ментов и связей между ними. Переходя к графу, мы абстра­ги­руемся от при­ро­ды и физической сущности объектов и свя­зей между ними.

Граф - это топологическая модель, отображающая некоторую сово­куп­ность связей между элементами системы.

Связь - это некоторое отношение между двумя элементами, т.е., исполь­зуя графы, мы имеем дело с бинарными отношениями. Сущест­вует математи­чес­кая дисциплина - теория отношений, изучающая бинарные отношения и опе­ра­ции с ними. В математике доказано, что бинарные отношения на конечном множестве образуют булеву алгебру. Элементы булевой алгебры изложены в приложении 1.

Дата добавления: 2015-06-04