
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Комплексні числа. Алгебраїчна, геометрична, тригонометрична і показникова форми запису комплексного числа. Дії над комплексними числами
|
|
|
|
ОБРАЗЕЦ ОФОРМЛЕНИЯ ТИТУЛЬНОГО ЛИСТА КОНТРОЛЬНОЙ РАБОТЫ
Рекомендуемая литература
Основная литература
1. Коммерческое (предпринимательское) право: учебник в 2 т. Т. 1. – 4-е изд., перераб. и доп. / под ред. В. Ф. Попондопуло. – М.: Проспект, 2009. – 592 с.
2. Коммерческое (предпринимательское) право: учебник: в 2 т. Т. 2. – 4-е изд., перераб. и доп. / под ред. В. Ф. Попондопуло. – М.: Проспект, 2009. – 608 с.
3. Коммерческое (торговое) право: учебник / под ред. Ю. Е. Булатецкого. – М.: Норма: ИНФРА-М, 2011. – 736 с.
4. Пугинский Б. И. Коммерческое право России. Учебник. – 2-е изд. – М.: Издательство «Зерцало», 2007. – 350 с.
Дополнительная литература
1. Андреева Л.В. Коммерческое право России: учебник. – М.: Волтерс Клувер, 2006. – 288 с.
2. Круглова Н.Ю. Коммерческое право: учебник. – М.: Высшее образование, 2009. – 749 с.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КАЛИНИНГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра социальных наук,
педагогики и права
Контрольная работа по дисциплине КОММЕРЧЕСКОЕ ПРАВО
(название дисциплины)
Тема № _____________________________________________
(полное название темы)
Выполнил (а) студент (ка)_____________________________
(Ф.И.О. полностью)
Учебная группа____________ шифр____________________
(номер зачётной книжки)
Контрольная работа
сдана___________________________
(дата сдачи)
Контрольную работу Допущена к защите
проверил ЮРАСЮК Н.В. ___________________________
(Ф.И.О. преподавателя) (дата и подпись преподавателя)
Контрольная работа
зачтена__________________________
(дата и подпись преподавателя)
Калининград
[1] Введение и заключение в контрольной работе – на усмотрение студента
[2] Контрольную работу можно направить по электронному адресу преподавателя borisova-65@mail.ru
Комплексні числа складають клас математичних об’єктів, які визначаються описаними нижче властивостями.
Кожному комплексному числу 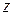 можна поставити у відповідність єдину упорядковану пару
можна поставити у відповідність єдину упорядковану пару  дійсних чисел
дійсних чисел 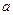 та
та 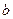 і навпаки. Сума і добуток двох комплексних чисел
і навпаки. Сума і добуток двох комплексних чисел 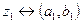 і
і 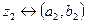 визначаються відповідно
визначаються відповідно 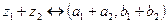 і
і 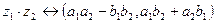 . Дійсні числа
. Дійсні числа 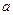 – комплексні числа
– комплексні числа 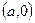 . Уявна одиниця
. Уявна одиниця 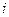 , визначається
, визначається 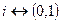 , тоді
, тоді 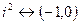 , тобто дійсне число
, тобто дійсне число 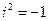 . Тому кожне комплексне число
. Тому кожне комплексне число 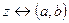 може бути записане у вигляді суми
може бути записане у вигляді суми 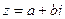 дійсного числа
дійсного числа 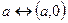 і чисто уявного числа
і чисто уявного числа 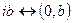 . Така форма запису називається алгебраїчною, при цьому
. Така форма запису називається алгебраїчною, при цьому 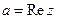 – дійсна частина
– дійсна частина 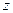 ,
, 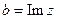 – уявна частина
– уявна частина 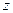 .
.
 Геометрично комплексне число можна інтерпретувати, як точку площини з декартовими координатами
Геометрично комплексне число можна інтерпретувати, як точку площини з декартовими координатами 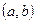 , або вектор площини з координатами
, або вектор площини з координатами 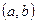 .
.
З цього легко випливає тригонометрична форма запису комплексного числа
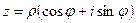 ,
,
де  ,
,
і називається модулем комплексного числа 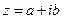 .
.
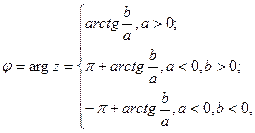
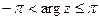 ;
; 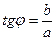
і називається головним значенням аргументу комплексного числа 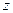 .
.
Так як кожній точці на комплексній площині можна поставити у відповідність безліч значень аргументу, які відрізняються на 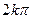 , то
, то
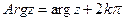 .
.
Крім того, використовуючи формулу Ейлера 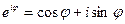 , отримуємо показникову форму запису комплексного числа
, отримуємо показникову форму запису комплексного числа 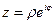 .
.
Використовуючи різні форми запису комплексних чисел, отримуємо результати дій над числами.
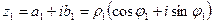 ;
; 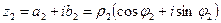
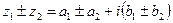
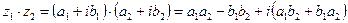
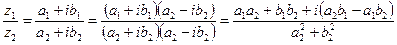
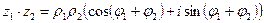
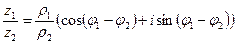
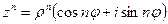
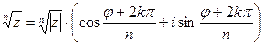 ,
,  .
.
Більш детальне викладення цього матеріалу див. [1, 2, 3].
Приклад 1
Обчислити 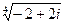 .
.
Розв’язання
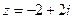 ,
, 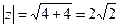 ,
,
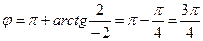 .
.
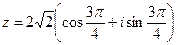
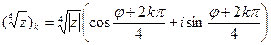 ,
, 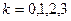 .
.
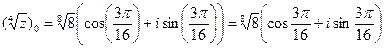 ,
, 
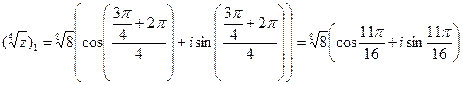 ,
, 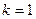
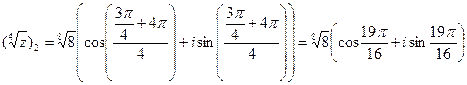 ,
, 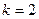

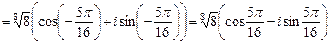 ,
, 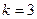 .
.
Вправи
1. Виконати дії:
1)  ; 2)
; 2) 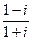 ; 3)
; 3) 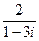 ; 4)
; 4) 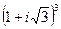 ; 5)
; 5) 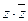 ; 6)
; 6) 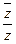 .
.
2. Знайти модуль і аргумент та представити в тригонометричній формі:
7) 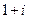 ; 8)
; 8) 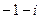 ; 9)
; 9) 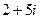 ; 10)
; 10) 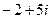 ; 11)
; 11) 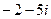 .
.
3. Обчисліть:
12) 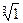 ; 13)
; 13) 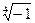 ; 14)
; 14) 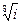 ; 15)
; 15) 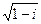 .
.
4. Визначте геометричний зміст:
16) 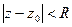 ; 17)
; 17) 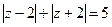 ; 18)
; 18) 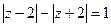 ;
;
19) 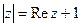 ; 20)
; 20) 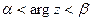 .
.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1306; Нарушение авторских прав?; Мы поможем в написании вашей работы!