Расчет элементов соединительных рамп

Пакет прикладных программ по проектированию развязок движения в разных уровнях, разработанный в Союздорпроекте (автор В.А. Федотов), охватывает практически все возможные случаи проектирования плана лево- и правоповоротных соединительных рамп развязок. Каждую соединительную рампу рассчитывают самостоятельно и она может быть представлена последовательностью сопрягающихся между собой геометрических элементов, образующих соединительную кривую, сопрягающуюся обеими концами с осями прямолинейных участков дорог на пересечении или с касательными к криволинейным участкам.

В пакете прикладных программ предусмотрены все представляющие практический интерес случаи сопряжения геометрических элементов между собой. Для замкнутого аналитического описания всей соединительной кривой каждый ее элемент представляют в локальной системе координат, а прямые и круговые кривые представляют также и в общей системе координат (рис. 33.7).

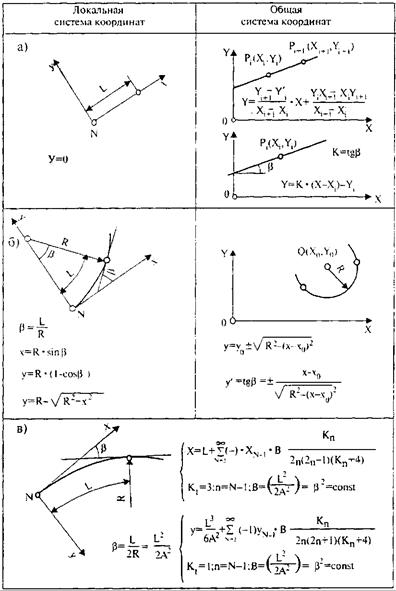
Рис. 33.7. Аналитическое выражение основных элементов соединительной кривой:
а - прямая; б - круговая кривая; в - клотоида

Различают простые и сложные соединительные кривые. К простым соединительным кривым относят кривые, представленные последовательностью следующих элементов: переходная кривая (ПК-1) - круговая кривая (КК) - переходная кривая (ПК-2). Эти элементы образуют выпуклое очертание, характерное для петлеобразных левоповоротных соединительных рамп (рис. 33.8, а), и вогнутое очертание, характерное для правоповоротных соединительных рамп (рис. 33.8, б). Простые соединительные кривые характеризуются наличием одного центра постоянной кривизны. К сложным соединительным кривым относят кривые, характеризуемые наличием двух и более центров постоянной кривизны.

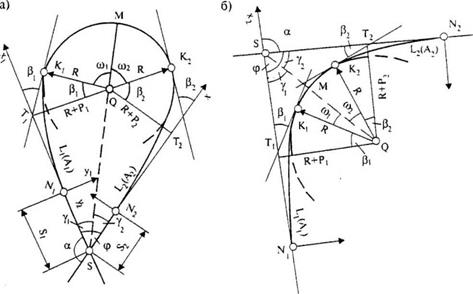
Рис. 33.8. Простая соединительная кривая:
а - выпуклая; 6 - вогнутая

Автоматический расчет простых соединительных рамп выпуклого или вогнутого очертания и аналитическое размещение их между осями пересекающихся прямолинейных участков дорог или касательными к осям криволинейных участков выполняют на основе следующих исходных параметров:

j - внутренний угол пересечения между криволинейными участками дорог или касательными к криволинейным участкам, в котором должна быть размещена соединительная кривая;

R - радиус круговой кривой;

D R - шаг изменения радиуса. Первоначально заданный радиус автоматически может быть изменен, если в процессе расчета будет установлена невозможность размещения соединительной кривой в заданный угол при назначенных исходных параметрах;

В ₁, В ₂ - ширины полос проезжих частей, с которых и к которым происходит ответвление и примыкание соединительных рамп;

i_{В 1}, i_{В 3} - поперечные уклоны проезжей части на соответствующих полосах;

В ₂ - ширина проезжей части соединительной рампы;

i_{В 2} - поперечный уклон проезжей части (виража) в пределах круговой кривой;

J - изменение центробежного ускорения;

i_д - увеличение поперечного уклона на переходной кривой при отгоне виража (по внешней кромке проезжей части);

L_1Т (А_1Т), L_2Т (А_2Т) - длины или параметры соответствующих переходных кривых, назначенные из определенных условий на основе первоначальной графической проработки. В случае отсутствия требований, устанавливающих длины или параметры переходных кривых, последние определяются автоматически по условию разделения кромок проезжих частей и возможности отгона виража;

S₁ и S₂ - расстояния от конечных точек N₁ и N₂ соединительной кривой до точки пересечения осей автомагистралей.

В результате автоматического расчета инженер-дорожник получает следующую информацию:

L₁ (А₁), L₂ (А₂) - оптимальные длины и параметры переходных кривых;

g ₁, g ₂ - углы положения центра круговой кривой Q относительно прямолинейных участков автомагистралей и точки их пересечения S;

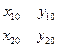- координаты центра кривой в локальных системах координат каждой переходной кривой;

SN₁, SN₂ - расстояния от точки пересечения автомагистралей до точек ответвления и примыкания соединительных кривых;

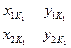- координаты точек начала К₁ и конца К₂ круговой кривой в локальной системе координат соответствующей переходной кривой;

S_Q - расстояние от точки пересечения осей автомагистралей до центра круговой кривой Q;

w₁, w₂ - углы, стягивающие части круговой кривой между направлениями SM со стороны каждой переходной кривой.

Одновременно определяют и все другие параметры, необходимые для построения рампы.

Сложные соединительные кривые, имеющие несколько центров постоянной кривизны, представляют последовательность сопряженных между собой (т.е. имеющих общую касательную в точке сопряжения) отрезков переходных кривых. При этом в качестве переходных кривых, входящих в состав сложных соединительных кривых, вследствие относительно небольших и практически постоянных скоростей движения обычно используют клотоиду, оптимальная длина которой:

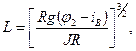где

R - радиус сопрягающей круговой кривой, м;

g - ускорение свободного падения, м/с²;

j ₂ - расчетный коэффициент поперечного сцепления колеса с дорогой;

i_B - уклон виража в пределах круговой части кривой;

J - изменение центробежного ускорения, м/с³.

Расчеты сложных соединительных кривых сводятся к решению с использованием компьютерной техники конечного числа частных задач сопряжения элементов, т.е. к решению уравнений, в которых в качестве переменных принимают параметр одной из клотоид А₁. Математические выражения основных параметров кривых, оформленные в виде отдельных операторов (процедур), представлены в табл. 33.1.

Таблица 33.1.

Математические выражения основных параметров кривых

Искомый параметр	Условное обозначение	Математическое выражение	Исходный параметр	Функциональная зависимость для оформления процедуры
Абсцисса любой точки	x		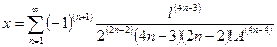l, A	x = f 1(l, A)
Абсцисса точки с заданным в ней радиусом кривизны		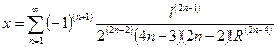l, R	x = f 2(l, R)
Ордината любой точки	y		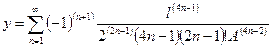l, A	y = f 3(l, A)
Ордината точки с заданным в ней радиусом кривизны		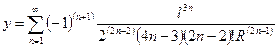l, R	y = f 4(l, R)
Абсцисса центра круговой кривой	x0		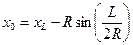l, R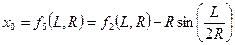
Ордината центра круговой кривой	y0		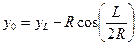l, R
Сдвижка	P	p = y0 - R	L, p	p = f 7(L, R) = f 6(L, R) - R
Параметр клотоиды	А	y0 = R - p = 0	R, p	A = f 8(R, p) = f 7(L, R) - p
Длина от начала до любой точки	L		x, А	L = f 9(x, А) = x - f 1(l, A)
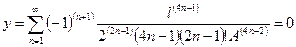
	y, А	L = f 10(y, А) = y - f 3(l, A)
Длина от начала до точки с заданным в ней радиусом кривизны	LR		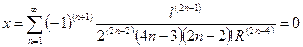x, R	LR = f 11(x, R) = x - f 2(l, R)
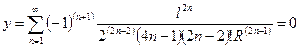
	y, R	LR = f 12(y, R) = y - f 4(l, R)

Компьютерная программа расчета сложных соединительных кривых включает решение следующих частных задач сопряжения геометрических элементов.

1. Сопряжение двух круговых кривых прямой линией. Комбинация элементов КК₁ - П - KK₂ (рис. 33.9). Для расчета задают координаты центров круговых кривых в общей системе координат Q ₁[ X_{Q 1}, Y_{Q 1}] и Q ₂[ X_{Q 2}, Y_{Q 2}], радиусы R ₁ и R ₂ с учетом правила знаков. В результате расчета определяют неизвестные коэффициенты уравнения общей касательной к заданным круговым кривым.

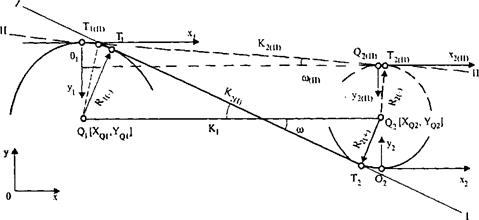
Рис. 33.9. Сопряжение двух круговых кривых прямой

2. Сопряжение круговой кривой с прямой посредством клотоиды. Комбинация элементов: КК - КЛ - П (рис. 33.10). В качестве исходных данных задают координаты центра круговой кривой в общей системе Q [ X_Q, Y_Q ], радиус R и уравнение прямой координатами двух точек или координатами одной точки и углом наклона к оси абсцисс общей системы координат. В результате расчета устанавливают длину или параметр сопрягающей клотоиды L (A).

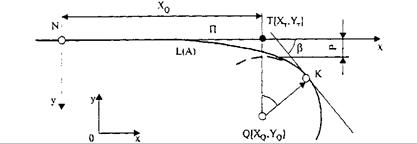
Рис. 33.10. Сопряжение круговой кривой с прямой посредством клотоиды

3. Сопряжение круговой кривой с двумя прямыми посредством клотоид. Комбинация элементов: П₁ - КЛ₁ - КК - КЛ₂ - П₂ (рис. 33.11). Задают уравнения прямых П₁ и П₂, каждое координатами двух точек в общей системе координат или соответствующими координатами одной точки и углом j между пересекающимися прямыми, а также другие исходные данные, используемые для расчета простых соединительных кривых. В результате расчета получают длины или параметры сопрягающихся клотоид L ₁(A ₁), L ₂(A ₂).

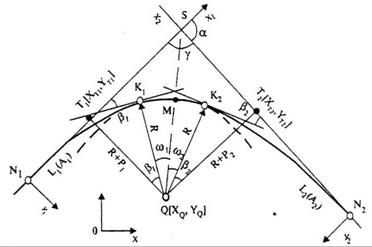
Рис. 33.11. Сопряжение круговой кривой с двумя прямыми посредством клотоид

4. Сопряжение двух круговых кривых клотоидами, переходящими в общую прямую. Комбинация элементов: КК₁ - КЛ₁ - П - КЛ₂ - КК₂ (рис. 33.12). В качестве исходной информации задают координаты центров круговых кривых Q ₁[ X_{Q 1}, Y_{Q 1}], Q ₂[ X_{Q 2}, Y_{Q 2}] и их радиусы со своими знаками R₁ и R₂, длины переходных кривых или их параметры L ₁(A ₁), L ₂(A ₂), или их отношение m = A ₁/ A ₂, а также сдвижки р ₁ и р ₂. В результате расчета устанавливают параметры уравнения сопрягающей прямой П.

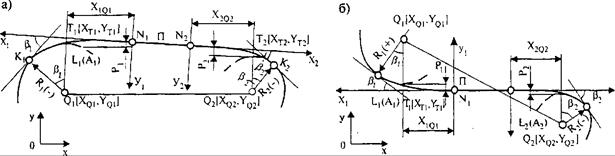
Рис. 33.12. Сопряжение круговых кривых с клотоидами:
а - односторонние кривые; б - обратные кривые

5. Сопряжение двух круговых кривых третьей круговой кривой. Комбинация элементов: КК₁ - КК₂ - КК₃ (рис. 33.13). Задают координаты центров круговых кривых Q ₁[ X_{Q 1}, Y_{Q 1}] и Q ₂[ X_{Q 2}, Y_{Q 2}] в общей системе координат, а также значения их радиусов R₁ и R₂. В результате расчета определяют координаты центра сопрягающей круговой кривой Q ₃[ X_{Q 3}, Y_{Q 3}], ее радиус R₃, а также координаты точек сопряжения B ₁[ X_{B 1}, Y_{B 1}] и B ₂[ X_{B 2}, Y_{B 2}].

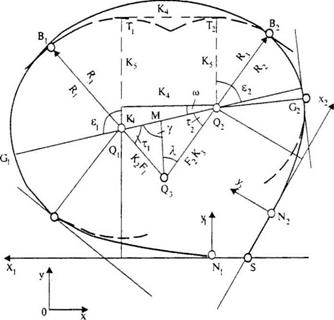
Рис. 33.13. Сопряжение двух круговых кривых третьей

6. Сопряжение двух круговых кривых двумя клотоидами.

Комбинация элементов: КК₁ - КЛ₁ - КЛ₂ - КК₂ (рис. 33.14). В качестве исходной информации задают координаты центров круговых кривых в общей системе координат Q ₁[ X_{Q 1}, Y_{Q 1}], Q ₂[ X_{Q 2}, Y_{Q 2}] и их радиусы со своими знаками R₁ и R₂, отношение параметров m = A ₁/ A ₂. В результате расчета устанавливают положение локальной системы координат, параметры клотоид L ₁(A ₁), L ₂(A ₂), а также координаты главных точек (N₁, N₂, К₁, К₂, Т₁, Т₂).

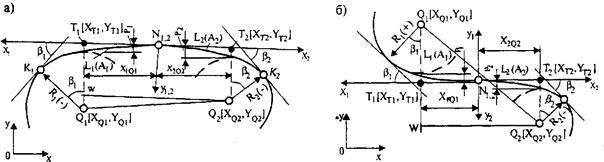
Рис. 33.14. Сопряжение двух круговых кривых соединяющимися клотоидами:
а - односторонние кривые; б - обратные кривые

7. Сопряжение двух круговых кривых двумя отрезками клотоид с круговой вставкой между ними. Комбинация элементов: КК₁ - КЛ₁ - КК₃ - КЛ₂ - КК₂ (рис. 33.15).

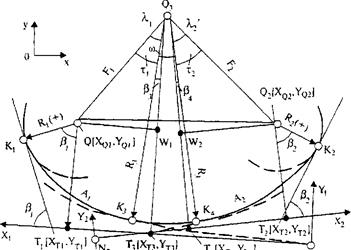
Рис. 33.15. Сопряжение двух круговых кривых внешними клотоидами с круговой вставкой между ними

В качестве исходной информации задают координаты центров круговых кривых Q ₁[ X_{Q 1}, Y_{Q 1}] и Q ₂[ X_{Q 2}, Y_{Q 2}], радиусы R₁ и R₂ со своими знаками, отношение параметров m и может быть также задан радиус сопрягающей кривой R₃. В результате расчета определяют параметры клотоид А₁ и А₂, радиус сопрягающейся с ними круговой кривой R₃, положение локальной системы координат и координаты главных точек (Q₃, K₁, К₂, К₃, К₄, N₁, N₂).

8. Сопряжение круговых кривых отрезком клотоиды. Комбинация элементов: КК₁ - КЛ - КК₂ (рис. 33.16).

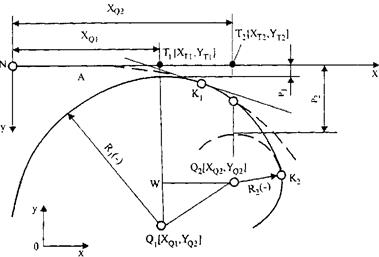
Рис. 33.16. Сопряжение двух круговых кривых отрезком клотоиды

Задают координаты центров круговых кривых Q ₁[ X_{Q 1}, Y_{Q 1}], Q ₂[ X_{Q 2}, Y_{Q 2}], радиусы R₁ и R₂. В результате расчета определяют параметр сопрягающей клотоиды А, положение локальной системы координат и координаты главных точек (К₁, К₂).

Использование метода сопряжения элементов позволяет весьма эффективно рассчитывать соединительные кривые право- и левоповоротных рамп практически любого очертания в плане. Однако при проектировании правоповоротных и директивно-направленных левоповоротных соединительных рамп, проектируемых в рамках существенно менее жестких ограничений по сравнению с левоповоротными петлеобразными рампами, возможен принципиально новый подход к решению плана соединительных рамп. Этот подход, во многом сходный с решением плана трассы основных дорог, реализован в Союздорпроекте в виде конкретного алгоритма и программы для компьютера.

В основе метода лежат принципы трассирования посредством кубических сплайнов. Суть метода, названного методом координатного задания оси трассы, состоит в следующем.

1. По плану в общей системе координат прорабатывают с использованием шаблонов или специальной гибкой линейки эскизный вариант сложной соединительной кривой.

2. Трассу задают координатами последовательности точек с шагом 40 - 60 м, снимаемых (лучше всего с помощью дигитайзера) с эскизной кривой.

3. Заданную последовательность точек аппроксимируют кубическими сплайнами (отрезками алгебраических полиномов, обычно третьей степени), обладающих высокой степенью гладкости, достигаемой посредством минимизации интеграла квадратов вторых производных по длине кривой:

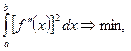
причем на отрезке а = х ₀ < х ₁,..., х_n = b каждому значению абсциссы соответствует значение ординаты y ₀, y ₁,..., y_n.

Задача сводится к нахождению аппроксимирующей функции S (x), называемой сплайном сетки А, интерпретирующей значения ординату, в узлах сетки. Основное соотношение для кубических сплайнов:

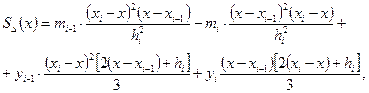где (33.5)

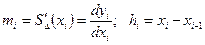
Требование непрерывности второй производной 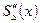в точках х_i, (i = 1, 2,..., п -1) выполняется при

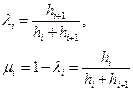
откуда следует:

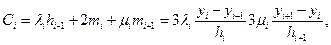где

i = 1, 2,..., п -1.

Система линейных уравнений имеет вид:

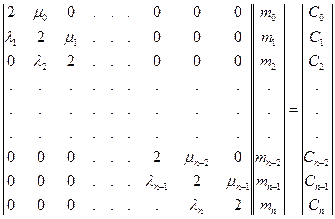(33.6)

Система линейных уравнений (33.6) (в левой части предопределена трехдиагональная матрица коэффициентов) решается методом прогонки, в результате чего определяются неизвестные коэффициенты в виде первых производных т ₁, т ₂,..., т_п, входящих в уравнение (33.5). Поскольку в начале и конце соединительной кривой направления определены касательными в точках ответвления и примыкания к осям пересекающихся автомагистралей, то при х = а и х = b соответственно задают.

Длина всей кривой определяется как сумма длин отдельных ее участков:

(33.7)

Кривизна соединительной кривой в любой точке со своим знаком:

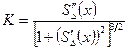(33.8)

4. Строят диаграмму кривизны сплайн-функции (рис. 33.7) и аппроксимируют ее в виде ломаной, представляемой отрезками прямых, параллельных и непараллельных оси абсцисс. Тогда соединительная кривая уже может быть предопределена известными элементами клотоидной трассы: прямыми, круговыми кривыми, клотоидами и отрезками клотоид. При этом на диаграмме кривизны этим элементам соответствуют: прямая, совпадающая с осью абсцисс; прямая, параллельная оси абсцисс, наклонная прямая, примыкающая одним концом к оси абсцисс; наклонная прямая.

Изложенный метод координатного задания оси соединительной кривой с последующей аппроксимацией кубическими сплайнами является весьма эффективным при проектировании правоповоротных и директивно-направленных левоповоротных соединительных рамп, особенно в случае криволинейного характера плана пересекающихся дорог и при наличии контурных ограничений.

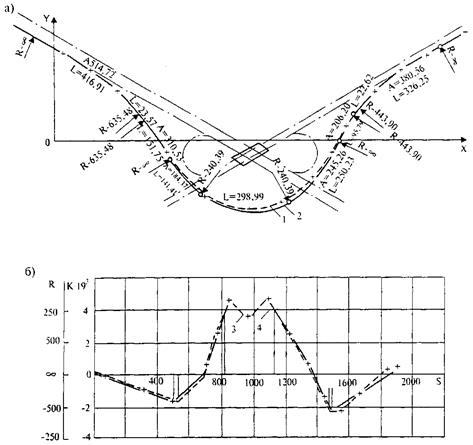
Рис. 33.17. Проектирование плана соединительных рамп по методу «кубических сплайнов»:
а - план соединительной рампы; б - диаграмма кривизны;
1 - эскизный план трассы; 2 - расчетный план трассы; 3 - диаграмма кривизны эскизной трассы; 4 - сглаженная диаграмма кривизны

Дата добавления: 2015-06-04