Учёт неопределённости и риска при оценке эффективности ремонта дорог

Очень часто при разработке проектов ремонта дорог возникают ситуации, при которых рассматриваемые ремонтные альтернативы могут иметь несколько, а в некоторых случаях и множество возможных исходов, характеризующихся различными значениями показателей их эффективности. Эти ситуации, как правило, обусловлены влиянием на процесс ремонта внешних по отношению к нему факторов, к основным из которых можно отнести экономическую конъюнктуру деятельности предприятия (спрос на услуги, цены на ресурсы, степень концентрации работ), природно-климатические условия, возможные отклонения в параметрах проектов (по производительности основных машин, стоимости и срокам выполнения и т.п.).

В таких ситуациях возникает необходимость принятия решений в условиях неопределенности или риска наступления возможных исходов осуществления проектов.

Под «неопределённостью» обычно понимают возможные состояния внешней среды, вероятности наступления которых неизвестны, что обусловлено, как правило, неполнотой и неточностью информации об условиях реализации проекта.

Под-«риском» в общем смысле этого слова понимают наступление таких состояний внешней среды, закономерности изменения которых известны или могут быть описаны с помощью известных законов теории вероятности.

В случае неопределённости исходов инвестиционного проектирования рекомендуется использовать критерий Гурвица [59].

По критерию Гурвица выбирается та альтернатива, которая ведет к получению наилучшего результата при промежуточных (устанавливаемых в зависимости от склонности к риску) оценках состояния внешней среды. Критерий Гурвица определяется из условия максимизации следующего выражения:

l _mах× ЧДД_ij + (1 – l) _min× ЧДД_ij, где

l - характеристика склонности к риску (l = 0..1);

ЧДД_ij - чистый дисконтируемый доход по i -тому варианту проекта и j -тому варианту состояния внешней среды.

Пример. Пусть для трех возможных состояний внешней среды j (j = 1,2,3) и трех альтернативных проектов ремонта i (i = 1,2,3) рассчитаны следующие показатели чистого дисконтируемого дохода (табл. 23.1). Требуется определить наилучший вариант ремонта по критерию Гурвица, если l = 0,5.

Таблица 23.1

Принятие решения в условиях неопределенности

Вариант проекта, i	ЧДДij при состоянии j:

Для нашего примера при l = 0,5 оптимальным является третий инвестиционный проект, так как критерий Гурвица (при i =1 - 0,5×(9 + 21) = 15; i =2 - 0,5×(1 + 18) = 9,5; i =3 - 0,5×(14 + 17) = 15,5) для него является максимальным.

При известных вероятностях возможных состояний внешней среды для принятия решений наиболее часто используют два критерия: критерий Байеса (максимум математического ожидания исхода) и максимум функции полезности.

Критерий Байеса определяется из следующего выражения:

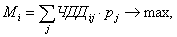где

р_j - вероятность j -того состояния внешней среды.

Этот критерий не учитывает расхождение результатов проекта (значений ЧДД) и поэтому является «нейтральным» по отношению к риску.

Критерий функции полезности наряду с математическим ожиданием возможных исходов учитывает и их среднее квадратическое отклонение s:

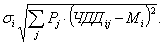(23.11)

При этом устанавливается функция полезности следующего вида:

U_i = M_i ± k × s_i ® mах, (23.12)

в которой выбор знака и коэффициента k при s зависит от склонности предприятия к риску (при положительном k - большая склонность к риску, при отрицательном k - меньшая).

Рассмотрим использование приведенных критериев на следующем примере (табл. 23.2).

Таблица 23.2

Принятие решения в условиях риска

Вариант проекта, i	ЧДДij при вероятности исхода рj
р 1= 0,2	р 2 = 0,3	р 3 = 0,5

Рассчитав математические ожидания возможных исходов по всем инвестиционным альтернативам:

М = 0,2×25 + 0,3×16 + 0,5×10 = 14,8;

М = 0,2×10 + 0,3×15 + 0,5×14 = 13,5;

М = 0,2×9 + 0,3×10 + 0,5×12 = 10,8;

получим, что по критерию Байеса следует выбрать первый проект.

Если же в качестве критерия использовать функцию полезности U_i = M_i - s_{i .max}, (предполагающую довольно низкую склонность к риску), то в этом случае, как видно из нижеприведенных расчетов, наиболее целесообразной является реализация второго варианта.

Действительно, так как:

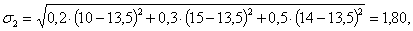
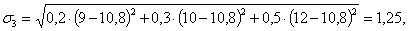
то U ₁ = 14,8 - 5,72 = 9,08; U ₂ = 13,5 - 1,8 = 11,7; U ₃ = 10,8 - 1,25 = 9,55, то есть значение U ₂ является максимальным.

В практике оценки эффективности инвестиционных проектов ремонта дорог рекомендуется использовать следующие методы учёта факторов их неопределённости и риска:

корректировки нормы дисконта;

построения дерева решений;

анализа чувствительности показателей эффективности;

имитационного моделирования.

Метод корректировки нормы дисконта предусматривает её увеличение до некой величины, гарантирующей высокую надёжность проекта (положительную величину интегрального эффекта). Корректировка осуществляется путём прибавления к норме дисконта так называемой «премии за риск», после чего производится расчет чистого дисконтируемого дохода и других показателей эффективности. В общем случае чем больше неопределенность и риск осуществления инвестиционного проекта, тем выше должна быть величина премии, которая может приниматься расчетным или экспертным путем, а также в соответствии с действующими инструкциями.

Метод построения дерева решений используется для анализа риска проектов в тех случаях, когда риски решений, принимаемых на различных этапах или в различные моменты времени их реализации, являются тесно взаимосвязанными между собой.

Алгоритм построения дерева решений применительно к анализу эффективности инвестиционных проектов предполагает следующую последовательность действий:

определение в виде стрелочной диаграммы эффектов и расходов при возможных структурных схемах реализации проекта;

установление вероятностей притоков и оттоков денежных средств для каждой альтернативной схемы по годам расчетного периода;

расчёт совокупной вероятности осуществления каждого сценария осуществления проекта и соответствующих этому сценарию результирующих показателей эффективности;

анализ полученных вероятностей распределений показателей эффективности и принятие решения об инвестировании.

Метод анализа чувствительности показателей эффективности предусматривает оценку степени влияния основных параметров проекта на его результирующие показатели: интегральный эффект, внутреннюю норму доходности и т.д. Проект считается надежным (устойчивым), если изменения его параметров в наиболее вероятных диапазонах их изменения не приводят к отрицательным значениям чистого дисконтируемого дохода.

Вычислительная процедура этого метода заключается в поочередном изменении в рамках возможных значений каждого из анализируемых параметров проекта при фиксированных (средних) значениях всех остальных параметров с последующей оценкой значимости каждого из них на величину результирующего показателя.

Метод имитационного моделирования предусматривает проведение серии расчетных экспериментов с целью проверки устойчивости проекта к изменению основных условий его реализации. Принципиальное отличие этого метода от предыдущего заключается в следующем.

Во-первых, предполагается, что рассматриваемые параметры инвестиционного проекта являются случайными величинами, распределение которых в заданном интервале подчиняется одному из известных законов распределения вероятностей.

Во-вторых, в процессе каждого эксперимента оценивается влияние на изучаемый показатель не отдельно взятого параметра (при неизменных значениях всех остальных), а всей совокупности анализируемых параметров, значения которых генерируются как случайные числа в принятых интервалах их изменения.

ГЛАВА 24. Планирование и анализ производственно-финансовой деятельности дорожных организаций по содержанию и ремонту автомобильных дорог

Дата добавления: 2015-06-04