Экспериментальная часть. Приборы и оборудование

Приборы и оборудование

Функциональная схема представлена на рисунке 7.7 где:

PQ – генератор звуковых сигналов;

PO – осциллограф;

ФПЭ-10 – модуль с колебательным контуром;

ФПЭ-08 – преобразователь импульсов;

ИП – источник питания$

МС – магазин сопротивлений.

Методика измерений.

В данной работе для исследования затухающих колебаний в реальном колебательном контуре, включающем активное сопротивление R, применяется электронный осциллограф. При этом через генератор звуковых колебаний производится периодическая подзарядка конденсатора, т.е. кривая затухающих колебаний периодически повторяется.

При не очень больших значениях сопротивления контура (, где L – индуктивность катушки, С – емкость конденсатора)), на экране осциллографа наблюдается картина затухающих колебаний, как это показано на рис.7.2, что соответствует закону изменения напряжения

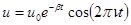
Если генератор задает частоту n, то цикл подзарядки конденсатора длится секунд, этому времени на экране осциллографа соответствует отрезок L₁. Периоду колебаний T соответствует отрезок L. Следовательно период затухающих колебаний может быть определен по формуле

.

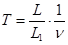Измерив амплитуды колебаний, отстоящие друг от друга на время, равное периоду

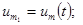
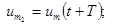
можно определить логарифмический декремент затухания

и его среднее значение

.

Тогда коэффициент затухания можно рассчитать как

.

Значение сопротивления в контуре можно изменять, например, с помощью магазина сопротивлений (R_м). Зависимость логарифмического коэффициента затухания от сопротивления R_м в контуре показана на рис.7.9. Полное активное сопротивление контура R складывается из активного сопротивления катушки индуктивности R_k и сопротивления магазина R_м:

.

Значение R_k можно определить, экстраполируя график до значения l ® 0. Тогда согласно формуле для коэффициента затухания , можно рассчитать индуктивность L катушки

и, считая b << w₀, емкость С конденсатора из формулы Томсона

.

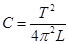При больших значениях сопротивления контура (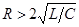) на экране электронного осциллографа будет наблюдаться апериодический процесс, показанный на рис.7.5.

Измерения логарифмического декремента затухания l можно проводить также с помощью фазовой кривой u=f(i). Если сопротивление контура , то фазовые кривые имеют вид, показанный на рис.7.4.

При больших значениях сопротивления контура (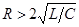) фазовая кривая для апериодического разряда принимает вид, показанный на рис.7.6.

Экспериментальная установка.

В работе для получения колебаний в контуре используется модуль ФПЭ-10 с контуром, изображенным на рис.7.8.

Происходящие в контуре затухающие колебания (рис. 7.2) наблюдаются на экране осциллографа. Цикл заряжения и разряжения осциллографа длится 1/n с, где n - частота, задаваемая звуковым генератором. На экране осциллографа ему соответствует отрезок L₁. Это позволяет определить период Т затухающих колебаний, которому на рис. 7.2 соответствует отрезок L. Из пропорции получаем:

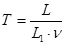(7.14)

Сигнал в форме гармонического колебания заданной частоты с генератора PQ преобразователем ПИ преобразуется в последовательность прямоугольных импульсов той же частоты. Будучи поданным на колебательный контур КК, импульс заряжает конденсатор С до напряжения U_m, сообщая контуру начальный запас энергии. По окончании импульса происходит многократный разряд конденсатора С через индуктивность L и сопротивление R, то есть возникают затухающие колебания (рис.7.2).

Изменение коэффициента затухания δ колебательного процесса осуществляется выбором величины резистора R магазина сопротивления МС.

Порядок выполнения работы:

Задание 1: Измерение периода, логарифмического декремента и параметров L, C, R колебательного контура.

1. Подать напряжение на схему, включить источник питания ИП, генератор PQ, осциллограф PO.

2. Установить следующие параметры выходного напряжения звукового генератора: частота 250 Гц, напряжение 3В.

3. На блоке преобразователя импульсов (ПИ) ФПЭ-08 нажать кнопки “ “ и правую клавишу “Скважность грубо”.

4. На магазине сопротивлений установить сопротивление R_M=100 Ом.

5. Воздействуя на ручки развертки и усилителя осциллографа, получить на его экране полную кривую затухающих колебаний и зарисовать ее.

6. Измерить расстояния L, L₁ и вычислить период колебаний по (7.14).

7. Измерить амплитуды колебаний U₀, U₁, U₂ и по формуле (7.9) вычислить логарифмический декремент затухания l. По формуле (7.10) определить коэффициент затухания b.

8. Результаты измерений занести в таблицу 7.1.

9. По формуле 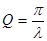рассчитать добротность Q. Результаты записать в таблицу10.1.

10. Выполнить измерения и расчеты по п.6-9 для сопротивлений: 100, 300, 500, 700, 900 Ом.

11. Построить график зависимости логарифмического декремента затухания l от сопротивления R_M (рис. 7.9), откладывая значения R_M по оси абсцисс от произвольной точки 0 и экстраполируя график к l=0. Полное сопротивление контура R складывается из сопротивления R_к катушки самоиндукции и сопротивления магазина R_м: R=R_к+R_м. Поэтому согласно (7.10)

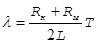(7.15)

Значение R_к определить графически из рис.7.9.

12. Используя полученные ранее значения R_к и периода Т, вычислить индуктивность L по формуле (7.15), а затем емкость C по формуле (7.11)

13. Опытным путем подобрать на магазине сопротивлений МС такое значение критического сопротивления R_МК, при котором в контуре будет наблюдаться апериодический процесс (рис. 7.6). Сравнить экспериментальное значение R_МК с величиной, полученной из выражения: .

Задание 2. Исследование фазовых кривых.

Для наблюдения на экране фазовой кривой на вертикально отклоняющие пластины осциллографа подают напряжение с обкладок конденсатора, а на горизонтально отклоняющие пластины – напряжение U_R с клемм магазина сопротивлений R_М, пропорциональное току 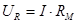. Таким образом, на экране осциллографа изображается зависимость напряжения U на обкладках конденсатора от тока I в контуре.

1. Установить на магазине сопротивлений МС сопротивление 100 Ом, на звуковом генераторе – частоту 250 Гц.

2. Включить осциллограф. Получить на экране фазовую кривую (рис. 10.4). Установить картину в центре экрана. Зарисовать фазовую кривую.

3. Непосредственно на фазовой кривой измерить значения напряжения и тока, отличающиеся по времени на период колебаний. Для этого определить расстояние от центра координат 0 фазовой плоскости до точек пересечения спирали с осями напряжения U и тока I. Вычислить логарифмические декременты затухания λ для напряжения и тока по (7.9’, 7.9’’). Измерения выполнить по всем виткам фазовой кривой. Результаты измерений занести в таблицу 7.2.

4. Повторить измерения по пунктам 3, 4 при значения сопротивления магазина R_м 200, 300, 400, 500, 600, 700 Ом.

5. Получить апериодический процесс в колебательном контуре и зарисовать для него фазовую кривую.

6. Рассчитать погрешность определения λ:

;

где ΔU – погрешность измерения U на экране.

Таблица 7.1

RM, Ом

ν, Гц

L, дел

L1, дел

Т, с

U0, дел

U1, дел

U2, дел

λ

b, с^-1

Q

L, Гн

C, Ф

Rк, Ом

Rмк, опыт

Rмк теор

Таблица 7.2

RM, Ом	R=Rк+Rм, Ом	U10, дел	U20, дел	U30, дел	λU	I10, дел	I20 дел	I30 дел	λI

Контрольные вопросы

1. Что такое колебательный контур?

2. Нарисуйте схему последовательного колебательного контура.

3. Объясните механизм возникновения электромагнитных колебаний в колебательном контуре.

4. Напишите дифференциальное уравнение затухающий колебаний и его решение.

5. Напишите формулы для коэффициента затухания, собственной частоты колебаний контура, декремента и логарифмического декремента затухания.

6. При каких условиях в колебательном контуре возникает апериодический процесс?

7. Сформулируйте понятия фазовой плоскости и фазовой кривой.

8. Нарисуйте фазовые кривые для затухающего колебательного и апериодического процессов в колебательном контуре.

Литература:

1. Савельев, И.В. Курс общей физики: В 3-х т./ И.В.Савельев.- М.: Наука. 1989. – Т.2. – 496с., гл. 13.

2. Калашников С.Г. Электричество. – М.: Наука, 1986.

3. Трофимова, Т.И. Курс физики: Учебное пособие для вузов/ Т.И. Трофимова. – М.: Высш. шк. 1999. – 542 с., § 146.

4. Детлаф, А.А. Курс физики: Учебное пособие для вузов/ А.А. Детлаф, Б.М. Яворский. – М.: Высш. шк., 2002.-718 с., § 28.1.

5. Лозовский, В.Н. Курс физики: Учебник для вузов: В 2 т. Т.1./ Под ред. В.Н. Лозовского. – СПб.: Издательство "Лань", 2000. – 576 с., §3.8.

Лабораторная работа 2-19

Дата добавления: 2015-06-04