Теоретическое введение. Порядок выполнения работы

Порядок выполнения работы

Задание 1: Измерение коэффициентов взаимной индукции М₂₁ и М₁₂ и исследование их зависимости от взаимного расположения катушек.

1. Подать напряжение на установку.

2. Ознакомиться с работой электронного осциллографа и звукового генератора.

3. Задать напряжение U_эфф=2 В и частоту сигнала генератора f=10 кГц, подать напряжение на катушку 1, а ЭДС катушки 2 подать на осциллограф (переключатели П₁ и П₂ в крайнее левое положение). Положение переключателя “V/дел” на передней панели осциллографа РО установить 0,05 В/дел.

4. Установить подвижную катушку 1 в крайнее переднее положение. Перемещая ее в противоположное крайнее положение через 1 см, записывать значение координаты Z (расстояние между центрами катушек) и ЭДС взаимной индукции в цепи катушки 2 ε₀₂ в табл. 3.1.

5. По формуле (3.10) рассчитать значение М₂₁. Полученные данные занести в таблицу 5.1.

6. Поменяв местами катушки L₁ и L₂ (переключатели П₁ и П₂ в крайнее правое положение), повторить измерения по п.п. 3, 4 и рассчитать М₁₂.

7. Построить графики зависимости М₂₁ и М₁₂ как функции координаты Z (расстояние между центрами катушек 1 и 2).

Задание 2: Измерение М₂₁ при различных значениях амплитуды питающего напряжения.

1. Поставить катушку 1 в среднее положение относительно катушки 2. (Выдвинуть шток до положения “50”).

2. Задать частоту звукового генератора PQ f=20 кГц).

3. Измерить амплитуду ЭДС взаимной индукции ε₀₂ при различных значениях напряжения U_эфф в цепи катушки 1 в интервале 0 – 5 В через 0,2 В.

4. По формуле (3.10) рассчитать М₂₁. Полученные данные занести в таблицу 3.2.

Задание 3: Измерение М₂₁ при различных частотах питающего напряжения.

1. Поставить катушку 1 в среднее положение относительно катушки 2. (Выдвинуть шток до положения “50”).

2. Задать напряжение звукового генератора U_эфф=2,5 В.

3. Измерить амплитуду ЭДС взаимной индукции ε₀₂ при различных частотах звукового генератора в интервале (5 – 50) кГц через 5 кГц.

4. По формуле (3.10) рассчитать М₂₁. Полученные данные занести в табл. 3.3.

Таблица 3.1

Uэфф=2 В, f=10 кГц
Z, см	e02	М21, Гн	e01	М12, Гн
дел	В	дел	В

Таблица 3.2

f=20 кГц
Uэфф, В	0,2	0,4	0,6	0,8	…	5,0
e02, В
М21, Гн

Таблица 3.3

Uэфф=2,5 В
f, кГц					…
e02, В
М21, Гн

Контрольные вопросы

1. Сформулируйте закон электромагнитной индукции Фарадея и правило Ленца.

2. В чем состоит явление взаимной индукции?

3. Чему равна ЭДС индукции двух контуров?

4. От чего зависит коэффициент взаимной индукции?

5. Объяснить график зависимости М₂₁ =f(Z), полученный в данной работе.

Литература:

[1] §128. [2] §25.4. [3] т.1 - §2.57. [6] §66 [4] [8]

Лабораторная работа 2-21

Изучение электрических колебаний в связанных контурах. (ФПЭ-13)

Цель работы – изучение обмена энергии в системе электрических контуров, слабо связанных между собой.

Колебательные процессы (осцилляции) в электрических контурах имеют аналоги в механике. Поведение простейшего осциллятора – одиночного маятника, представляющего собой массу, подвешенную на длинном стержне, хорошо изучено: это гармонические колебания с частотой ω₀.

Существенно более сложную структуру при колебаниях представляет собой система двух одинаковых маятников, связанных между собой слабой пружиной, как это показано на рис. 9.1. Маятники будут участвовать в коллективных колебаниях, амплитудно–частотная характеристика которых зависит от фазы смещения маятников друг относительно друга (относительная фаза).

Если оба маятника имеют вначале, при t= 0,равные смещения, то они будут колебаться как единое целое с постоянной амплитудой и частотой, равными амплитуде и частоте колебаний одиночного маятника ω₀. Если при t= 0 имеются равные амплитуды и противоположные фазы, то маятники будут колебаться с постоянной амплитудой и с частотой ω₁, слегка повышенной по отношению к ω₀. Эти два вида движения называются нормальными модами колебаний системы связанных осцилляторов, причем вид колебаний с частотой ω₀ называют четной модой нормальных колебаний и обозначают значком «+» (ω ⁺ = ω₀), а вид колебаний с повышенной частотой ω₁ называют нечетной модой нормальных колебаний и обозначают значком «-» (ω^- = ω₁). Нормальная мода колебаний – это коллективное колебание, при котором амплитуда колебаний каждой движущейся частицы системы остается неизменной. В более сложных случаях, когда при t =0 имеется относительный сдвиг фаз, результирующее движение можно рассматривать как комбинацию (суперпозицию) двух нормальных мод колебаний, как амплитудно-модулированное колебание с суперпозицией гармонических колебаний разных частот, с чем приходится встречаться в самых разнообразных явлениях. Примером могут служить не только маятники, но и два звучащих камертона с разными собственными частотами, причем наиболее интересным образом проявляются коллективные колебания, когда частоты колебаний камертонов мало отличаются друг от друга. В этом случае человеческое ухо наиболее воспринимает результирующее колебание как гармоническое колебание с переменной амплитудой, т.е. ухо слышит звук, интенсивность которого периодически меняется с частотой 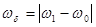и периодом 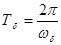. Такой вид суперпозиции гармонических колебаний (при ω₀ ≈ ω₁, но ω₁ > ω₀) иллюстрирует рис. 9.2. Само это явление называется биениями, а величины Т_δ и ω_δ –

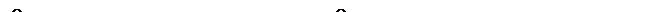периодом и частотой биений соответственно.

В системе двух связанных слабой пружиной маятников биения могут установиться, если сместить один из них (например, маятник 1, рис. 9.1), удерживая другой на месте, а затем отпустить их одновременно. В этом случае маятник 1 начинает колебаться один, но с течением времени колебания маятника 2 будут постоянно нарастать, а колебания маятника 1 – затухать. Через некоторое время маятник 2 испытывает сильные колебания, а маятник 1 останавливается.

В случае четной моды нормальных колебаний маятники движутся вместе, пружина не растянута и частота такая же, как у одиночного маятника. В случае нечетной моды колебаний пружина растянута, что увеличивает частоту этой моды колебаний. Если в какой-то момент времени смещен только один из маятников, то возникают две нормальные моды колебаний, находящиеся в определенной относительной фазе. Но поскольку частота нечетного колебания немного выше частоты четного колебания, относительная фаза изменяется в процессе коллективного колебания. Амплитуда колебаний первого маятника оказывается равной нулю, а амплитуда второго достигает максимума, когда два нормальных вида колебаний окажутся в противофазе, затем начнется увеличение амплитуды первого маятника и т.д.

Поведение связанных осцилляторов можно легко объяснить с энергетической точки зрения. При t =0 вся энергия сосредоточена в маятнике 1. В результате связи через пружину энергия постепенно передается от маятника 1 к маятнику 2 до тех пор, пока вся энергия не окажется в маятнике 2, затем, конечно, если система осцилляторов подпитывается извне энергией для компенсации затухания колебаний из-за трения и т.д., процесс обмена энергией повторяется от маятника 2 к маятнику 1 и т.д. Таким образом “биения” – процесс обмена энергией между двумя гармоническими осцилляторами, собственные частоты которых различаются мало, а при t=0 наблюдается относительный сдвиг фаз .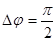

Биения можно наблюдать и в электрической схеме – в двух одинаковых LC – контурах, связанных между собой слабой емкостной связью С_в – аналогом механической связи в виде пружины. Колебания в контурах возбуждаются с помощью преобразователя импульсов (ПИ) – смотри рис. 9.3.

Дата добавления: 2015-06-04