
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Экспериментальная часть 1 страница
|
|
|
|
Приборы и оборудование
 |
Функциональная схема представлена на рис. 9.5, где:
ИП – источник питания;
ПИ – преобразователь импульсов;
PQ – звуковой генератор;
PO – осциллограф;
МЕ – магазин емкостей;
ФПЭ-13 – модуль.
Метод измерений
Для теоретических расчетов рассмотрим упрощенный вариант этой схемы – рис. 9.4, где обозначены знаки зарядов с обкладок конденсаторов в контурах и положительное направление тока: Св=С12; L1=L2=L, причем для наблюдения биений важно, чтобы I1 и I2 были сонаправлены. Для двух LC – контуров, соединенных по схеме, показанной на рис. 9.4, можно записать два уравнения, описывающих колебания зарядов Q в контурах:
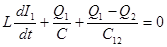 (9.1)
(9.1)
 (9.2)
(9.2)
Подставляя  ,
,  получаем:
получаем:
 (9.3)
(9.3)
 (9.4)
(9.4)
Получилось довольно сложные уравнения для двух переменных. Можно упростить ситуацию, написать новые уравнения, полученные сложением и вычитанием уравнений (9.3) и (9.4).
Сложив эти уравнения, получаем:
 (9.5)
(9.5)
Разность (9.3) и (9.4) имеет вид
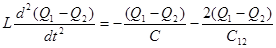 (9.6)
(9.6)
С помощью проведенных математических операций удалось свести уравнения (9.3) и (9.4) к более простым, относительно переменных (Q1+Q2) и (Q1-Q2).
Если при t =0 переменная (Q1 + Q2) имеет значение (Q1 + Q2)0, то решение уравнения (9.5) имеет вид
 (9.7)
(9.7)
частота  равна частоте собственных колебаний отдельного контура. Аналогично, решение уравнения (9.6) приобретает вид:
равна частоте собственных колебаний отдельного контура. Аналогично, решение уравнения (9.6) приобретает вид:
 (9.8)
(9.8)
где  ; (Q1 - Q2)0 – значение при t =0 переменной (Q1-Q2).
; (Q1 - Q2)0 – значение при t =0 переменной (Q1-Q2).
Два вида движения, описываемые уравнениями типа (9.7) и (9.8), называются нормальными модами колебаний системы связанных контуров. В данном случае они описывают колебания тока в системе двух связанных электрических контуров. Нормальная мода колебаний – это коллективное колебание тока, при котором амплитуда колебаний каждого заряда остается неизменной.
Если вывести из положения равновесия один из контуров, то результирующим колебанием будет колебание двух нормальных мод колебаний. При Q20=0 из (9.7) и (9.8) получаем:
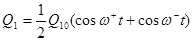 ; (13.9)
; (13.9)
 . (9.10)
. (9.10)
Используя известные тригонометрические тождества:
 ; (9.11)
; (9.11)
 ; (9.12)
; (9.12)
можно записать уравнения 9.9 и 9.10 в виде:
 ; (9.13)
; (9.13)
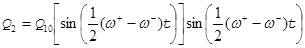 . (9.14)
. (9.14)
Вид функций Q1(t) и Q2(t) по уравнениям 9.13 и 9.14 показан на рис. 9.2. При t =0 амплитуда Q2 равна нулю. Затем амплитуда Q2 увеличивается, а амплитуда Q1 падает до тех пор, пока в момент времени, определенный из соотношения  амплитуда Q1 не станет минимальной, а амплитуда Q2 достигнет максимума.
амплитуда Q1 не станет минимальной, а амплитуда Q2 достигнет максимума.
Ситуацию, показанную на рис. 9.2, можно рассмотреть с энергетической точки зрения.
При t =0 вся энергия сосредоточена в контуре 1. В результате связи через емкость С12 энергия постепенно передается от контура 1 к контору 2 до тех пор, пока вся энергия не соберется в контуре 2. Время, необходимое для перехода энергии из контура 1 в контур 2 и обратно, можно получить из уравнения  , а частота, с которой контуры обмениваются энергией
, а частота, с которой контуры обмениваются энергией
 (9.15)
(9.15)
Для четной моды колебаний, обозначенной знаком «+», токи текут в одинаковом направлении и на емкости С12 нет заряда. При этом частота ω + остается такой же, как для несвязанных контуров, т.е.  . В случае нечетной моды нормальных колебаний (знак «–»), емкость С12 заряжена, что увеличивает частоту колебаний, т.е.
. В случае нечетной моды нормальных колебаний (знак «–»), емкость С12 заряжена, что увеличивает частоту колебаний, т.е.  .
.
Следует отметить, что для того, чтобы применить к связанным контурам рассмотренную выше теорию, они должны иметь одинаковую резонансную частоту 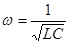 и, кроме того, предполагается, что С12 велика по сравнению с С, то есть
и, кроме того, предполагается, что С12 велика по сравнению с С, то есть  <<1 («слабая связь»). Тогда выражение 9.15 можно преобразовать следующим образом
<<1 («слабая связь»). Тогда выражение 9.15 можно преобразовать следующим образом
 (9.16)
(9.16)
Полученное значение частоты обмена ωобм (имеется в виду обмен энергией), или частоты “биений” ωбиен=ωобм можно изменять, настраивая систему контуров, путем изменения номиналов элементов С, С12, L, R и т.д., добиваясь того, чтобы разностная частота  была сведена к минимуму.
была сведена к минимуму.
Исследование биений, то есть обмена энергий в связанных контурах и является одной из практических задач данной лабораторной работы.
Экспериментальная установка
 |
Принцип работы модуля ФПЭ-13 основан на электрической связи двух одинаковых колебательных контуров LC в условиях балансировки контуров. Колебания возбуждаются с помощью генератора Г3-118. Прямоугольный импульс подается на плату ФПЭ-13. На плате ФПЭ-13 установлены два LC- контура, которые связаны внешней емкостной связью. Для отсечки источника сигнала во время паузы от первичного контура (L1C1) в цепь питания включен кремниевый диод VD1. В промежутках между прямоугольными импульсами возбуждаемые в контуре L1C1 затухающие колебания через внешнюю емкостную связь (50-80пф) передаются в контур (L2C2), где накладываются на собственные колебания. На экране осциллографа отображается периодическое возрастание и убывание амплитуды затухающих колебаний, т.е. биение колебаний (рис. 9.7).
Порядок выполнения работы
1. Ознакомиться с работой звукового генератора (в режиме генерации синусоидальных колебаний) и электронного осциллографа.
2. Подготовить приборы к работе:
а) с помощью магазина емкостей МЕ установить С =4∙10-2 мкФ;
б) установить следующие параметры выходного напряжения звукового генератора: частота – 200 Гц, величина напряжения – 2-4 В, режим работы – генерация синусоидальных колебаний;
в) включить развертку электронного осциллографа с запуском от усилителя и установить частоту развертки, удобную для наблюдения сигналов частотой 200 Гц;
г) усиление по оси У электронного осциллографа установить таким, чтобы было возможно измерить переменное напряжение до 5 В.
3. Включить лабораторный стенд и приборы. Регулировкой ручек управления на панели осциллографа добиться стабильной картины процесса «биений» в контурах.
4. Вычислить Трез для одного из контуров (резонансные частоты контуров близки) по формуле Томсона  . L=60 Гн. С=10000 пф.
. L=60 Гн. С=10000 пф.
5. Изменяя величину емкости конденсатора связи С12 на магазине емкостей от 4∙10-2 до 4∙10-1 мкФ, измерить периоды «биений». Тσ определяется следующим образом: подсчитывается количество периодов (количество максимумов), укладывающихся в одно биение (число – N) – рис. 9.7. Эта величина умножается на Трез вычисленное по формуле Томсона, то есть 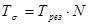 . Полученные результаты записать в табл. 9.1. По полученным таким образом значениям Тσ строится график зависимости Тσ=f(C12).
. Полученные результаты записать в табл. 9.1. По полученным таким образом значениям Тσ строится график зависимости Тσ=f(C12).
6. Провести расчет Тσ теор по  и сравнить его с экспериментальными данными.
и сравнить его с экспериментальными данными.
Таблица 9.1
| С12, мкФ | |||||||
| N | |||||||
| Тб(эксп), | |||||||
| Тб(теор), |
Контрольные вопросы
1. Как будут колебаться два связанных пружиной маятника при отсутствии сдвига фаз между ними в начальный момент?
2. Какое должно быть соотношение частот двух связанных осцилляторов для наблюдения биений?
3. Какие процессы наблюдаются в системе связанных контуров?
4. Объясните картину биений (рис. 9.2) с энергетической точки зрения.
5. Почему емкость С12 должна быть << С?
6. Покажите, что существует два максимума тока, приходящиеся на частоты нормальных мод колебаний.
7. Чему равна частота обмена энергией между двумя связанными осцилляторами?
8. Что такое нормальные колебания (моды) связанных осцилляторов?
Используемая литература
[4] §37. [3] т.1 §3.9
Библиографический список
1. Трофимова,Т.И. Курс физики: учебное пособие для вузов/ Т.И.Трофимова. –М.:Высшая школа, 1999.-542 с.,
2. Детлаф, А.А. Курс физики: учебное пособие для втузов/ А.А. Детлаф, Б.М.Яворский. – М.: Высшая школа, 2002.-718с.,
3. Лозовский, В.Н. Курс физики: учебник для вузов: в 2т./ Под ред. В.Н. Лозовского. – СПб.: Издательство “Лань”, 2000.-Т.1-676с.; Т.2.-592с.,
4. Сивухин, Д.В. Общий курс физики. Электричество/ Д.В. Сивухин. – М.:Наука, 1983.-430c.,
5. Гольдина, Л.Л. Лабораторные занятия по физике/ Под ред. Л.Л. Гольдина. – М.: Наука, 1983.-74с.,
6. Савельев, И.В. Курс общей физики. Т.2. Лабораторные занятия по физике/ И.В. Савельев. – М.:Наука, 1982.-93с.,
7. Виноградова, Ю.К. Руководство к лабораторным работам по разделу “Электричество”/ Под ред. Ю.К. Виноградова. – М.:МАИ, 1974.-125с.,
8. Бушманов, Б.Н. Физика твердого тела/ Б.Н. Бушманов, Ю.А. Хромов. – М.: Высшая школа, 1971.-732с.,
9. Виноградов, Ю.К. Электродинамика/ Ю.К. Виноградов, Н.В. Жукова, В.А. Котельников. – М.: МАИ, 1979.-329с.,
10. Лучина, А.А. Основы физики твердого тела/ А.А. Лучина. – М.:МАИ, 1979.-251с.,
Лабораторная работа 2-21
ФПЭ-09
Изучение электрических процессов в простых линейных цепях при действии гармонической электродвижущей силы.
Цель работы:
1. изучение электрических процессов в цепях, состоящих из последовательно соединенных элементов: а) двух резисторов (цепь RR), б) резистора и конденсатора (цепь RC), в) резистора и катушки индуктивности (цепь RL);
2. измерение коэффициента передачи цепей RR, RC, RL; изучение зависимости коэффициента передачи цепей RC и RL от частоты входного сигнала;
3. оценка параметров цепей R, C, L;
4. определение разности фаз между колебаниями тока в изучаемых цепях и входным напряжением.
Теоретическое введение
Цепь переменного электрического тока представляет собой ряд соединенных между собой в той или иной последовательности элементов, в которых возбуждаются токи одним или несколькими источниками ЭДС.
Все элементы электрической цепи обладают сопротивлением. Это сопротивление может бить двух видов: активное или реактивное. Если при прохождении тока через элемент происходит только необратимое превращение электрической энергии в теплоту, то его сопротивление называют активным. Если же подобной потери электрической энергии не происходит, сопротивление элемента называют реактивным.
Элемент цепи с активным сопротивлением называется резистором. Реактивным сопротивлением - емкостным и индуктивным - обладают соответственно конденсаторы и катушки индуктивности.
Элементы цепи называются идеальными, если они обладают только одним видом сопротивления - активным, емкостным или индуктивным. Для идеальных элементов справедливы соотношения:
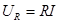
 (1)
(1)

 (2)
(2)

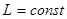 (3)
(3)
Где  - сопротивление резистора;
- сопротивление резистора;  - емкость конденсатора;
- емкость конденсатора; 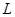 - индуктивность катушки;
- индуктивность катушки;  ,
, 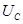 ,
, 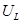 - падения напряжения (или просто напряжения) на соответствующих элементах;
- падения напряжения (или просто напряжения) на соответствующих элементах;  - ток через элемент;
- ток через элемент;  - заряд конденсатора;
- заряд конденсатора;  - ЭДС самоиндукции, возникающая в катушке индуктивности при прохождении через нее переменного тока.
- ЭДС самоиндукции, возникающая в катушке индуктивности при прохождении через нее переменного тока.
Элементы цепи могут быть линейными и нелинейными. Если сопротивление элемента не зависит от величины тока в цепи или от напряжения на элементе, то такой элемент называется линейным. Электрические цепи, составленные из линейных элементов, также называются линейными. В линейных цепях электрические процессы описываются линейными алгебраическими или дифференциальными уравнениями. Этому условию, например, отвечают выражения (1)-(3). Электрические процессы в линейных цепях называются установившимися (стационарными), если закон изменения всех токов и напряжений совпадает с точностью до постоянной величины с законом изменения внешней ЭДС, действующей в цепи. Если это условие не выполняется, процессы называются переходными.
При анализе электрических процессов в цепях переменного тока к мгновенным значениям тока можно применять законы Ома и Кирхгофа и другие правила, установленные для постоянного тока, если переменный ток является квазистационарным. Условие квазистационарности означает, что мгновенные значения переменного тока практвчески одинаковы на всех участках цепи. Это условие выполняется для медленно меняющегося тока, когда его мгновенное значение не успевает изменится за время распространения электрического процесса вдоль цепи. Если  - характерное время изменения мгновенного значения тока, а
- характерное время изменения мгновенного значения тока, а  - время распространения электрического процесса вдоль цепи протяженностью
- время распространения электрического процесса вдоль цепи протяженностью  со скоростью
со скоростью  (равной по порядку величины скорости распространения электромагнитного возмущения
(равной по порядку величины скорости распространения электромагнитного возмущения 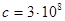 м/с), то условие квазистационарности запишется в виде
м/с), то условие квазистационарности запишется в виде  .
.
В дальнейшей будем полагать, что элемента цепи являются идеальными и, в соответствии с соотношениями (1) - (3), линейным.
Электрические процессы будем считать установившимися, а переменные токи - квазистационарными.
Рассмотрим электрическую цепь, состоящую из последовательно соединенных резистора R, емкости C и индуктивности L (рис.1). Допустим, что источник переменной ЭДС (генератор) не обладает внутренним сопротивлением 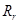 и создает на входе цепи напряжение
и создает на входе цепи напряжение 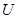 равное его ЭДС
равное его ЭДС  . Такое допущение всегда можно сделать, включив сопротивление генератора
. Такое допущение всегда можно сделать, включив сопротивление генератора 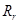 в состав рассматриваемой электрической цепи.
в состав рассматриваемой электрической цепи.

Рис. 1
Положим далее, что генератор с гармонической ЭДС
 (4)
(4)
создает в стационарном состояние в цепи ток
 (5)
(5)
где  - круговая частота колебаний ЭДС и тока;
- круговая частота колебаний ЭДС и тока;  - период колебаний;
- период колебаний; 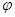 - угол сдвига фазы тока относительно фазы ЭДС;
- угол сдвига фазы тока относительно фазы ЭДС;  - амплитуда ЭДС;
- амплитуда ЭДС;  - амплитуда тока.
- амплитуда тока.
Найдем, чему равны амплитуда  и сдвиг фазы
и сдвиг фазы 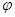 тока, если известны параметры цепи
тока, если известны параметры цепи  ,
,  ,
, 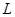 , и уравнение для ЭДС (4).
, и уравнение для ЭДС (4).
Одновременно определим, какой вид имеет величина  , равная отношению амплитуды ЭДС к амплитуде тока:
, равная отношению амплитуды ЭДС к амплитуде тока: 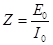 .
.
Эта величина (по аналогии с законом Ома для замкнутой цепи постоянного тока) называется полным сопротивлением цепи переменного тока. На основании второго правила Кирхгофа для контура на рис.1,а можем записать  или (рис. 1,б)
или (рис. 1,б)
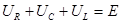 (6)
(6)
т.е. сумма напряжений на отдельных элементах контура равна в каждый момент времени внешней ЭДС, действующей в контуре.
Учитывая соотношения (1)-(3), имеем
 (7)
(7)
Подстановка в уравнение (7) выражений (4), (5) и выполнение операций интегрирования и дифференцирования приводит это уравнение к виду

Используя далее соотношения
 ,
, 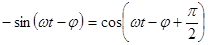
окончательно получим
 (8)
(8)
Из уравнения (8) можно сделать ряд выводов.
Выпишем из этого уравнения выражения для напряжений  ,
, 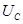 ,
, 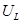 и рассмотрим их совместно с выражением (5) для тока
и рассмотрим их совместно с выражением (5) для тока  :
:
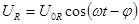 , где
, где 
 , где
, где 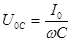 (9)
(9)
 , где
, где 
Сравнивая фазы напряжений  ,
, 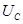 и
и 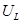 с фазой тока
с фазой тока  , видим, что:
, видим, что:
1) напряжение на резисторе  совпадает по фазе с током
совпадает по фазе с током  ;
;
2) напряжение на емкости 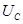 отстает по фазе от тока
отстает по фазе от тока  на угол
на угол 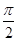 ;
;
3) напряжение на индуктивности 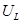 опережает по фазе ток
опережает по фазе ток  на угол
на угол 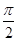 .
.
Далее найдем отношения амплитуд напряжений 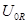 ,
,  ,
,  к амплитуде тока
к амплитуде тока  :
:
 ;
; 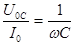 ;
;  (10)
(10)
Формулы (10) определяют величины, которые называются соответственно активным, реактивным емкостным и реактивным индуктивным сопротивлениями. Емкостное сопротивление обозначается через  , индуктивное – через
, индуктивное – через  . Из формул (10) следует, что активное сопротивление цепи переменного тока равно сопротивлению цепи для постоянного тока, т.е. омическому сопротивлению
. Из формул (10) следует, что активное сопротивление цепи переменного тока равно сопротивлению цепи для постоянного тока, т.е. омическому сопротивлению  , реактивные же сопротивления:
, реактивные же сопротивления:
 ;
; 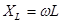 (11)
(11)
Перейдем к основной задаче: нахождению выражений, определяющих амплитуду тока  , сдвиг по фазе
, сдвиг по фазе 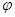 тока относительно ЭДС и полное сопротивление
тока относительно ЭДС и полное сопротивление  цепи, изображенной на рис. 1.
цепи, изображенной на рис. 1.
Уравнение (8) позволяет решить эту задачу, при этом методы решения могут быть различные. Воспользуемся графическим способом представления гармонических колебаний - методом векторных диаграмм. В этом методе гармоническим величинам (напряжениям, токам) сопоставляются вращающиеся векторы. Для этого на плоскости выбирают произвольное начало координат 0 и проводят ось X. Изучаемую гармоническую величину изображают вектором, построенным из начала координат. Длина вектора разка (в выбранном масштабе) амплитуде гармонической величины, а угол между вектором и осью X равен углу начальной фазы. Вектор равномерно вращается вокруг точки 0 с угловой, скоростью 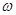 в направлении против часовой стрелки. При этом проекция вектора на ось Х в любой момент времени равна мгновенному значению гармонической величины, изменяющейся со временем по закону косинуса.
в направлении против часовой стрелки. При этом проекция вектора на ось Х в любой момент времени равна мгновенному значению гармонической величины, изменяющейся со временем по закону косинуса.
В соответствии со сказанным левую часть уравнения (8) можно рассматривать как сумму проекций векторов, изображающих напряжения  ,
, 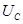 и
и 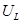 , а правую часть - как проекцию вектора, изображающего суммарное напряжение
, а правую часть - как проекцию вектора, изображающего суммарное напряжение  . Поскольку при сложении векторов сумма проекций слагаемых равна проекции суммы, то можно найти геометрическую сумму векторов, изображающих напряжения
. Поскольку при сложении векторов сумма проекций слагаемых равна проекции суммы, то можно найти геометрическую сумму векторов, изображающих напряжения  ,
, 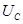 ,
, 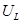 и приравнять эту геометрическую сумму вектору, изображающему напряжение
и приравнять эту геометрическую сумму вектору, изображающему напряжение  . Другими словами, вместо алгебраического равенства (8) можно рассматривать векторное равенство
. Другими словами, вместо алгебраического равенства (8) можно рассматривать векторное равенство
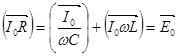 (12)
(12)
что значительно упрощает нахождение амплитуды  и сдвига фаз
и сдвига фаз 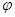 . На рис. 2, а, б построены векторные диаграммы для момента времени t=0, соответствующие уравнениям (8) и (12).
. На рис. 2, а, б построены векторные диаграммы для момента времени t=0, соответствующие уравнениям (8) и (12).

Из рис. 2,6 следуют соотношения:
 ;
; 
откуда
 (13)
(13)
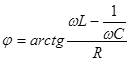 (14)
(14)
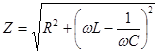 (15)
(15)
Видим, что колебания тока в цепи отстают по фазе от колебаний ЭДС на угол 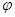 , зависящий от частоты и определяемый согласно (14). Можно также сказать, что напряжение
, зависящий от частоты и определяемый согласно (14). Можно также сказать, что напряжение 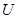 во внешней цепи, содержащей последовательно соединенные
во внешней цепи, содержащей последовательно соединенные  ,
,  и
и 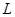 , опережает по фазе ток на угол
, опережает по фазе ток на угол 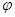 , определяемый выражением (14). Полное сопротивление цепи
, определяемый выражением (14). Полное сопротивление цепи  , в соответствии с (15), также зависит от частоты и может быть записано в виде
, в соответствии с (15), также зависит от частоты и может быть записано в виде
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 746; Нарушение авторских прав?; Мы поможем в написании вашей работы!