Решение. Условия для электростатического поля на границе раздела изотропных диэлектрических сред

Условия для электростатического поля на границе раздела изотропных диэлектрических сред

Теорема Гаусса для электростатического поля в среде

Электрическим смещением называется векторная величина 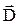, характеризующая электрическое поле:

.

,

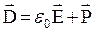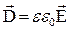где e = (1+k) - относительная диэлектрическая проницаемость диэлектрика, безразмерная физическая величина, показывающая, во сколько раз электрическое поле в диэлектрике меньше, чем в отсутствие диэлектрика.

e = Е _о / Е.

Теорема Гаусса для электростатического поля в среде: Поток вектора электрического смещения через произвольную замкнутую поверхность равен свободному электрическому заряду, попавшему внутрь этой поверхности:

.

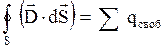1. Составляющая вектора напряженности, параллельная границе раздела диэлектриков (тангенциальная составляющая), не изменяется при переходе через границу раздела диэлектриков:

E_2t = E_1t и D _2t / D _1t = e ₂ / e ₁.

2. Разность нормальных составляющих вектора электрического смещения на границе раздела диэлектриков равна поверхностной плотности свободных электрических зарядов на границе раздела:

D_1n - D_2n= s _своб и e₁ Е_1n - e₂ E_2n= s _своб /e _о.

Р _1n - P _2n = s _связ.

Если s _своб = 0, то e₂ E _2n = e₁Е _1n и D _n2 = D _1n.

Примеры решения задач

Пример 1. Диагонали ромба имеют длину d₁ = 2 см, d₂ = 3 см. На концах короткой диагонали расположены заряды q₁ = 2 нКл, q₂ = 6 нКл; на концах длинной - заряды q₃ = 3 нКл, q₄ = 12 нКл. Определить модуль вектора напряженности электрического поля в центре ромба и угол между вектором напряженности и короткой диагональю.

Рис.1.5

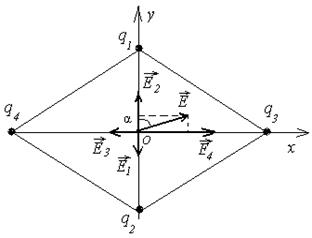
Так как электрическое поле создано несколькими зарядами, то для нахождения его напряженности надо применить принцип суперпозиции. Напряженность результирующего поля равна векторной сумме напряженностей полей, созданных каждым зарядом в отдельности:

.

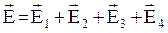Направления векторов показаны на рис.1.5. Модули составляющих векторов можно найти по формуле напряженности поля точечного заряда:

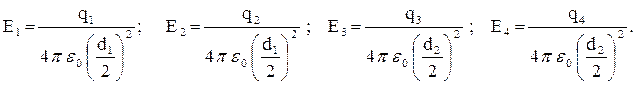
Чтобы сложить вектора, выберем координатные оси х и у, как показано на рисунке, и найдем проекции результирующего вектора E_x и E_y как суммы проекций всех составляющих векторов на эти оси координат:

Здесь Е_1х = - Е₁, Е_2х = Е₂, Е_3х = 0, Е_4х = 0,

Е_1у = 0, Е_2у = 0, Е_3у = - Е₃, Е_4у = Е₄.

Тогда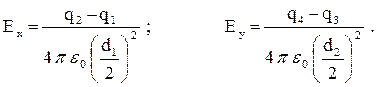

Вычислим проекции вектора :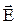

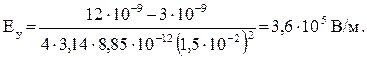
Модуль результирующего вектора Е найдем через его проекции на оси координат:

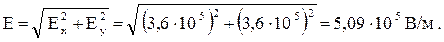
Найдем теперь угол, который вектор 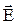образует с короткой диагональю ромба. Из рисунка видно, что 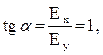значит a = 45^о.

Ответ: Е = 5,09×10⁵ В/м, a = 45^о.

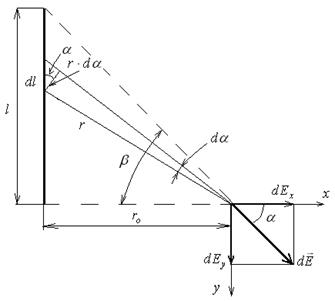Пример 2. Тонкий стержень длиной l = 10 см заряжен с линейной плотностью t = 400 нКл/м. Найти напряженность электрического поля в точке, расположенной на перпендикуляре к стержню, проведенном через один из его концов, на расстоянии r₀ = 8 см от его конца.

Рис.1.6

Решение

Применим принцип суперпозиции для поля непрерывно распределенных зарядов:

.

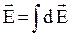Выделим на стержне бесконечно малый участок длиной d l (рис.1.6) Находящийся на нем заряд 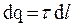можно считать точечным, и напряженность поля, созданного им, рассчитывать как

.

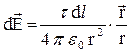Из приведенного рисунка видно, что

Следует иметь в виду, что 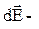вектор, поэтому прежде чем интегрировать, выберем оси координат х и y и найдем проекции вектора 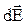на эти оси:

,

или, учитывая сделанные подстановки,

Интегрируя эти выражения в пределах от 0 до b (рис. 1.6.), получим:

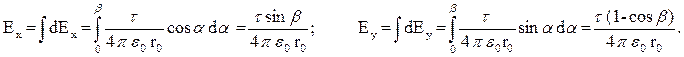
где Е_х и Е_у – проекции результирующего вектора 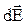на оси х и у.

Подставим числовые значения заданных величин в системе СИ и произведем вычисления:

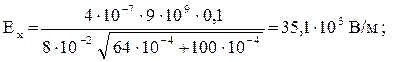
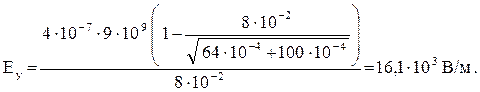
Вектор напряженности определится через проекции Е_х и Е_у:

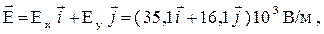
где 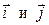– орты координатных осей х и у.

Модуль вектора напряженности найдем через его проекции на оси координат:

.

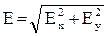Вычислим: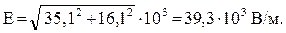

Ответ: Е = 39,3×10³ В/м.

Пример 3. Тонкие стержни образуют квадрат со стороной l. Стержни заряжены с линейной плотностью t = 1,33 нКл/м. Найти потенциал j в центре квадрата.

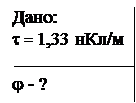
Дата добавления: 2015-06-04