Расчет интерференционной картины от двух источников

ИНТЕРФЕРЕНЦИЯ

ЛЕКЦИЯ 4.

Расчет интерференционной картины от двух источников. Интерференция света в тонких пленках. Полосы равного наклона (интерференция от плоскопараллельной пластинки). Полосы равной толщины (интерференция от пластинки переменной толщины). Кольца Ньютона. Применение интерференции света

Расчет интерференционной картины для рассмотренных выше методов наблюдения интерференции света можно провести, используя две узкие параллельные щели, расположенные достаточно близко друг к другу (рис. 4.1). Щели S₁ и S₂ находятся на расстоянии d друг от друга и являются когерентными (реальными или мнимыми изображениями источника в ка­кой-то оптической системе) источниками света.

Рис.4.1. К расчету интерференционной картины от двух параллельных щелевых источников.

Интерференция наблюдается в произ­вольной точке Р экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l>>d. Начало отсчета выбрано в точке О, симметричной относительно щелей.

Интенсивность в любой точке P экрана, лежащей на расстоянии x от О, определяется оптической разностью хода D = s₂ – s₁. Из рис. 4.1 имеем

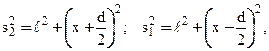
откуда 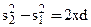, или

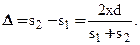
Из условия 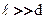следует, что s₁ + s₂» 2 l,поэтому

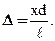(4.1)

Подставив найденное значение D (4.1) в условия (3.2) и (3.3), получим, что максимумы интенсивности будут наблюдаться в случае, если

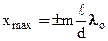(m = 0,1,2,...), (4.2)

а минимумы – в случае, если

(m = 0,1, 2,...). (4.3)

Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы, равно

(4.4)

Dх не зависит от порядка интерференции (величины m) и является постоянной для данных 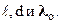Согласно формуле (4.4), Dx обратно пропорционально d; следовательно, при большом расстоянии между источниками, например при , отдельные полосы становятся неразличимыми. Для видимого света l _o» 10^{-7 м, поэтому четкая, доступная для визуального наблюдения интерференционная картина, имеет место при 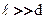(это условие и принималось при расчете). По измеренным значениям используя (4.3.), можно экспериментально определить длину волны света. Из выражений (4.2) и (4.3.) следует, таким образом, что интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование равноотстоящих светлых и темных полос, параллельных друг другу. Главный максимум, соответствующий} m = 0, проходит через точку О. Вверх и вниз от него на равных расстояниях друг от друга располагаются максимумы (минимумы) первого (m = 1), второго (m = 2) порядков и т. д.

Описанная картина, однако, справедлива лишь при освещении монохроматическим светом (l _o = const). Если использовать белый свет, представляющий собой непрерывный набор длин волн от 0,39мкм (фиолетовая граница спектра) до 0,75мкм (красная граница спектра), то интерференционные максимумы для каждой длины волны будут, согласно формуле (4.2), смещены друг относительно друга и иметь вид радужных полос. Только для m = 0 максимумы всех длин волн совпадают, и в середине экрана будет наблюдаться белая полоса, по обе стороны которой симметрично расположатся спектрально окрашенные полосы максимумов первого, второго порядков и т. д. (ближе к белой полосе будут находиться зоны фиолетового цвета, дальше - зоны красного цвета). Но спектры более высокого, чем второй порядка, начнут накладываться друг на друга и правильное чередование цветов – фиолетовый – синий – голубой – зеленый – желтый – оранжевый – красный – будет нарушено.

Дата добавления: 2015-06-04