Аксонометрические проекции

2.3.1 Общие сведения

Сущность аксонометрического проецирования заключается в том, что данный предмет вместе с осями координат параллельно проецируется на одну лишь плоскость проекции (картинная плоскость). При этом направление проецирования (указано стрелкой S) не параллельно ни одной из координатных плоскостей.

В результате проецирования предмет подвергается некоторому искажению. Отношение длины отрезков аксонометрических координат х, у и z к соответствующей длине пространственных координат (отрезков) называют показателями (или коэффициентами) искажений по аксонометрическим осям.

Принимая различное положение картинной плоскости и задавая разные направления проецирования, можно получить множество аксонометрических проекций, отличающихся величиной коэффициентов искажения. Справедливость этого утверждения была доказана немецким геометром Польке, теорема которого утверждает, что: три отрезка произвольной длины, лежащих в одной плоскости и выходящих из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на прямоугольных осях координат от начала.

Рисунок 2.8 – Пример выполнения построения трех видов по данному наглядному изображению

На основании этой теоремы аксонометрические оси и коэффициенты искажения по ним могут выбираться произвольно. В зависимости от соотношения между коэффициентами искажения различают три вида аксонометрических проекций:

1) если все три коэффициента искажения равны между собой, т.е.

k_Х0= k_У0= k_Z0 – аксонометрия называется изометрией;

2) если два из трех коэффициентов одинаковы (например k_Х0= k_У0), то такая аксонометрия называется диметрией;

3) если все три коэффициента имеют разные значения, т.е. k_Х0≠ k_У0≠ k_Z0, то такая аксонометрия называется триметрией.

Если направление проецирования S перпендикулярно к картинной плоскости, то аксонометрическое проецирование называют прямоугольным, если же проецирующие лучи наклонены к плоскости, то проецирование называется косоугольным.

2.3.2 Диметрическая проекция

При построении этой проекции ось z⁰ располагают вертикально. Ось x⁰ располагают под углом 7º10', а ось y⁰ – под углом 41º25' к горизонтали (рисунок 2.9). Приближенно аксонометрические оси стандартной диметрии можно построить, если принять tg 7º10'≈1/8, tg 41º25'≈7/8.

Рисунок 2.9 – Расположение осей в диметрической проекции

Диметрическую проекцию, как и изометрию, выполняют без искажения по осям x⁰, z⁰ и с искажением k_yo=05 по оси y⁰. Увеличение линейных размеров изображения по сравнению с действительными происходит в 1,06 раза

2.3.3 Изометрическая проекции

Для этой проекции справедливо утверждение: коэффициенты искажения по аксонометрическим осям одинаковы и равны косинусам углов наклона координатных осей к картинной плоскости (рисунок 2.10).

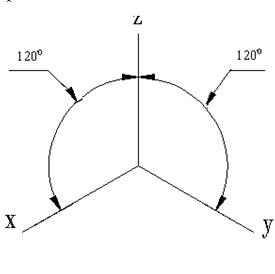
Рисунок 2.10 - Расположение осей в изометрии

Коэффициенты искажения по осям x⁰, y⁰, и z⁰ равны 0,82. Однако на практике изометрическую проекцию выполняют без искажения (т.е. k_иск=1), что соответствует увеличению линейных размеров изображения по сравнению с действительными в 1,22 раза. Ось z⁰ обычно принимают вертикальной, остальные располагают под углом 120º к ней.

Как правило, наибольшую сложность при выполнении изометрической проекции вызывают построения окружностей. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы. Большая ось эллипсов равна 1,22, а малая – 0,71 диаметра окружности.

Большие оси эллипсов расположены под углом 90⁰ к той оси, которая в данной плоскости отсутствует. Например, в плоскости XOY перпендикулярно оси Z, в плоскости XOZ – оси Y, в плоскости ZOY – оси X. (рисунок 2.11). Малые оси эллипсов расположены параллельно отсутствующим в данной плоскости аксонометрическим осям, т. е. перпендикулярно большим осям эллипсов.

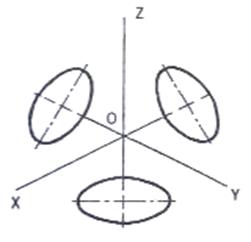
Рисунок 2.11 - Расположение эллипсов в изометрии

Построение эллипса можно выполнять в следующей последовательности: из точки О описывают две окружности диаметрами, равными осям эллипса, т.е. диаметр большой окружности будет равен 1,22*D_окр, а диаметр малой – 0,70* D_окр (рисунок 2.12). Отмечают точки О₁,О₂, О₃, О₄ – центры сопряженных дуг окружностей.

Рисунок 2.12 – Построение эллипсов в изометрии

Задание:

- построить три изображения предмета по его описанию;

- построить аксонометрическую проекцию предмета;

- выпонить простые разрезы и нанести размеры.

Рекомендации к выполнению. По описанию, данному в таблицах 2.2, 2.3, построить три изображения и аксонометрическую проекцию предмета. Предмет изобразить с двумя отверстиями – призматическим и цилиндрическим. Призматическое отверстие для всех вариантов одно и то же – это сквозное отверстие, ребра которого перпендикулярны фронтальной плоскости проекций; форму и размеры отверстия взять из таблицы 2.3. Цилиндрическое отверстие для задания выбрать в соответствии со своим вариантом из таблицы 2.2.

Выполнение задания требует мысленного представления предмета. Внимательно прочитав описание внешней формы предмета, следует представить этот предмет в пространстве. Затем мысленно выполнить в этом предмете два отверстия, данные в описании. После того, как будет уяснена конструкция предмета, следует приступать к выполнению чертежа.

Построив три вида внешней формы предмета, рекомендуется выполнить на главном виде призматическое отверстие по форме и размерам, данным в таблице 2.3. Затем построить проекции этого отверстия на виде сверху и виде сбоку. После этого построить проекции цилиндрического отверстия, начав построение с вида сверху. Построение выполнять тонкими линиями (s/3), применяя штриховые линии для невидимого внутреннего контура предмета.

После построения трех видов нужно выполнить разрезы. При заданных формах предмета потребуется выполнить три разреза: горизонтальный, фронтальный и профильный. Правила обозначения и изображения разрезов должны соответствовать ГОСТу 2.305-68. При симметричных изображениях следует обязательно соединить половину разреза с половиной вида.

После построения трех изображений предмета необходимо нанести размеры в соответствии с ГОСТ 2.307-68. Обратите внимание на то, что ни один из размеров одного изображения не должен повториться на других изображениях. За основу нанесения размеров нужно взять параметры геометрических поверхностей.

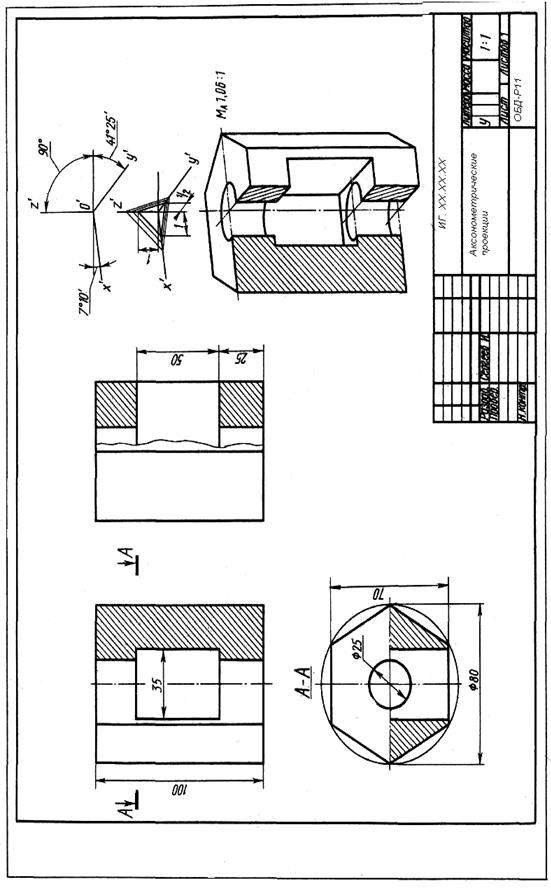
Заключительным этапом при выполнении графической работы является построение аксонометрической проекции предмета с вырезом одной четверти по ГОСТу 2.317-68. Построение начинают с проведения аксонометрических осей и изображения плоской фигуры основания, затем строят основные контуры детали, наносят линии уступов, углублений, выполняют отверстия в детали, показывают разрезы, обводят линии видимого контура до требуемой толщины (рисунок 2.13.).

Пример выполнения графической работы дан на рисунке 2.14.

Рисунок 2.13 – Построение аксонометрической проекции

Т а б л и ц а 2.2 - Описание предмета к заданию

«Аксонометрические проекции»

Вариант	Внешняя форма предмета	Цилиндрическое отверстие
1,19,28	Шестиугольная правильная призма. Диаметр окружности, описанной вокруг шестиугольника основания, равен 90 мм. Две вершины основания лежат на горизонтальной оси симметрии. Высота призмы 100 мм.	Сквозное отверстие с вертикально расположенной осью, проходящей через центр шестиугольника. Диаметр отверстия 30 мм.
2,18,29	Пятиугольная правильная призма.Пятиугольник основания вписан в окружность диаметром 90 мм. Одна из вершин пятиугольника лежит на вертикальной оси симметрии основания и является ближайшей к глазу наблюдателя. Высота призмы 100 мм.	Диаметр отверстия 30 мм. Вертикально расположенная ось проходит через центр пятиугольника.
3,17,25	Четырехугольная правильная призма. Сторона основания квадрата 70 мм.Вершины квадрата лежат на горизонтальной и вертикальной осях симметрии основания. Высота призмы 100 мм.	Диаметр отверстия 25 мм. Вертикально расположенная ось проходит через центр квадрата.
4,16,24	Прямой круговой цилиндр. Диаметр основания 90 мм. Высота цилиндра 100 мм.	Вертикально расположенное отверстие диаметром 25 мм. проходит до верхней плоскости призматического отверстия.
5,15,23	Сфера диаметром 100 мм. На высоте 30 мм. От экватора сфера срезана горизонтальной плоскостью.	Сквозное отверстие диаметром 30 мм. Ось отверстия совпадает с вертикальной осью сферы.

Продолжение таблицы 2.2

6,14,22	Четырехугольная правильная призма. Сторона квадрата основания 70 мм. Вершины квадрата лежат на горизонтальной и вертикальной осях симметрии основания. Высота призмы 100 мм.	Сквозное отверстие диаметром 30 мм. Вертикально расположенная ось отверстия проходит через центр квадрата
7,13,21	Шестиугольная правильная призма. Диаметр окружности в шестиугольник основания, равен 80 мм. Две вершины основания лежат на вертикальной оси симметрии. Высота призмы 100 мм.	Сквозное отверстие диаметром 25 мм. Вертикально расположенная ось отверстия проходит через центр шестиугольника.
8,12,20	Сфера диаметром 100 мм. На уровне 30 мм. под экватором сфера срезана горизонтальной плоскостью.	Сквозное отверстие диаметром 25 мм. Ось отверстия совпадает с вертикальной осью сферы.
9,11,26	Пятиугольная правильная призма. Пятиугольник основания вписан в окружность диаметром 90 мм. Одна из вершин пятиугольника лежит на вертикальной оси симметрии основания и является ближайшей к глазу наблюдателя. Высота призмы 100 мм.	Сквозное отверстие диаметром 25 мм. Вертикально расположенная ось проходит через центр пятиугольника.
10,27,30	Прямой круговой цилиндр Диаметром 90 мм. Высота цилиндра100 мм.	Вертикально расположенное отверстие диаметром 30 мм. До верхней плоскости призматического отверстия.

Т а б л и ц а 2.3 - Данные к заданию «Аксонометрические проекции»

Вариант	Размеры отверстия и расположение его от нижнего основания предмета (или центра сферы) мм	Форма призматического отверстия
1,9,11	а=35 b=60 z=20	а     b   z
19,26, 30	а=40 b=50 z=30
2,18, 28	а1=30 а2=40 b=50 z=30	а1     b а2 z
3,17,25	а1=35 а2=45 b=50 z=25
4,24,29	а=40 b=50 z=30	а     b     z
10,16,27	а=30 b=50 z=25
5,15,23	а=40 b=40 z=20	а     b z
8,12,20	а=35 b=35 z=17.5
6,14,24	а1=40 а2=50 b=50 z=30	а1   b   а2 z
7,13,21	а1=45 а2=35 b=50 z=25

Дата добавления: 2015-06-29