Пересечение плоскостей

Задание:

- построить проекции двух треугольников;

- определить видимость;

- построить линию пересечения треугольников;

- натуральную величину треугольника АВС.

Рекомендации к выполнению. В левой половине листа формата А₃ намечаются оси координат и из таблицы 2.4 согласно своему варианту берутся координаты точек А, В, С, D, Е, F вершин треугольника (рисунок 2.15). По координатам (x,у) строим горизонтальные проекции, а по координатам (x,z) – фронтальные проекции треугольников АВС и DEF.

Для построения линии пересечения двух плоскостей необходимо определить две точки, которые будут принадлежать обеим плоскостям.

Чтобы определить стороны, участвующие в пересечении, необходимо проанализировать их видимость по конкурирующим точкам (1 2, 3 4), потому что пары сторон треугольников представляют в пространстве скрещивающиеся прямые.

Проанализируем видимость стороны АС треугольника АВС на плоскости П₁. В точке 1 АС будет видима, так как точка ближе расположена к наблюдателю, а в точке 2 – невидима. Следовательно, прямая АС участвует в пересечении с плоскостью DEF, следовательно, есть общая точка. Для того чтобы ее найти заключаем АС во вспомогательную фронтально-проецирующую плоскость

АС 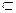, 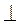П₁ → А^׳С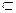^׳ f₀

Находим линию пересечения плоскостей – заданной треугольником DEF и вспомогательной (∆DEF ). На пересечении заданной прямой АС и полученной линии пересечения находим искомую точку К.

Аналогично проанализировав видимость стороны DF треугольника DEF на плоскости П₂, получим, что в точке 2 она видима, а в точке 1 – невидима, следовательно, прямая DF участвует в пересечении с плоскостью треугольника АВС.

Чтобы найти точку пересечения DF с треугольником АВС, заключаем эту прямую во вспомогательную фронтально-проецирующую плоскость .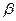

Таким образом, получаем

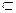
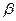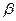
DF , 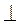П₂→ D^"F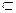^" f₀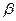

Определяем линию пересечения заданной плоскости треугольника DEF и вспомогательной плоскости 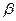. На пересечении прямой DF и полученной линии пересечения находим искомую точку М.

Соединив полученные точки М и К получим линию пересечения треугольников АВС и DEF (рисунок 2.15).

2.2.2. Определение натуральной величины треугольника АВС

Чтобы определить натуральную величину треугольника АВС необходимо плоскопараллельным перемещением привести треугольник в положение проецирующей плоскости. Для этого в треугольнике АВС из точки С строим горизонталь, а затем на чистом поле листа располагаем ее горизонтальную проекцию перпендикулярно к П₂ (рисунок 2.15). В этом случае и треугольник, содержащий эту горизонталь будет перпендикулярным к плоскости П₂, а следовательно, его фронтальная проекция превратиться в прямую линию. При таком повороте принимается ось вращения, перпендикулярная П₁. Из этого следует, что горизонтальная проекция треугольника сохраняет свой вид и величину (А₁В₁С₁=АВС) изменяется лишь ее положение. Фронтальные проекции А₁В₁С₁ находятся на соответствующих линиях связи.

При втором повороте необходимо треугольник привести в положение параллельное П₁, это возможно когда ось вращения перпендикулярна к П₂. В этом случае фронтальная проекция треугольника при повороте сохраняет свой вид и величину А₂ "В₂" С₂ ", точки А и С перемещаются в плоскостях параллельно П₂. Горизонтальные проекции треугольника находятся по соответствующим линиям связи. Проекция А₂ 'В₂ ' С₂ ' определяет натуральную величину и вид треугольника АВС.

Т а б л и ц а 2.4 – Данные к заданию на пересечение плоскостей

Номер варианта

Xa

Ya

Za

Xb

Yb

Zb

Xc

Yc

Zc

Xd

Yd

Zd

Xe

Ye

Ze

Xk

Yk

Zk

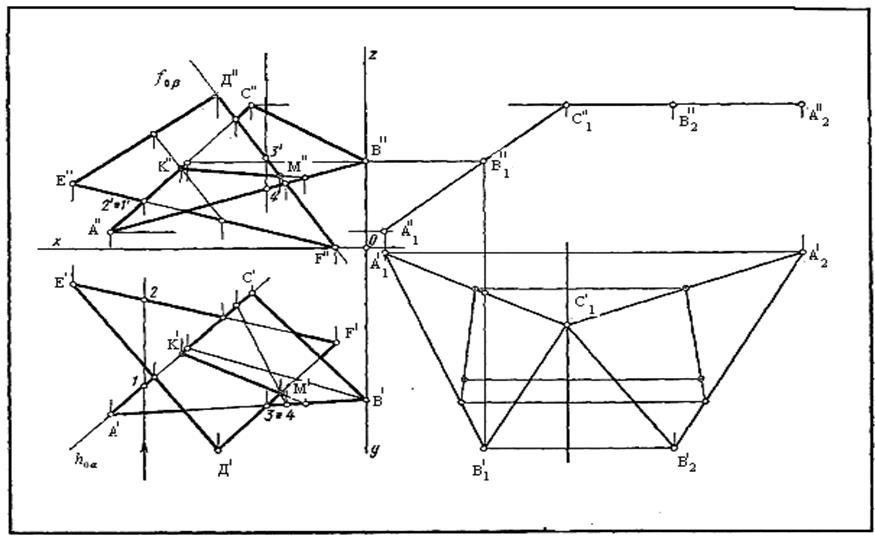
Рисунок 2.15 - Пример выполнения задания на пересечение плоскостей

Дата добавления: 2015-06-29