Продольный изгиб

Общие положения

Расчёты на устойчивость

Выше отмечалось, что в сопротивлении материалов рассматривается три вида расчётов: 1) на прочность, 2) на жесткость и 3) на устойчивость.

При рассмотрении напряженно-деформированных состояний растяжения-сжатия, кручения и изгиба решались задачи только по расчётам на прочность и жесткость.

Расчеты на устойчивость в силу их специфики приходятся выделять отдельной темой. Например, что будет показано ниже, при расчётах на устойчивость сжатого стержня необходимо рассматривать одновременно вопросы как сжатия, так и изгиба.

В предыдущих разделах, используя метод сечений для определения внутренних силовых факторов, мы рассматриваем условия статического равновесия отсеченной части стержня. При этом предполагалось, что эта отсеченная часть находится в состоянии устойчивого равновесия. Между тем, в аналитической механике рассматривается три вида равновесия: устойчивое, безразличное и неустойчивое.

Некоторые конструкции, как, например, длинные тонкие стержни, испытывающие сжатие вдоль оси; труба под действием наружной распределенной нагрузки; оболочки под действием сосредоточенной нагрузки при некоторых значениях нагрузки могут перейти из заданного положения равновесия в состояние неустойчивого равновесия. Соответствующие нагрузки получили название критических.

В сопротивлении материалов в качестве примера перехода из состояния устойчивого равновесия в неустойчивое рассматривается сжатие гибкого стержня.

При продольном сжатии стержня может наступить такой момент, когда прямоугольный стержень при разовом воздействии поперечного толчка изогнётся. Такое состояние, когда стержень может иметь как прямолинейную ось, так и изогнутую, получило название «бифуркация». Сжимающая сила, соответствующая такому состоянию, получила название критической силы «Р кр». Задачу по определению критической силы сжатого стержня впервые решил Леонард Эйлер, решая задачу продольного изгиба.

При решении задачи по расчёту длинного тонкого стержня на продольный изгиб Эйлер предполагал, что стержень выполнен из линейно-упругого материала.

Расположим шарнирно опертый стержень в горизонтальном положении, см. рис 12.1. Правый торец стержня опирается на «каток», левый – на неподвижную шарнирную опору.

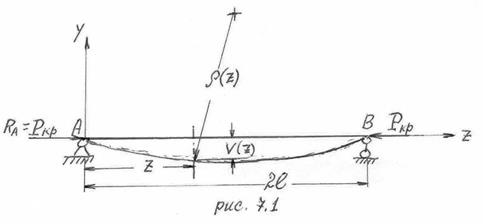
При действии в сечении «В» критической силы «Р кр» стержень получит боковое выпучивание. Перемещением подвижного шарнира «В» пренебрегаем, считая, что длина стержня 2l остается неизменной. Стержень работает на изгиб. Сечению «Z» соответствует прогиб «V» и кривизна «ρ». Выше было получено выражение для кривизны балки:

В случае потери устойчивости стержень всегда прогибается в плоскости наименьшей жесткости. Поэтому момент инерции не зависимо от обозначения осей при расчете стержней на устойчивость принято обозначать «J min». Дифференциальное уравнение упругой линии балки при продольном изгибе записывается следующим образом:

(12.1)

Или:

Дифференциальное уравнение упругой линии балки при продольном изгибе записывается следующим образом:

(12.2)

Прогиб «V» мал, то есть:

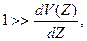
И знаменатель левой части уравнения (12.1) можем считать равным единице.

Изгибающий момент может быть определен:

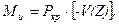
В итоге получаем:

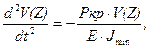
И окончательно дифференциальное уравнение при продольном изгибе получает вид:

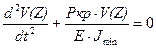(12.3)

Введем обозначение:

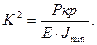(12.4)

Тогда:

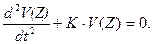(12.5)

Решение уравнения (12.5) ищем в виде:

(12.6)

Постоянные интегрирования определим из граничных условий:

1) При Z=0, V(A) = 0;

2) При Z=l, V(B) = 0

В итоге решение уравнения (7.5) имеет вид:

V(Z)=A·sin Kl = 0

Для определения критической силы рассмотрим выражение (12…..). Значение, равное нулю, синус принимает при следующих значениях аргумента:

Kl= O; π;2π;…;nπ.

Минимальное значение аргумента получает вид:

Kl=π

Или:

С учётом (12.4) можем записать:

Окончательно, полученное Л.Эйлером выражение для критической силы имеет вид:

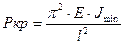(12.7)

Согласно (12.7) данное значение критической силы имеет место, когда стержень получает прогиб по полусинусоиде. Но это справедливо только для рассматриваемого случая закрепления стержня. Например, при трёх опорах стержень получает прогиб равный одному периоду синусоиды (см. рис. 12.2).

Дата добавления: 2015-06-30