Расчёт равномерно вращающегося стержня

Рассмотрим стержень, равномерно вращающийся вокруг оси «Y», см.рис 17.3.Длина стержня «L»,площадь

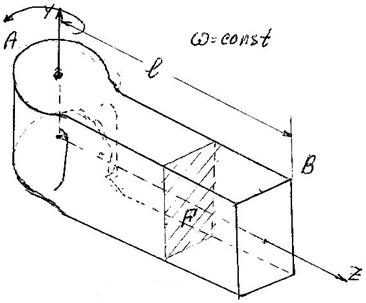
Рис. 17.3

поперечного сечения «F». При расчёте стержня собственной массой стержня пренебрегаем. Так как будем учитывать только инерционную нагрузку, то для простоты обозначений индексы «ин» везде опустим. Модуль окружной скорости при равномерном вращении постоянен, но вследствие непрерывного изменения направления вектора, движение является ускоренным.

Силы инерции зависят от величины угловой скорости «» и от радиуса вращения. В каждом сечении по толщине стержня силы инерции одинаковы. Поэтому в качестве расчётной схемы можем принять плоский стержень, см. рис. 17.4. Применяя принцип Даламбера мы как бы останавливаем вращательное движение. Поэтому в расчётной схеме ось вращения может быть представлена в виде жёсткого закрепления.

Рис. 17.4

Силы инерции направлены от оси вращения. Так как от сечения к сечению силы инерции меняются, необходимо перейти к интенсивности сил инерции «q»,см.рис.17.4:

Определим элементарную центробежную силу инерции на текущем расстоянии «Z» от оси вращения:

= dm

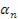
Элементарная масса элемента стержня длиной «dz»:

,

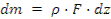Где 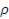- удельная масса материала стержня. Центростремительное ускорение на радиусе «z»:

=

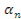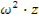
Тогда:

И интенсивность центробежной силы:

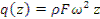
Зависимость оn «z»линейная, строим эпюру «q(z)»,см. рис. 17.4.

Максимальное значение интенсивности центробежной силы будет:

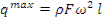
Для определения внутреннего силового фактора применим метод плоских сечений. Проводим плоскость на расстоянии «z» от сечения «A» и рассматриваем правую часть стержня, см.рис. 17.5

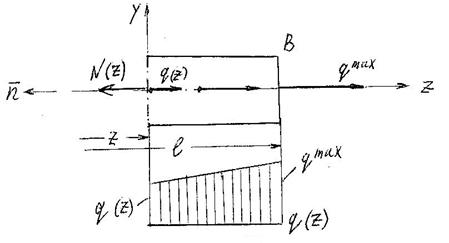
Рис. 17.5.

Из расчётной схемы на рис. 17.5 следует, что от действия центробежных сил инерции возникнет нормальная сила N(z). Уравнение равновесия запишется в следующем виде:

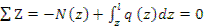
Тогда: ,

Или: .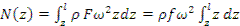

Окончательно: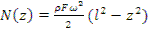

В сечении «А», то есть на оси вращения, при «Z=0» будет действовать максимальная нормальная сила:

На конечном торце стержня в сечении «B» при «z=l»: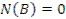

Эпюра N(z) параболическая, так как «z» во второй степени. При этом, вершина параболы находиться в сечении «А», так как в этом сечении «», а интенсивность есть первая производная о силы инерции. Максимальное напряжение на оси вращения:

,

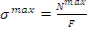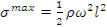
Тогда связь с линейной скоростью: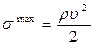

Из полученного результата следует, что величина напряжения не зависит от площади сечения стержня. С увеличением площади пропорционально увеличивается масса стержня и соответствующие силы инерции. Поэтому при расчёте вращающихся элементов конструкции на прочность лимитирующим фактором оказывается окружная скорость вращения. Расчёты ведутся по допускаемому числу оборотов.

Уравнение прочности: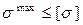

Тогда, согласно последнему равенству можем записать в нашем случае для допускаемой окружной скорости: .

Учитывая, что

Окончательно получим:

Где [ ]- допускаемая угловая скорость,

[n]- допускаемое число оборотов в минуту.

Пример

Плоская рама вращается вокруг участка «АВ» с постоянной угловой скоростью «ω». Все участки рамы имеют круглое сечение диаметра «D». В точке «С» расположена сосредоточенная масса. Собственным весом рамы пренебречь.

Требуется:

1) Изобразить схему нагружения рамы силами инерции;

2) Построить эпюру изгибающих моментов М_х(z);

3) Найти положение плоского сечения и из условия прочности определить допускаемое число оборотов в минуту n.

Данные к задаче:

l=1 м; D=0,02 м; ρ=7,8 m/м³; [σ]=160 МПа,

Схема рамы предоставлена на рис. 17.6

Рис. 17.6

Решение.

1. Схема нагружения

Считаем, что подшипник в сечении «А» помимо вертикальных нагрузок может воспринимать и осевые нагрузки. Значит, опору в сечении «А» можем считать шарниром, тогда в сечении «В» будет каток.

Характерные сечения обозначаем начальными буквами латинского алфавита, см. рис. 17.7.

На участках АL и LB силами инерции можно пренебречь по сравнению с участками CE и EL, так как силы инерции на радиусе 0,01 м весьма малы по сравнению с силами на радиусе 1м.

Поэтому считаем что участки «AL» и «LB» силами инерции не нагружены.

Рис. 17.7

В сечении «С» приложена сосредоточенная масса m=2 кг, которая создает силу инерции;

На участке «СЕ» действует равномерно распределенная нагрузка интенсивностью:

индекс «max» для простоты записи опущен.

Участок EL нагружен аналогично тому, как нагружен стержень. Согласно эпюре q(z), см. рис. 17.4, суммарная сила инерции будет равна: 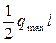, или, опуская для простоты записи индекс «max», можем записать:

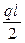
Точка приложения этой силы на участке EL Me имеет значения, так как на самом участке EL она изгибающего момента создавать не будет.

Все силы инерции направляются в сторону от оси вращения «AB».

2. Эпюра изгибающих моментов.

В первую очередь необходимо определить реакции в шарнирах. В настоящем случае имеет место системы параллельных сил. Составим два уравнения равновесия моментов относительно точек «А» и «В». Проверкой будет уравнение суммы сил на вертикаль.

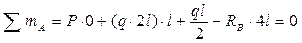
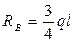
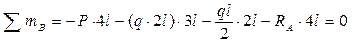
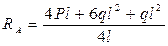
Проверка:

;

;

;

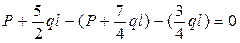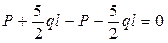0=0.

Положительные знаки реакции указывают на то, что мы «угадали» их направления.

Построение эпюры осуществим по участкам.

1-ый участок СЕ. 0≤z₁≤2l.

Слева от сечения:

.

При z₁=0,M_X (c)=0; при z₁=2l,

Ординаты откладываем в положительную сторону оси Y₁

Эпюра параболическая. В сечении «С» поперечная сила не равна нулю, значит экстремума нет. Кривизна эпюры: q>0, то есть выпуклостью вниз.

Строим эпюру M_X (z₁), см. рис. 8.18

2-ой участок LЕ. 0≤z₂≤l

Сверху от сечения:

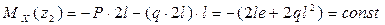
Откладываем ординаты против направления оси Y₂. Строим эпюру M_X (z₂), см. рис. 17.8

Рис. 17.8

3-ий участок AL. 0≤z₃≤2l

Слева от сечения:

При z₃=0, M_X (А)=0; z₃=2l .

Эпюра линейная, ординаты откладываем против положительного направления оси Y₃.

Строим эпюру M_X (z₃), см. рис. 17.8

4-ый участок ВL. 0≤z₄≤2l

На четвертом участке удобнее вести отсчет от сечения «В» к сечению «L». Соответственно направлены координатные оси на этом участке, см. рис. 17.7.

Справа от сечения:

При z₄=0, M_X (В)=0; z₃=2l .

Эпюра линейная, координаты откладываем в сторону положительного направления оси Y₄. Строим эпюру M_X (z₄), см. рис. 8.1.8

3. Из построенной эпюры M_X (z) следует, что опасным, то есть расчетным является сечение «L» участка «AL».

.

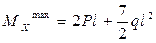Уравнение прочности:

В выражение изгибающего момента в конечном итоге входит угловая скорость. Определяем допускаемое значение изгибающего момента:
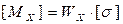, или

Выразим величины [P] и [q] через допускаемую угловую скорость:
.

Учитывая, что:

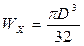и 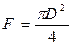, можем записать:

.

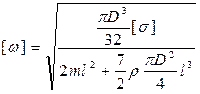Подставляя значения заданных величин с учетом масштабных коэффициентов, получим:

.

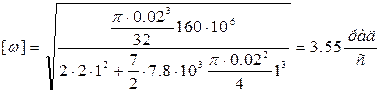Допускаемое число оборотов в минуту:

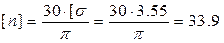об/мин.

Дата добавления: 2015-06-30