Расчёт троса подъёмного механизма

Учёт сил инерции.

В качестве простейшего примера применения принципа Даламбера рассмотрим расчёт троса подъёмного механизма при начале его движения. Схема механизма дана на рис.17.1

Рис. 17.1

При неподвижном грузе на трос действует статическая сила:
..

При подъёме груза в начале движения со скоростью «V» груз испытывает ускорение «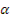», в результате чего возникает действующая сила инерции:

.

Согласно принципу Даламбера эта сила направлена противоположно ускорению, то есть вниз. См. рис. 17.1.

Расчётная схема для троса, как растягиваемого стержня, представлена на рис 17.2. Трос разделён плоскостью «mn», мысленно отброшена верхняя часть.

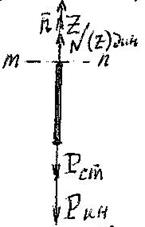
Рис. 17.2

Для оставшейся нижней части составляем уравнение равновесия:

= N – – = 0

Так как внутренний силовой фактор возникает в данном случае при динамическом воздействии, то и нормальная сила является динамической:

N =

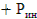
N = ),

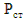
Или: N = ),

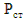
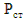
Окончательно: N = ), (17.1)

Разделим уравнение (17.1) на площадь сечения троса:

=

Где и - соответственно динамическое и статическое напряжения, действующие на трос.

При динамическом воздействии иногда удаётся определить динамические коэффициенты. В нашем случае в качестве динамического коэффициента можно принять выражение:

= ,

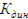Где знак «минус» соответствует опусканию груза.

Тогда окончательно получаем:

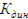
= (17.2)

Статическое напряжение определяется по известной формуле:

= ,

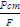а динамическое напряжение получат своё значение в зависимости от значения «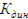». Например, если трос оборвётся, груз будет падать с ускорением, равном «g», динамический коэффициент:

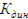= = 0

то есть в тросе при этом напряжения отсутствуют.

Дата добавления: 2015-06-30