Влияние способов закрепления концов стержня на величину критической силы

Формула Эйлера для определения критической силы получила применение в XIX веке при расчете ферм железнодорожных мостов для сжатых поясов и стоек. При этом оказалось, что наряду с удовлетворительными результатами имели случаи конструкций с выпучиванием стержней, что приводило к большим железнодорожным катастрофам.

Было выдвинуто предположение, что так как шарниры в фермах мостов не являются идеальными, необходимо исследовать влияние других способов закрепления концов стержня на величину критической силы.

Были рассмотрены решения дифференциального уравнения упругой линии балки для различных форм закрепления. В нашем курсе удобнее рассмотреть влияние способов закрепления с помощью привидения конфигураций упругой линии балки и основному способу, рассмотренному Эйлером, то есть к полусинусоиде.

На рис. 12.3. показано для каких длин стержней выполняется полусинусоида при различных способах закрепления.

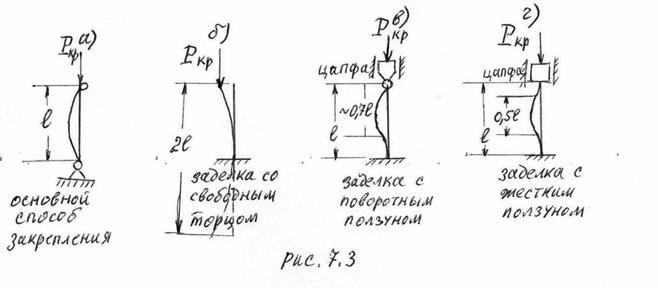
Случай «а)», полусинусоида на всей длине стержня,

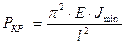
Случай «б)», полусинусоида на двойной длине стержня,

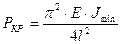
Случай «в)», полусинусоида на части длины стержня, равной ≈ 0,7 длина стержня. Подставив этот коэффициент в основную формулу, получим:

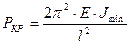
Случай «г)», полусинусоида на половине длины стержня,

В общем виде окончательно выражение критической силы по Эйлеру записывается в следующем виде:

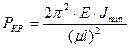(12.15)

Где µ - коэффициент приведения длины.

Для рассмотренных случаев закрепления концов стержня коэффициенты приведения длины имеют следующие значения:

а) µ=1

б) µ=2

в)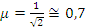

Дата добавления: 2015-06-30